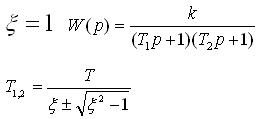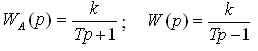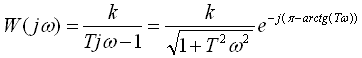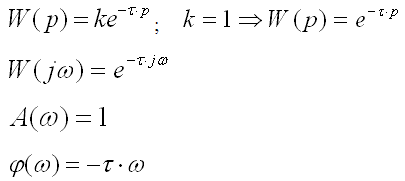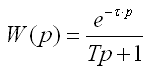| Лекции по ТАУ | Методические указания | Программные средства | Контрольные вопросы | Тестирование | Дополнительно |
3.1. Временные характеристики. Понятие детерминированных и стационарных САУ. 3.1. Временные характеристики. Понятие детерминированных и стационарных САУ. Рассмотрим систему с одним входом и выходом. Предположим, что система не содержит каких-либо независимых источников энергии и предварительно (до подачи входного сигнала) не возбуждена, т.е. находится при нулевых начальных условиях.
Данное уравнение это не что иное, как лаконичное утверждение о существовании причинно-следственной связи между x и y. Система называется детерминированной, если каждому входному сигналу x(t) отвечает один единственный сигнал y(t). В недетерминированных системах входному сигналу могут соответствовать несколько возможных выходных сигналов, каждый из которых имеет определенную вероятность появления. Входные воздействия x(t) могут также быть как известными, так и случайными функциями. Система называется стационарной, если взаимосвязь между входом и выходом не зависит от времени.
В стационарной системе величина и вид выходного сигнала не зависит от момента приложения входного воздействия. Временные характеристики вводятся в ТАУ с целью изучения поведения автоматических систем во временной области, когда о свойствах элемента или системы можно судить на любом этапе управления по его реакции на поступающее воздействие. В принципе, эту реакцию можно найти, решив ДУ. Однако для практических систем сделать это трудно по двум причинам: 1) порядок уравнения в реальных системах обычно высокий; 2) воздействия, входящие в правую часть уравнения или сложные или случайные функции времени. В таких условиях решить ДУ, даже если оно линейное, трудно. Если же воздействие будет представлять собой простейшую аналитическую функцию, для которой ДУ легко решить, то задача исследования существенно упрощается. Это особенно удобно для типовых звеньев и их простейших соединений, описываемых уравнениями не выше 2-го порядка. В качестве воздействия такого типа в ТАУ используют специальные функции, которые определяют временные характеристики.
3.2. Специальные функции. Специальными функциями называется класс функций, составляющих основу временного анализа систем и объектов управления. Каждая специальная функция и ее производные являются непрерывными функциями времени при всех, кроме одного, действительных значениях времени. Далее специальные функции могут быть получены одна из другой последовательным дифференцированием или интегрированием.
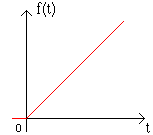
Интегрируя ее можно получить другие специальные функции.
3) Единичная параболическая:
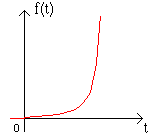
Продолжая многократное интегрирование, можно получить функции 3-го, 4-го и т.д. порядка, также встречающиеся в практике эксплуатации САУ. Реакция системы на единичное внешнее воздействие называется переходной функцией (характеристикой). Обозначается она обычно h(t).
Характеристики Если взять определенный интеграл вида Функцию, описывающую реакцию системы на единичное импульсное воздействие при нулевых начальных условиях называют импульсной переходной или весовой функцией (функция веса системы) w(t). Весовая функция имеет фундаментальное значение для анализа САУ. Если задана весовая функция, то определена вся информация о динамических свойствах системы. Рассмотрев понятие
В таблице (Т-3.1) сведены некоторые специальные функции и их изображения по Лапласу: Таблица 3.1
3.3. Временные характеристики типовых звеньев. Временными характеристиками называют переходную и импульсно - переходную характеристики. Временные характеристики типовых элементарных звеньев сведены в таблице (T-3.2). Таблица 3.2.
3.4. Частотные характеристики линейных динамических звеньев и систем. Наряду с преобразованием Лапласа для математического описания, преобразования и исследования линейных динамических звеньев и систем используется преобразование Фурье, которое можно рассматривать как частный случай преобразования Лапласа, когда произвольная абстрактная независимая переменная p рассматривается как мнимая конкретная переменная
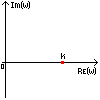
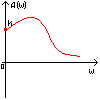
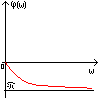
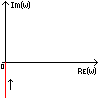
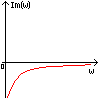
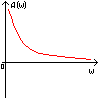
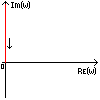
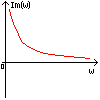
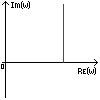
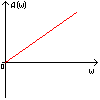
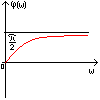
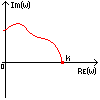
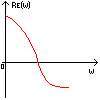
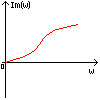
Полученная функция комплексной переменной называется частотной передаточной функцией или частотной функцией звена. Для удобства исследования частотных характеристик звеньев используют их графические изображения, представленные на рис. 3.4.1. Наиболее общее частотной характеристикой (ЧХ) ДЗ является так называемая амплитудно-фазовая частотная характеристика (АФЧХ), которая строится на комплексной плоскости таким образом: по оси абсцисс откладывается действительная часть ФКП (функции комплексной переменной), а по оси ординат - мнимая часть ФКП. Таким образом, чтобы построить график АФЧХ, необходимо функцию комплексной переменной разделить на вещественную и мнимую части, т.е. получить выражение в алгебраической форме:
где
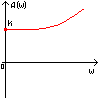
где A(w) = |W(jw)| - амплитуда или амплитудно-частотная функция (АЧХ - ее график);
где Между показательной и алгебраической формой представления частотной ПФ существует взаимосвязь в виде выражений:
Если теперь изменять w от 0 до
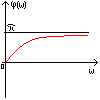
рис. 3.4.1. Частотные характеристики. Можно получить выражение для
Т.е. для любого ДЗ может быть построены и исследованы частотные характеристики по следующей схеме:
Из вышесказанного ясно, что анализу подвергаются пять частотных характеристик АФЧХ, ВЧХ, МЧХ, АЧХ и ФЧХ. Следует отметить, что ЧХ не являются чисто математической абстракцией. Физический смысл ЧХ удобно показать на примере линейной стационарной системы.
Если на вход подать гармонический сигнал вида:
и взять одну из его составляющих и положить то на выходе также установятся гармонические колебания вида
Если
т.к. обычно выходной сигнал отстает от входного. Любую ЧХ линейного звена можно получить экспериментально, подавая ему на вход гармонические воздействия различной частоты; дожидаясь установления выходного сигнала (переходный процесс закончился) ОУ или ДЗ, и фиксируя отношение входного и выходного сигналов, и разности их фаз, как функции частоты. На этом свойстве линейных ДЗ основываются экспериментальные методы математического анализа по схеме:
3.5. Частотные характеристики типовых звеньев. Пять основных частотных характеристик для типовых ДЗ показаны в таблице (T-3.3). Таблица 3.3. (Т-3.3.)
3.6. Логарифмические частотные характеристики динамических звеньев. Кроме перечисленных ЧХ используют еще и ЛЧХ, логарифмические ЧХ ( ЛАЧХ и ЛФЧХ). Ввиду особой важности при исследовании систем и звеньев САУ рассмотрим понятие ЛАЧХ и ЛФЧХ более подробно.
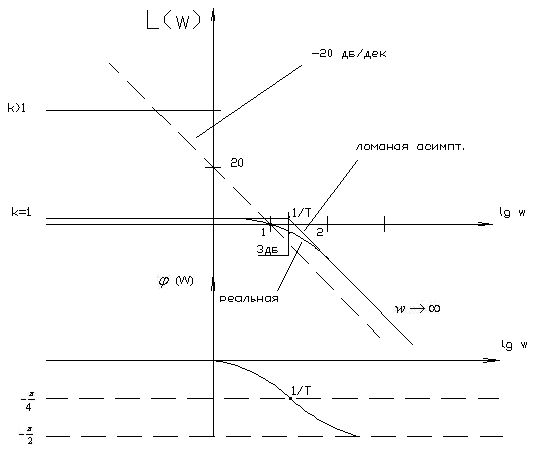
График зависимости логарифма амплитуды от логарифма частоты называют логарифмической АЧХ.
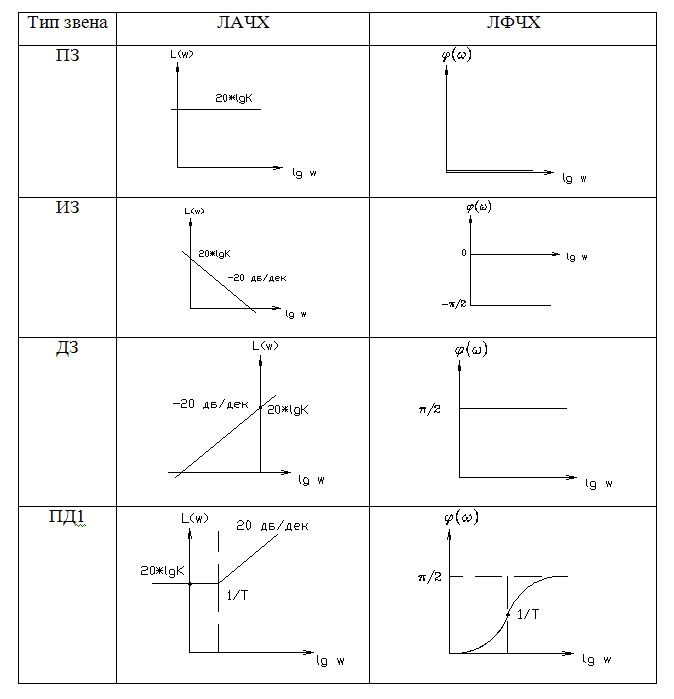
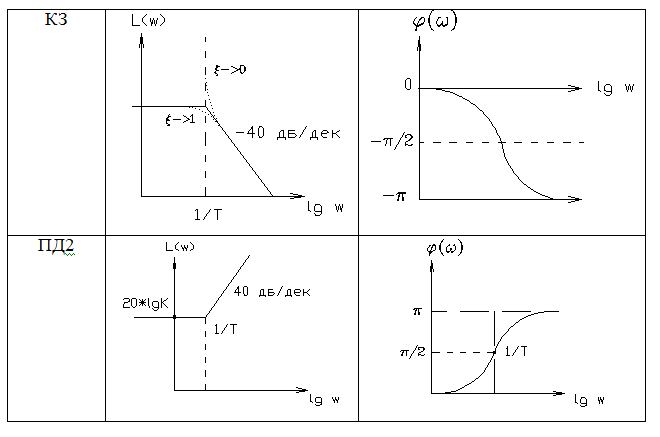
По сопрягающей частоте можно построить ЛЧХ. Реальную ЛАЧХ можно заменить асимптотической, для удобства построения. ЛЧХ сохраняет свою форму при изменении t, но если изменяется Для построения ЛЧХ сложных звеньев необходимо рассмотреть ЛЧХ для типовых звеньев. 3.6.1. Логарифмические ЧХ типовых звеньев. В таблице (T-3.4) представлены ЛЧХ для всех ТЗ рассмотренных ранее. Таблица (T-3.4.)
Все звенья первого порядка имеют наклон в 20 дб/дк в зависимости от того, где стоит полином: в числителе или знаменателе, наклон + или – соответственно. Все звенья второго порядка имеют наклон в 40 дб/дк т.е. в 2 раза больше, наклон определяется также. 3.7. Построение ЛЧХ сложных ДЗ. Исходными данными для построения этих характеристик является передаточная функция объекта или системы преобразуемая к канонической, последовательно-структурированной форме записи:
При построении ЛФЧХ сложного ДЗ, особенно при приблизительных инженерных расчетах, удобно построить все ЛФЧХ типовых звеньев и графически их сложить, т.к. все эти характеристики типовые и меняют только положение относительно оси абсцисс (согласно частоты сопряжения). При построении ЛАЧХ сложных ДЗ процедура графического сложения необязательна и неэффективна с временной точки зрения, т.к. возможно последовательное построение графика асимптотической характеристики путем поворота асимптот в сопрягающих частотах при движении по оси частот слева направо. 3.7.1. Правило построения низкочастотной асимптоты ЛАЧХ.
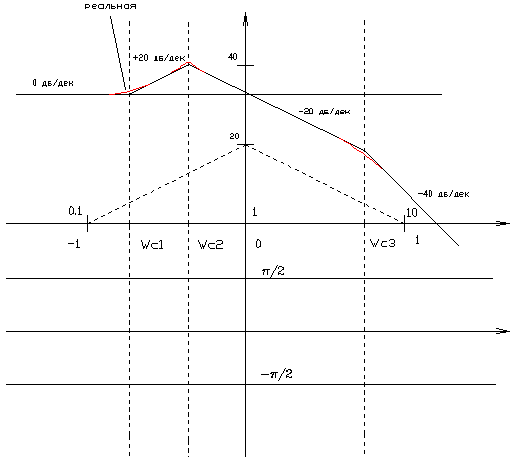
Таким образом на оси частот откладывается точка соответствующая нуля, на оси ординат откладывается 20lg(k) и через эту точку проводится линия с наклоном 20(μ-ν). 3.7.2. Правило построения среднечастотной асимптоты ЛАЧХ. Определяется сопрягающие частоты всех элементарных звеньев входящих в сложное; они располагаются на оси частот в порядке возрастания, через эти частоты проводятся ординаты пунктиром. Построенная низкочастотная асимптота проводится до точки пересечения с первой ординатой – это будет первая точка поворота ЛАЧХ. Далее определяется звено, которое соответствует этой частоте и в соответствии с его характеристиками изменяется наклон ЛАЧХ сложного звена; она продолжается до точки пересечения со следующей ординатой. 3.7.3. Правило построения высокочастотной асимптоты ЛАЧХ. Последняя построенная асимптота продолжается до бесконечности. 3.7.4. Пример.
3.8. Нетиповые динамические звенья. Нетиповые звенья получены на основе типовых. а) Резонансное (консервативное):
б) Апериодическое второго порядка:
в) Нелинейно-фазовые звенья.
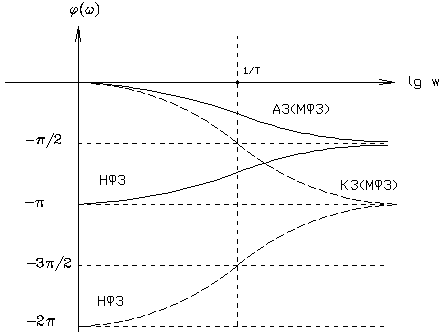
В минимально-фазовых звеньях, т.е. типовых, есть однозначная связь между АЧХ и ФЧХ, т.е. для полной идентификации 4 характеристик достаточно знать только одну из них. Пример:
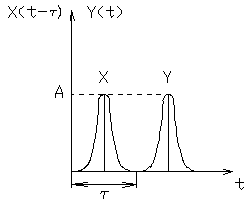
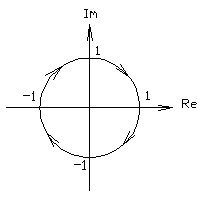
г) Нетиповые звенья, описываемые трансцендентной функцией (звено чистого запаздывания). Звено чистого запаздывания - такое звено, в котором величина на выходе воспроизводит без искажений изменение величины на входе, но с некоторым постоянным запаздыванием. Явным примером звена чистого запаздывания является конвейер.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
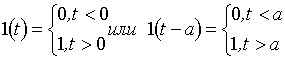
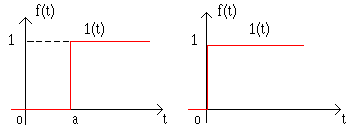
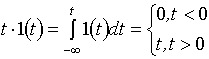
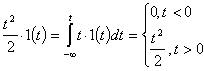
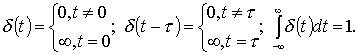
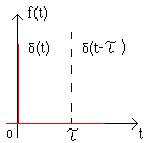
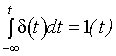 то видно, что из
то видно, что из 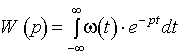 (3.1)
(3.1) 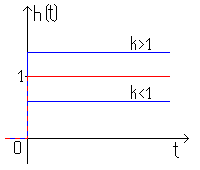
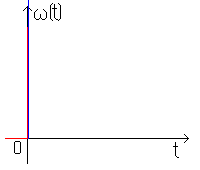
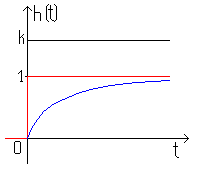
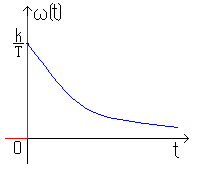
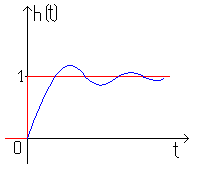
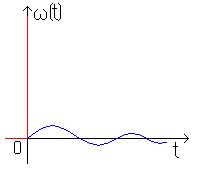
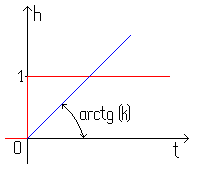
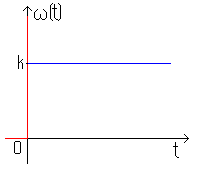
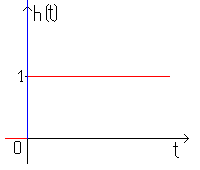
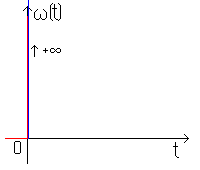
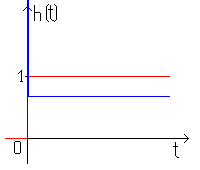
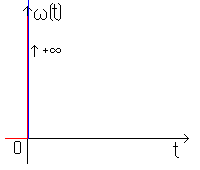
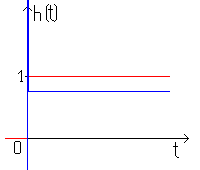
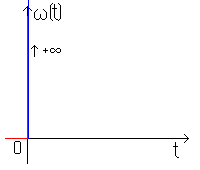
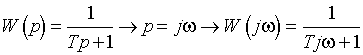
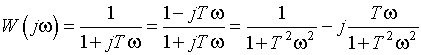
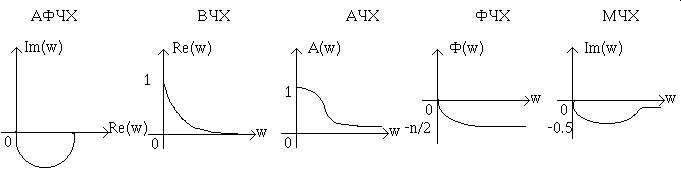
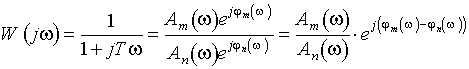
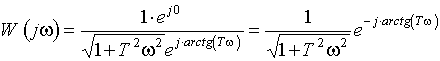

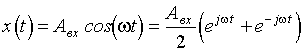
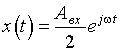
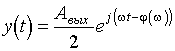 тогда
тогда 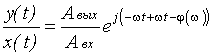
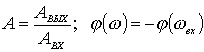
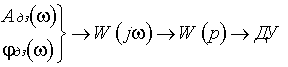
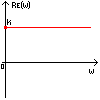
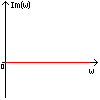
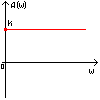
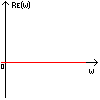
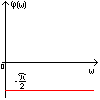
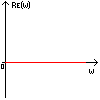
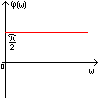
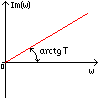
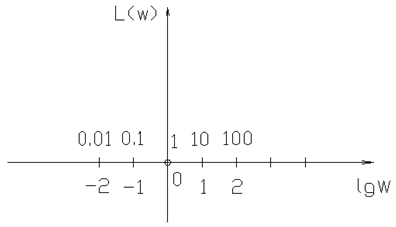 (3.5)
(3.5) 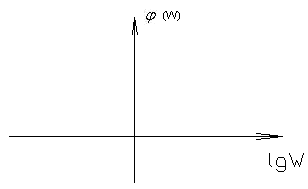
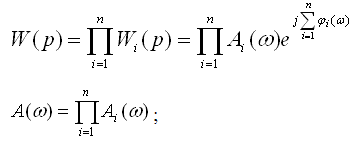
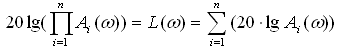
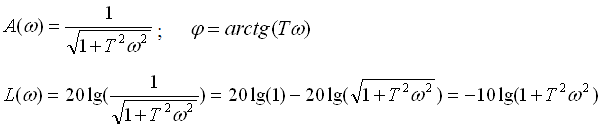
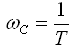 Сопрягающая частота:
Сопрягающая частота: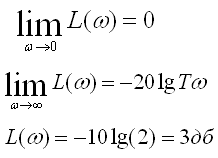
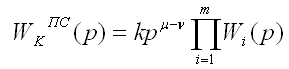
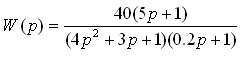
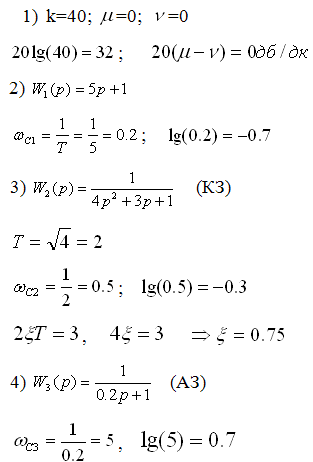
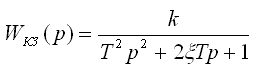 можно получить:
можно получить: