| Лекции по ТАУ | Методические указания | Программные средства | Контрольные вопросы | Тестирование | Дополнительно |
2. Описание объектов и систем управления.
2.1. Формы представления математических моделей. 2.1. Формы представления математических моделей. Пример.
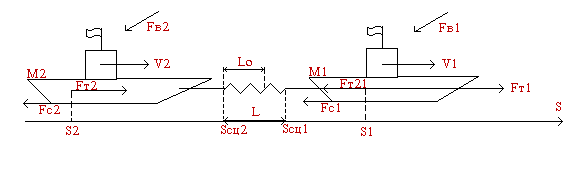
рис. 2.1.1. Система управления. FT1 - сила тяги;
где C - жесткость сцепки. Сила сопротивления воде буксира находится по выражению Тогда зная, что
Из рисунка видно, что тогда Перейдем, теперь, от системы 4-х ДУ к 1-му ДУ, для этого продифференцируем два последних уравнения в системе, получим
преобразуем ее к виду
выразим из второго уравнения
найдем его производные
Вывод: при получении математического описания данного объекта управления был последовательно получен ряд форм моделей от системы 4-х уравнений 1-го порядка до одного уравнения 4-го порядка. Форма (II.1) содержала 4 переменных состояния: v1, v2, s1, s2, которые при сделанных допущениях полностью описывали в каждый момент времени состояние механической системы. Форма ММ (II.2) получена путем исключения ряда переменных состояний и приведения к одному ДУ, разрешенному относительно одной интересующей нас переменной, являющейся одновременно и управляемой (выходом объекта). При этом в модели сохраняются все входные воздействия, которые были учтены в исходной системе. Эта форма описания менее полная, чем исходная, но облегчает и упрощает многие преобразования и анализ. Ее используют тогда, когда задача управления допускает формирование законов управления (ЗУ) при неполной информации о состоянии объекта. Теория управления пережила 2 этапа: классическая теория, которая работала с вход-выходными моделями объекта, и современная теория управления (60-е годы XX века), которая работала с уравнениями состояния. 2.2. Математическое описание объектов и систем управления.
Таким образом, целью исследования и преобразования в ТАУ являются ММ объектов и систем. ММ реального технического устройства - есть его математический образ (МО). Математической моделью является выражение или система выражений, в которых буквенными символами обозначены реальные физические переменные, изменяющиеся в процессе функционирования объекта, а символами математических операций отображаются реальные физические законы преобразования этих переменных в объекте. В результате изменение состояния переменных в реальном устройстве и решение ММ этого устройства должны давать численно совпадающие результаты. Степень совпадения этих результатов указывает на степень адекватности ММ ее техническому оригиналу. Первым этапом решения задачи ТАУ, как вы уже поняли из примера, является получение ММ элементов и звеньев объекта или системы. Последующие этапы сводятся к преобразованию и анализу этих моделей. Существуют различные радиально отличающиеся формы представления моделей. Наиболее общей, полной и естественной формой описания любых явлений природы является дифференциальная (см. пример. - форма II.1), когда ММ представляется в виде системы ДУ. Основной трудностью использования этой формы описания является сложность и громоздкость решения ДУ, особенно нелинейных, и в частных производных. А подавляющее большинство технических объектов описывается нелинейными ДУ и уравнениями в частных производных, так как процессы в них развиваются и во времени и в пространстве. Однако трудности с которыми сталкиваются при их изучении заставляют упрощать эти ММ, если это допустимо. Самым распространенным способом упрощения ММ является линеаризация, так как для линейных ДУ в математике и для линейных объектов в ТАУ существуют хорошо развитые операторные методы. Для осуществления операции линеаризации необходимо, чтобы линеаризуемая функция была дифференцируема на всем протяжении (не имела разрывы и неоднозначности). Тогда ее можно разложить в ряд Тейлора в окрестности произвольно выбранной точки (для САУ - это обычно положение равновесия Разложение осуществляется по формуле:
где Ф - сумма членов, которые содержат различные произведения отклонений и отклонений во второй и более высших степенях с коэффициентами в виде смешанных частных производных (ЧП) и ЧП второго и высших порядков от функции
2.3.1. Математическое описание одномерных объектов и систем. Исследованиями установлено, что любой линейный динамический объект или система может быть приведен к вход-выходной форме описания. Тогда его математическая модель представляется одним или несколькими дифференциональными уравнениями, выходными переменными которых являются внутренние переменные объекта или системы, называемые выходами. В правых частях этих уравнений будут в общем случае дифференциональные операторы от входных воздействий (как управляющих, так и возмущающих).
где В выражении (2.3) коэффициенты Как отмечалось ранее, при исследовании линейных систем широко применяются так называемые операторные методы. Сущность методов - операции дифференцирования и интегрирования заменяются алгебраическими операциями умножения и деления за счет применения специальных преобразований, что резко упрощает все процедуры преобразования и исследования ММ объекта. Из операторных методов наиболее известны использующие преобразования Лапласа и Фурье, рассмотрим их: 1) преобразование Лапласа
2) преобразование Фурье (для получения частотных характеристик)
При применении операторных методов имеют обычно дело не с абсолютными значениями переменных, а с их, так называемыми, приращениями. Это связано с несколькими причинами: 1) работа большинства автоматических систем протекает в узкой области изменения переменных допускаемой технологии. Существует при этом номинальное уравнение как выходной переменной, так и входных воздействий. y0, v10, v20, а для управления важно знать отклонение переменной от номинального значения
Будем считать, что уравнение (II.3) было записано в приращениях
Тогда к нему можно применить преобразование Лапласа (к правой и левой части) и с учетом нулевых начальных условий по переменным и их производным, получить:
где p - оператор Лапласа, а под Тогда можно получить выражение изображения в следующем виде:
где A(p) - степенной полином вида Рассмотрим случай одного входа:
где W(p) - передаточная функция (ПФ). В случае, если объект описывается ДУ с одним входом и одним выходом, его динамические свойства можно представить не только дифференциальным уравнением, но и передаточной функцией:
Поскольку оказывается, что отношение изображения по Лапласу выходного сигнала к входному при нулевых начальных условиях не зависит от сигналов, т.е. является инвариантом, то ясно, что ПФ является ММ данного объекта. ОПРЕДЕЛЕНИЕ: передаточной функцией динамического звена по каналу z - y, т.е. по каналу воздействия переменной z - входного воздействия и выходной переменной - y, называют отношение изображения по Лапласу исследуемых выходных и входных переменных при условии равенства нулю всех остальных воздействий звена и начальных условий по исследуемым переменным. Если имеется линейное звено с несколькими входами и одним выходом, то оно в операторной области характеризуется несколькими ПФ по каналам воздействия каждого входа на выход. 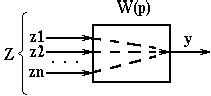 При аналитическом или экспериментальном исследовании этого звена каждая из передаточных функций определяется отдельно. При этом предполагается, что другие входы равны нулю.
После получения передаточных функций по каналам, динамические свойства звена записываются в виде:
где Выражение (2.10) справедливо для любого количества входов (для 1-выходных систем). Аналогичные свойства распространяются на динамические звенья с несколькими выходами:
При этом ДЗ имеет несколько ПФ, количество которых равно числу выходов
2.3.2. Свойства передаточной функции динамического звена. Приведенная и каноническая формы записи. Свойства передаточной функции динамического звена: 1. ПФ линейного звена является дробно - рациональной, т.е. отношением полиномов (многочленов) от комплексной переменной p(s). 2. Порядок полинома в числителе не должен превышать порядок полинома в знаменателе для реального ДЗ. 3. ПФ звена по каналам для одной и той же выходной переменной имеет в знаменателе один и тот же полином. Для звена с одним выходом этот полином является характеристическим полиномом (ХП), т.к. его структура и параметры определяются фундаментальными свойствами ДЗ, прежде всего, его устойчивостью. ПФ представляет собой одну из форм задания ММ ДЗ. Она существует только для линейных ДЗ. Из ПФ могут быть получены другие формы описания, как например, матрично - векторное описание, частотные характеристики и другие. Свойства полиномов числителя и знаменателя передаточной функции: Общий вид полинома:
где Таким образом, сложное ДЗ можно разбить на элементарные звенья. Корни могут быть как вещественные, так и комплексно - сопряженные.
Тогда
где
Таким образом, на элементарные полиномы можно разложить и числитель и знаменатель ПФ и перейти к виду:
где Форма записи ПФ вида (II.14) называется приведенной. Ее можно предствить и в другом виде (без нахождения корней полиномов):
Формы (2.14, 2.15) одни из основных, используемых для исследования сложных ДЗ. Существует и другая форма записи ПФ - каноническая. Для ее нахождения необходимо:
Для общего случая эту форму можно записать так:
где Форма (2.17) является основной при анализе фундаментальных свойств ДЗ, по ней можно судить о сложности объекта, его структуре (если разложить полиномы числителя и знаменателя на элементарные), коэффициенте усиления, порядке астатизма и т. д. Теперь, по аналогии с элементарным полиномом (полиномом наименьшего порядка), введем понятие элементарной ПФ (ЭПФ). Элементарная ПФ - это ПФ, представленная дробью, содержащей не более одного элементарного полинома Разложение звена на элементарные звенья является очень важным приемом, позволяющим оценить основные свойства сложного ДЗ: коэффициент передачи, дифференцирующие и интегрирующие составляющие и т.д. Кроме того, нахождение корней ХП звена, необходимого для разложения ПФ, позволяет определить свойство звена такое, как его устойчивость или неустойчивость. Чаще всего в автоматике имеют дело с устойчивыми, так называемыми нейтральными ДЗ. Устойчивое ДЗ характеризуется тем, что корни его ХП имеют отрицательную вещественную часть. Элементарные звенья, описываемые элементарными ПФ, подразделяются на идеальные и физически реализуемые. Условием физической реализуемости ДЗ является неравенство: где n - порядок полинома в знаменателе, m - порядок полинома в числителе. 2.4. Элементарные звенья. Элементарные идеальные звенья:
Следует отметить тот факт, что любое сложное ДЗ, описываемое ПФ высокого порядка можно представить произведением элементарных ПФ. 2.4.1. Элементарные типовые динамические звенья. Анализируя форму представления передаточной функции (II.14) можно выделить следующие элементарные ПФ: 2.4.2. Свойства и характеристики типовых звеньев.
где Чтобы получить действительный коэффициент передачи любого ДЗ, необходимо в дифференциальной части уравнения сделать коэффициент, стоящий перед y, единичным. Тогда коэффициент, стоящий при x и будет коэффициентом передачи данного звена. Именно поэтому рассмотренную выше ПФ апериодического звена целесообразно представлять в виде:
где T - характеризует быстродействие данного звена (постоянная времени) равна k - коэффициенту усиления. Таким образом, в качестве типового апериодического звена 1-го порядка целесообразно рассмотреть периодическую функцию вида (k = 1): Аналогично осуществляется преобразование других передаточных функций типовых звеньев. Тогда можно составить табл. (T. 2.1) элементарных звеньев, их ПФ, представленных в более удобной форме и ДУ, соответствующие этим ПФ (k = 1): Таблица 2.1.
Постоянная
2.5. Каноническая последовательно-структурированная форма записи. Теперь, рассмотрев основные типовые звенья, покажем как можно перейти от формы (II.17) к так называемой последовательно-структурированной канонической форме. Для этого необходимо найти корни полиномов A(p), B(p) и представить их в виде произведений элементарных полиномов
где
Подставив формулу (2.18) в (2.17) можно представить ПФ в виде произведения ПФ элементарных типовых звеньев:
где
2.6. Структурные представления и анализ в ТАУ. Структурной схемой в ТАУ называется графическое изображение ММ автоматической системы в виде соединения звеньев. Разбиение сложной ПФ ДЗ на элементарные ПФ соответствующих типовых звеньев не является чисто математическим приемом. Любое устройство или САУ физически или технологически разбивается на совокупность ДЗ невысокого порядка. Переход от реальных элементов САУ к их ММ (ДЗ) позволяет абстрагироваться от физических принципов построения систем, поэтому структурная схема является основой универсальных методов анализа и синтеза САУ. ДЗ в структурных схемах оказываются связанными между собой через входные и выходные переменные, причем в линейных системах эта связь осуществляется только через линейные преобразования, т.е. умножением и сложением. В принципе ММ САУ может быть записана и как система ДУ. Однако такая форма громоздкая и ненаглядная. В связи с этим в автоматике принята своеобразная графо-математическая форма представления (структурные схемы). В структурных схемах переменные представляются стрелками, динамические звенья (ДЗ) прямоугольниками, а математическое изложение сигнала - специальными значками. Графические и структурные символы, принятые в ТАУ, сведены в табл. (T-II.2). В структурной схеме используют два закона чтения схемы: Таблица 2.2.
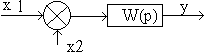
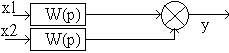
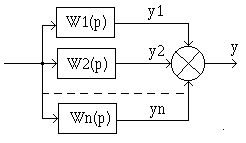
2.6.2. Основные типы соединения звеньев в САУ. 1) Параллельное соединение.
Эта структурная схема преобразуется к виду:
Передаточные функции параллельных звеньев складываются.
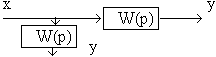
Передаточные функции последовательных звеньев перемножаются.
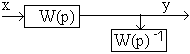
3) Обратная связь..
Для разомкнутой системы общая ПФ:
Для положительной ОС -, для отрицательной ОС +.
ПФ для разомкнутой системы:
2.6.3. Основные правила структурных преобразований. Для получения некоторых эквивалентных ПФ исходной структурной схемы пользуются определенными правилами преобразования. Суть этих преобразований сводится к целенаправленному переносу элементов структурных схем (звеньев, узлов, сумматоров и т.д.) друг через друга, но так, чтобы результирующая ПФ не менялась. В табл. (T-II.3) приведены правила структурных преобразований. Свойства эквивалентных преобразований: Таблица 2.3.
Не всякая структурная схема упрощается до типовой рассмотренными выше методами структурных преобразований. Бывают случаи, когда связь приходится переносить через контур. В этом случае необходимо учитывать ПФ всего контура, а не отдельно взятого звена. В этих случаях применять эквивалентные преобразования не рекомендуется, т.к. проще записать систему алгебраических уравнений для всех звеньев и сумматоров, и затем методом последовательного исключения промежуточных переменных получить эквивалентную ПФ по исследуемому каналу. |
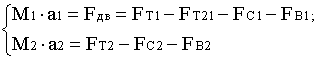
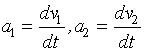 , а
, а 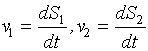 можно переписать систему уравнений в виде
можно переписать систему уравнений в виде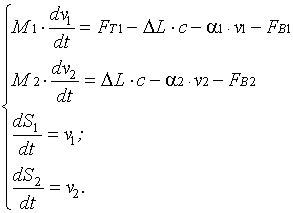 (2.1)
(2.1) 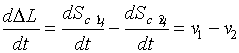
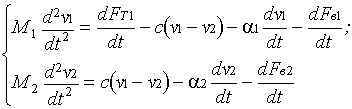
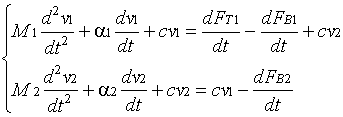
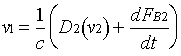
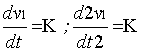 , и подставив их в первое уравнение получим 1 ДУ 4-го порядка вида
, и подставив их в первое уравнение получим 1 ДУ 4-го порядка вида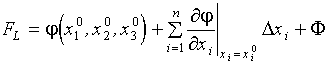
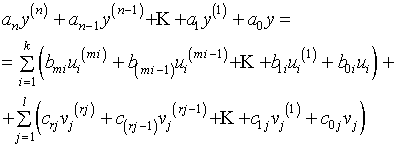 (2.3)
(2.3) 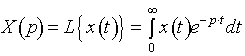 (2.4)
(2.4) 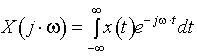 (2.5)
(2.5) 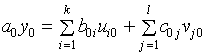 (2.6)
(2.6) 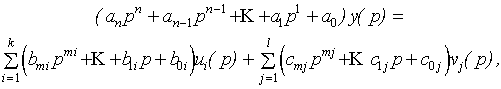 (2.7)
(2.7) 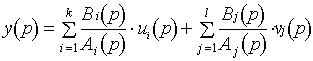 (2.8)
(2.8) 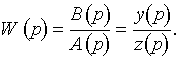 (2.8)
(2.8)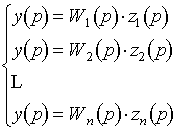
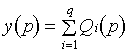 (2.10)
(2.10) 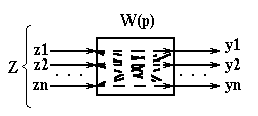
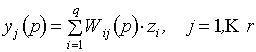 (2.11)
(2.11) 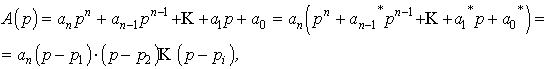 (2.12)
(2.12) 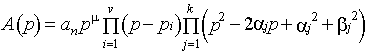 (2.13)
(2.13) 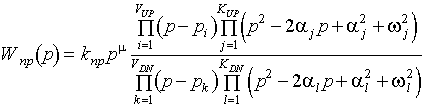 (2.14)
(2.14) 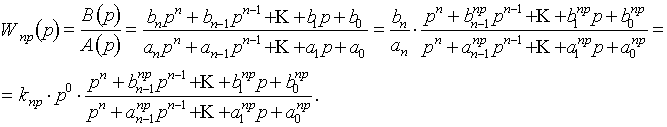 (2.15)
(2.15) 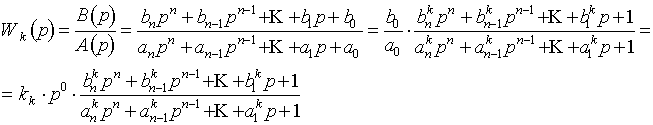 (2.16)
(2.16) 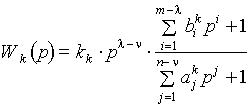 (2.17)
(2.17) 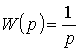 ;
;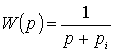 ;
;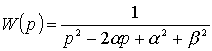 .
.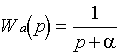 , если
, если 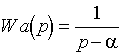 , если
, если 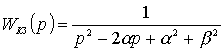 .
.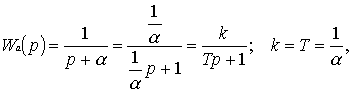
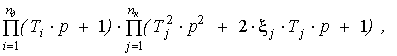 (2.18)
(2.18)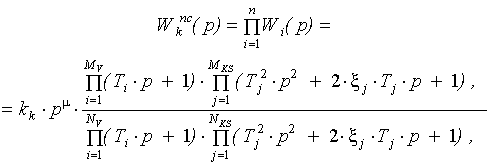 (2.19)
(2.19)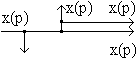
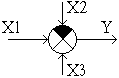
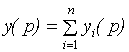
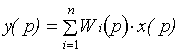 (2.20)
(2.20)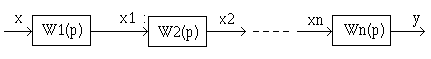
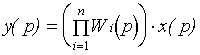 (2.21)
(2.21)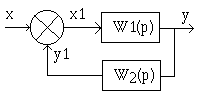
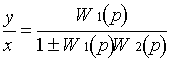
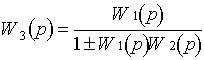 (2.22)
(2.22)