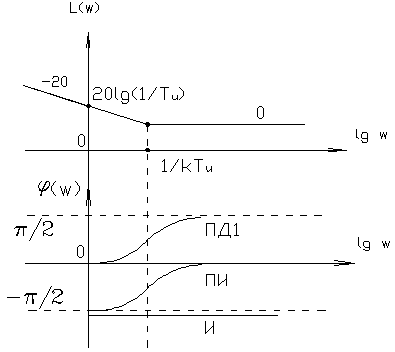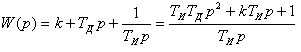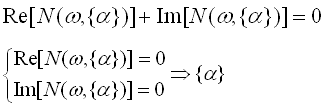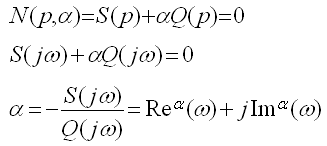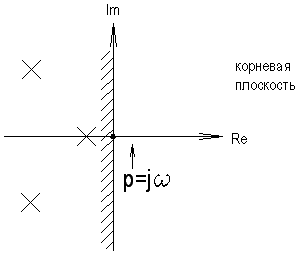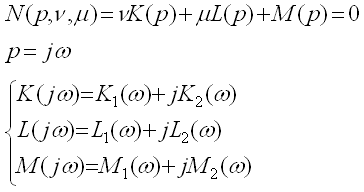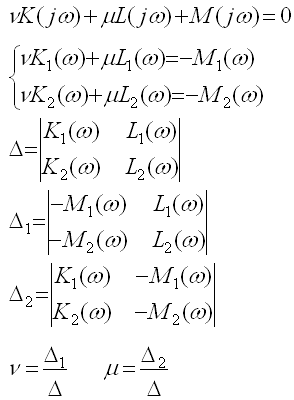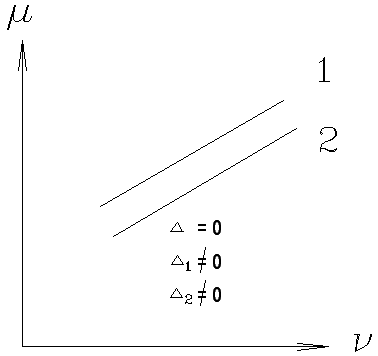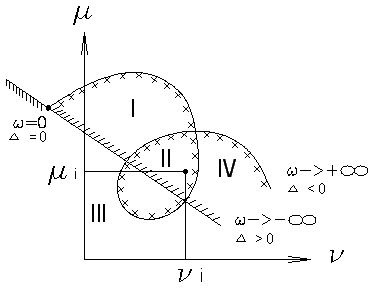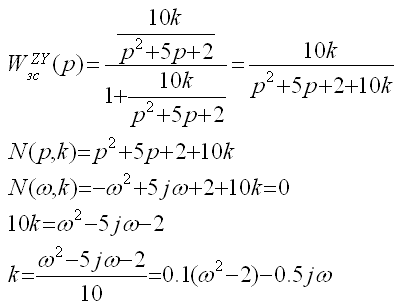| Лекции по ТАУ | Методические указания | Программные средства | Контрольные вопросы | Тестирование | Дополнительно |
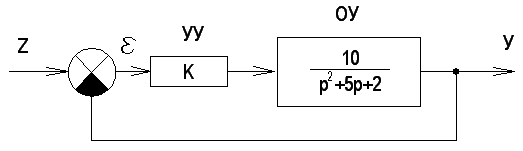
4.1. Структура, математическая модель и основные понятия одноконтурной замкнутой системы. 4.1. Структура, математическая модель и основные понятия одноконтурной замкнутой системы. На рис. (4.1.1) представлена одноконтурная замкнутая система (ЗС).
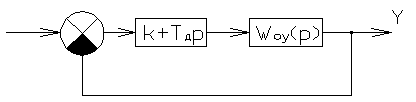
рис. 4.1.1. Одноконтурная замкнутая система. Регулятор - устройство или ДЗ, осуществляющее преобразование ошибки управления в управляющий сигнал. 1. Математическая модель системы по управляющему каналу z-y и z-e:
2. ПФ разомкнутой системы.
где S(p) - ХП разомкнутой системы
Знак ОС в контуре определяется не знаком суммирования в точке ОС, а количеством перемены знака при распространении сигнала по контуру. Если оно нечетное, то ОС "-", если четное - ОС "+". В характеристической функции в числителе стоит характеристический полином замкнутой системы, а в знаменателе характеристический полином разомкнутой системы.
4.2. Устойчивость объектов и систем уравнения.
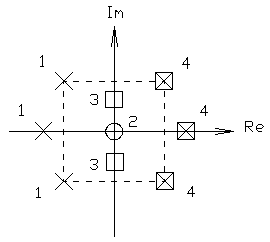
4.2.1. Корневой метод оценки устойчивости (критерий Ляпунова). Для корневой устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического полинома ее передаточной функции имели отрицательные вещественные части.
1 – устойчивые корни 2 – нулевой корень 3 – нейтральные корни 4 – неустойчивые корни 4.2.2. Качественная оценка ХП. Корни, расположенные в левой полуплоскости будем называть устойчивыми, в правой - неустойчивыми, находящиеся на оси - нейтральными. 1) все коэффициенты ХП должны быть одного знака; 2) ХП должен быть полным, т.е. содержать все ненулевые коэффициенты, то есть для каждого Эти же условия для полинома 2-го порядка являются и достаточными. Для ХП более высоких порядков эти условия являются только необходимыми, но не достаточными. Для облегчения анализа устойчивости систем учеными были разработаны критерии, косвенно оценивающие корни ХП без их определения. Использование косвенных критериев существенно облегчает процедуру исследования систем, так как позволяет оценивать их фундаментальные свойства не прибегая к сложным алгоритмам прямого аналитического или численного решения задачи. 4.2.3. Алгебраические методы оценки устойчивости. Алгебраический критерий: 1) В 1878 английский математик Раус предложил критерий:
По критерию Раусса исследуемая система устойчива, если все коэффициенты в первом столбце таблицы Раусса имеют одинаковый знак, если условие не соблюдается, то характеристический полином имеет неустойчивые корни. Количество которых равно числу перемен знака. В таблице всегда (n-1) строк. Правило определения устойчивости: 3) Правило: Если все коэффициенты характеристического полинома равны 0 и все главные миноры матрицы Гурвица с четными (нечетными) номерами тоже, то характеристический полином является устойчивым.
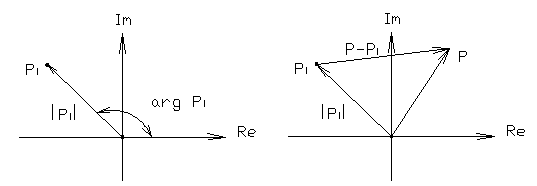
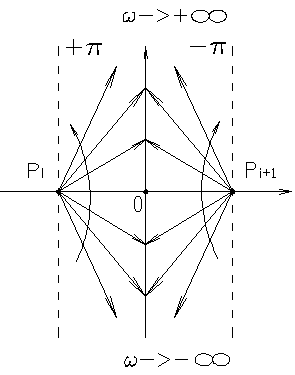
4.2.4. Частотные методы оценки устойчивости. Во всех частотных критериях при оценке устойчивости используют один и тот же принцип, и он называется принципом аргумента.
Для устойчивости объекта или системы необходимо и достаточно, чтобы суммарный угол поворота комплекса характеристического полинома при изменении ω от 0 до ∞ был равен
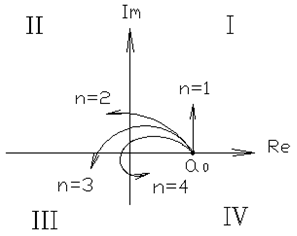
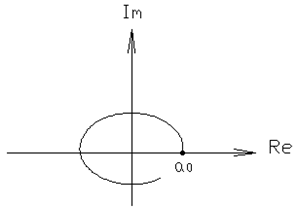
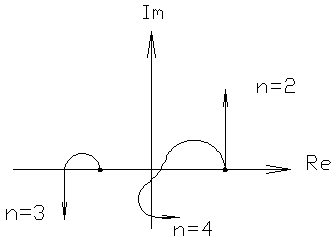
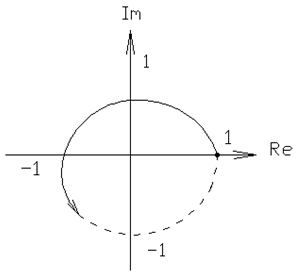
4.2.5. Критерий устойчивости Михайлова. По сути это частный случай принципа аргумента, при оценке удобно использовать графическую интерпретацию последнего, для этого на комплексной плоскости строится кривая, которая вычерчивает вектор характеристического полинома Правило оценки устойчивости: для того, чтобы система была устойчива необходимо и достаточно, чтобы годограф начинался на положительной вещественной оси из точки Пример: Устойчивые
Не устойчивые
На границе устойчивости
4.2.6. Модифицированный критерий Михайлова. Обычно применяется при построении и анализе годографа Михайлова в математических пакетах.
В данном критерии фазовый сдвиг вносимый корнями сохраняется и проходит такое же количество квадрантов как в обычном критерии, а изменяется только модуль, который нормируется в соответствии с коэффициентом стоящим в знаменателе.
4.3. Критерий устойчивости замкнутых систем, основанный на исследовании свойств разомкнутых систем. 4.3.1. Частотный критерий устойчивости Найквиста. Критерий Найквиста (американсткий ученый) был получен и сформулирован в 1932 г. для оценки устойчивости ЗС по частотной характеристике РС. ПФ и ХФ разомкнутой системы:
где L(p)+S(p) - ХП замкнутой системы, а S(p) - ХП разомкнутой системы. При этом
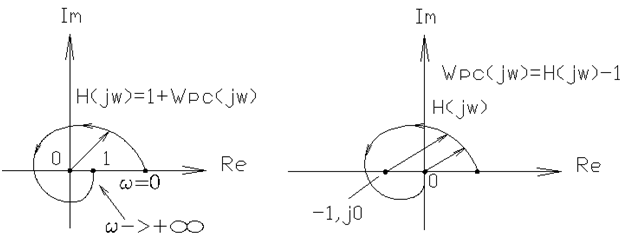
Годограф, изображающий характеристическую функцию совпадает с годографом АФЧХ разомкнутой системы, если начало вектора перенести в точку Таким образом, если из условий устойчивости корней характеристического полинома найти обязательным образом связанные свойства вектора, изображающего характеристическую функцию, то можно по годографу АФЧХ разомкнутой системы судить об устойчивости замкнутой системы. Для оценки устойчивости можно использовать принцип аргумента, как в критерии Михайлова. 4.3.2. Аналитическая трактовка критерия Найквиста.
Пусть в разомкнутой системе в характеристическом полиноме есть r – устойчивых, m – неустойчивых и q – нейтральных корней.
Звенья с нулевыми корнями изменяют фазовую характеристику в процессе изменения частоты, но вносят в первоначальный фазовый сдвиг равный Для того, чтобы замкнутая система была устойчивой необходимо и остаточно, чтобы вектор проведенной из точки 4.3.3. Графическая трактовка критерия Найквиста. Частные случаи применения. 1) Разомкнутая система - устойчивое ДЗ.
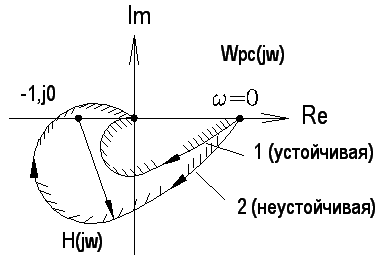
Для устойчивости замкнутой системы необходимо и остаточно, чтобы годограф АФЧХ не охватывал точку с координатами 2) Разомкнутая система - сложное ДЗ с астатизмом 1-го порядка.
1 – устойчива
2 – неустойчива
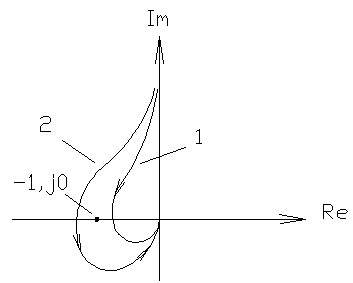
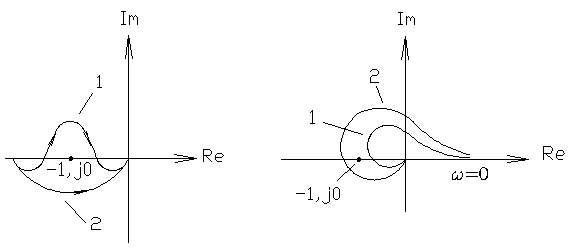
3) Разомкнутая система - сложное ДЗ с астатизмом произвольного порядка (допустим третьего).
1 - неустойчива (-1 попадает в область штриховки),
2 - устойчива (штриховка вне -1).
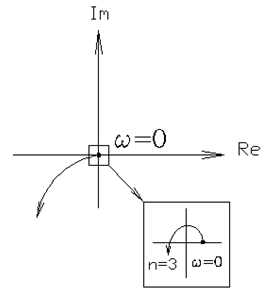
4) Система разомкнутая, содержит неустойчивое звено 1-го порядка (1 неустойчивый корень).
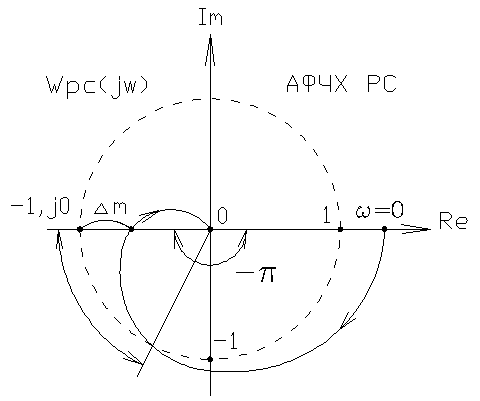
4.4. Понятие запасов устойчивости замкнутой системы. Критерий Найквиста имеет еще одно преимущество по сравнению с рассмотренными выше: с использованием этого критерия, анализируя АФЧХ РС, можно оценить количественно близость устойчивой системы к границе неустойчивости и близость неустойчивой системы к устойчивому состоянию.
рис. 4.8.1. Фазовая плоскость. +
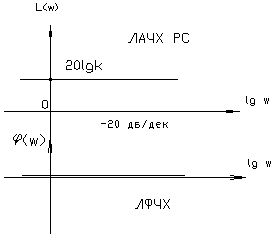
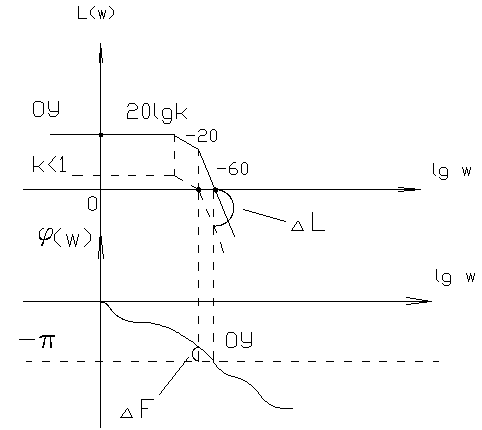
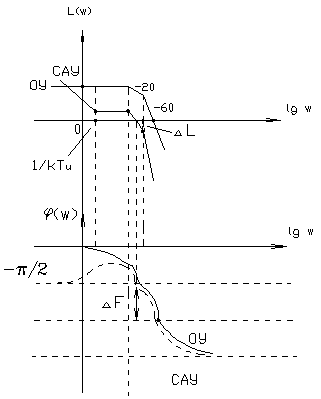
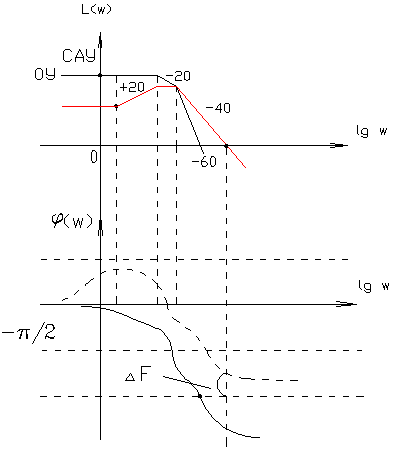
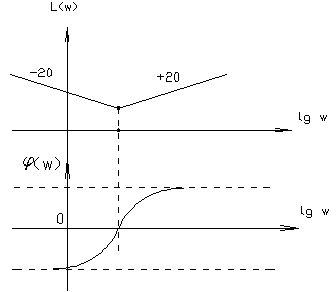
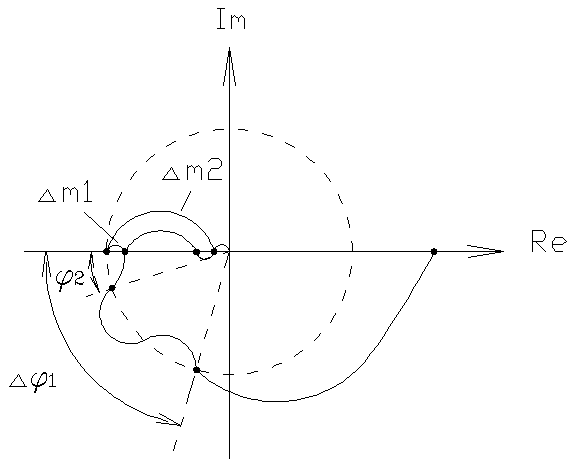
Возможны случаи, когда запасов устойчивости получается несколько, построенных по определению. В этом случае можно рассмотреть всю совокупность запасов или наихудший вариант. 4.4.1. Трактовка критерия Найквиста с использованием ЛЧХ. Применение рассмотренного аналитического и графического критериев Найквиста к ЧХ РС на логарифмической плоскости приводит к более наглядной оценке устойчивости и неустойчивости системы и запасов устойчивости по модулю и фазе. На графиках ЛЧХ запас по фазе определяется в тех же единицах (градусы или радианы), а запас по модулю - в децибеллах.
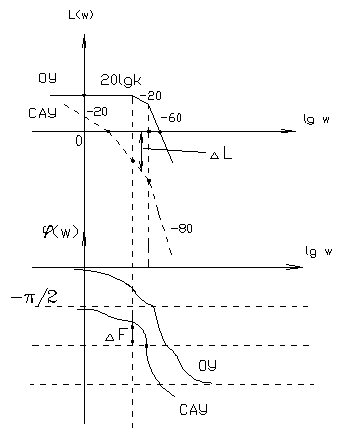
рис. 4.8.2. Критерий Найквиста по ЛЧХ. Формулировка: Замечание: замкнутая система будет однозначно устойчивой, если ЛАЧХ целиком лежит ниже оси 0, а фазовая имеет всплеск над осью В инженерной практике, в процессе проектирования реальных систем управления были выработаны эмпирические оценки и значения запасов устойчивости, обеспечивающих не только устойчивость системы, а и удовлетворительное качество переходных процессов в них протекающих. Связь между качеством системы и значением запасов – не жесткая, но величина запасов зависит от порядка разомкнутой системы и степени ее астатизма. Чем больше порядок астатизма и размерность разомкнутой системы, тем выше запас устойчивости. 4.4.2. Определение запасов устойчивости системы с использованием ЛЧХ. В ежедневной практике выработались эмпирические оценки значений запасов устойчивости, обеспечивающих не только устойчивость системы, но и удовлетворительное качество ПП в ней (степень затухания колебаний, перерегулирования). Чем больше значение запаса устойчивости системы, тем выше качество процессов в ней. Поэтому при использовании критерия Найквиста оценивают не только сам факт устойчивости, но также определяют значения запасов устойчивости и сравнивают с допустимыми значениями. Связь между качеством системы и значением запаса нежесткая, значения запасов зависят от порядка ПФ РС и порядка ее астатизма, а сами значения получены эмпирически. Для каждого типа систем допустимые значения берутся тем выше, чем больше порядок системы и порядок астатизма, что продемонстрировано в таблице (T-4.1): Таблица 4.1.
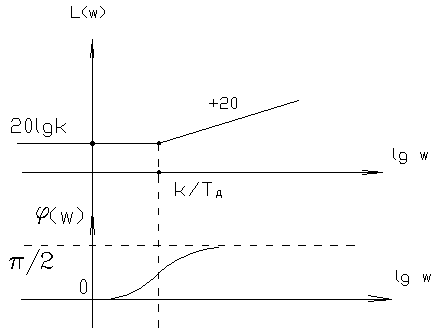
4.5. Синтез систем автоматического управления Существует 5 типовых регуляторов. Среди этих регуляторов есть простые и сложные. 1) П – пропорциональный регулятор, 2) И – интегрирующий регулятор, 3) ПИ – пропорционально интегральный регулятор, 4) ПД - пропорционально дифференциальный регулятор, 5) ПИД – пропорционально интегрально дифференцируемый регулятор, Достоинства и недостатки каждого регулятора:
Достоинство: Недостаток: 2) И – регулятор (применяется для статических систем)
Достоинства: Недостатки: 3) ПИ - регулятор
Достоинства: Недостатки: 4) ПД – регулятор
Достоинства: Недостатки: 5) ПИД – регулятор
4.6. Построение областей устойчивости CАУ в плоскости их параметров. Для построения таких областей применяется метод предложенный Неймарком Ю.И. и названный им метод D-разбиения. Для построения областей устойчивости в плоскости нескольких параметров системы необходимо знать ее ХП N(p):
Далее определяем множество неких численных коэффициентов и приравниваем к нулю ХП. После чего представляем это уравнение в виде:
Наибольшее распространение в инженерной практике получили два вида D-разбиения: по одному и по двум параметрам, так как при использовании большего числа параметров теряется наглядность метода. 4.6.1. Однопараметрическое Д - разбиение. Исходными данными являются характеристический полином замкнутой системы, в котором присутствует один варьируемый параметр.
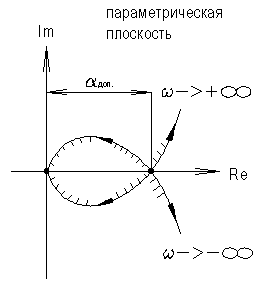
Для определения области устойчивости САУ на параметрическую кривую необходимо нанести штриховку слева по мере увеличения частоты (по аналогии с корневой плоскостью). Примечание: для построения параметрического годографа необязательно изменять частоту от 4.6.2. Двухпараметрическое Д - разбиение. Исходные данные: характеристический полином замкнутой системы, в который входят два варьируемых параметра.
Так как K2, L2 и M2 являются нечетными функциями, то Рассмотрим три возможных случая решения систем уравнений. 1)
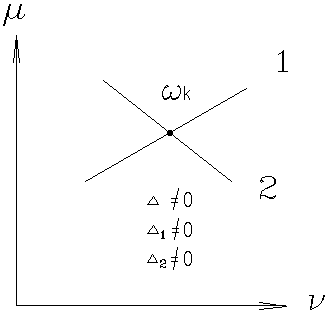
Уравнения совместны и имеют общее решение. 2)
Уравнения несовместны и не имеют общее решение. 3)
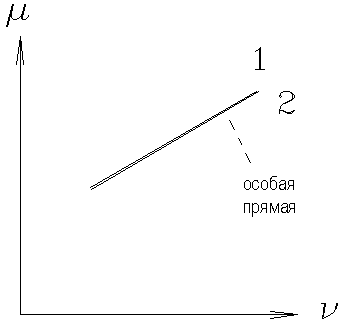
Особая прямая – линия, построенная при одном и том же значении Правила штриховки параметрических кривых и особых прямых. 1. (Для параметрической кривой) При возрастании 2. (Для особых прямых) Штриховка особых прямых, как правило, одинарная и производится так, чтобы в точке сопряжения особой прямой и параметрической кривой заштрихованные стороны кривой и прямой были направлены друг к другу. После нанесения штриховки определяется область, претендующая на область устойчивости.
Области, претендующие на устойчивость – I и II. Область II после проверки будет действительно являться областью устойчивости. При переходе через линию двойной штриховки их заштрихованной области в незаштрихованную два устойчивых корня становятся неустойчивыми. При переходе через линию одинарной штриховки аналогично, неустойчивым становится первый корень. Пример:
|
|||||||||||||||||||||||||||||||||||||||||||||||

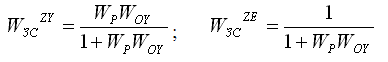
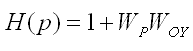 - характеристическая функция
- характеристическая функция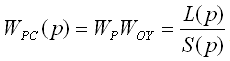
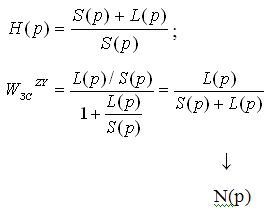
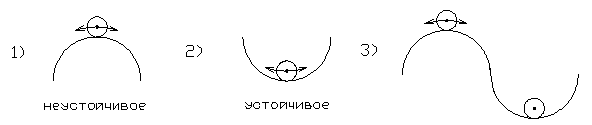
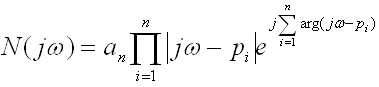
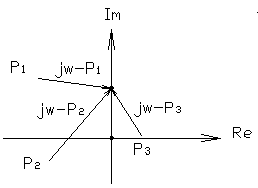
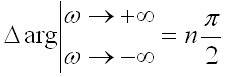
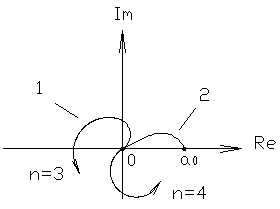
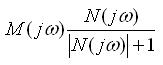
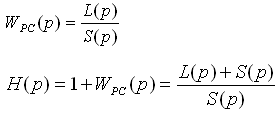
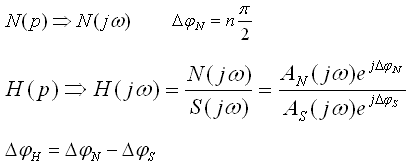
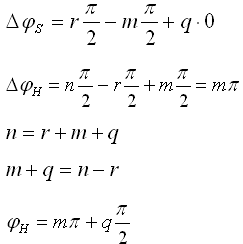
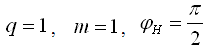
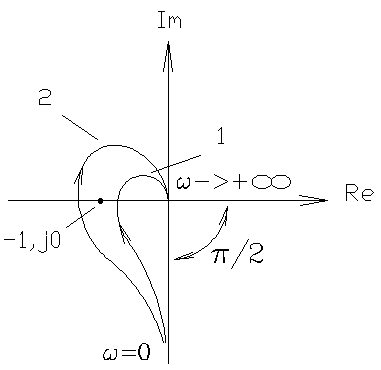
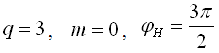
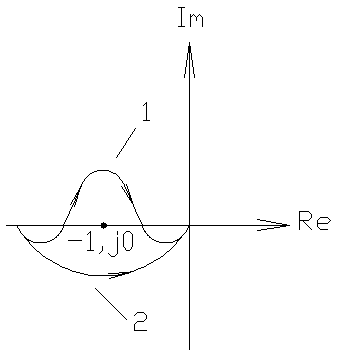
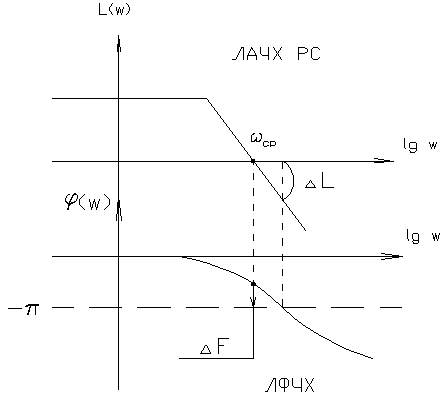
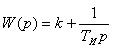 (является сложным и астатическим).
(является сложным и астатическим).