• Нормали. Нормали к плоскости
• Плоскость, перпендикулярная к прямой
• Нормаль к прямой
• Метрические задачи. Задачи на определение величины углов
  • Угол между пересекающимися прямыми
  • Угол между скрещивающимися прямыми
  • Угол между прямой общего положения и плоскостью общего положения
  • Двухгранный угол
• Метрические задачи. Задачи на определение расстояний
  • Расстояние между двумя точками
  • Расстояние от точки до прямой
  • Расстояние между параллельными прямыми
  • Расстояние между параллельными плоскостями общего положения
  • Расстояние между скрещивающимися прямыми
  • Расстояние от точки до поверхности вращения

1. Нормали. Нормали к плоскости

Рис. 326

1. Перпендикуляр (нормаль) к проецирующей плоскости – прямая уровня. Например, к горизонтально проецирующей плоскости – горизонталь (рис. 326, 327).
2. Нормаль к плоскости общего положения – прямая общего положения. Как же определить его направление на чертеже? Можно преобразовать плоскость общего положения в проецирующую и решать как предыдущую задачу. Но вот как решить такую задачу без преобразования чертежа? Предположим, что этот перпендикуляр уже существует. Через его основание на плоскости можно провести пучок прямых. Из этого множества нам выгодно выбрать на плоскости общего положения прямые уровня. Почему? Потому, что мы можем воспользоваться теоремой о проецировании прямого угла в натуральную величину в случае, когда одна из его сторон параллельна плоскости проекций, а другая не перпендикулярна ей.

Поскольку одноимённые прямые уровня плоскости взаимно параллельны, то направление проекций нормали к плоскости общего положения перпендикулярно направлению наклонным проекциям прямых уровня.

При работе с нормалями условимся обозначать их буквой n.

Для определения направления перпендикуляра к плоскости общего положения, заданной треугольником, согласно предыдущему абзацу:

Решим задачу: провести прямую из точки A перпендикулярную к плоскости общего положения, заданной треугольником BDG (рис. 328).

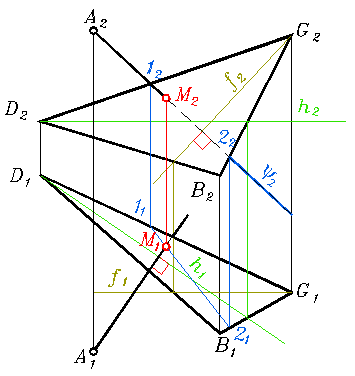
Рис. 328

Руководствуясь приведёнными положениями строим в плоскости прямые уровня. Затем выполняем построения: А_{1 О} n_{1 ^} h₁; А_{2 О} n_{2 ^} f₂.

Чтобы найти основание перпендикуляра, решаем задачу по определению точки пересечения прямой n с плоскостью треугольника BDG: заключаем n во фронтально-проецирующую плоскость Y; тогда Y₂ = n₂; плоскость Y пересекает плоскость треугольника BDG по линии 1-2; пересекается с в точке М; точка М – основание перпендикуляра n, проведённого из точки А к плоскости треугольника BDG.

[Содержание] [Первая] [Назад] [Вперед]