Решение этих задач в конечном счёте сводится к определению расстояния между двумя точками: заданной точкой и ближайшей к ней точкой, принадлежащей геометрическому образу или между двумя ближайшими точками заданных геометрических образов, которые (точки) необходимо определить.
Расстояние между двумя точками измеряется длиной отрезка прямой, соединяющей эти точки. Эти задачи решаются либо способом прямоугольного треугольника (рис. 50, 51), либо преобразованием чертежа для случая, когда построенная прямая занимает общее положение (рис. 224, 225, 226, 236, 239). Если же построенная прямая занимает частное положение, то хотя бы на одну из проекций отрезок спроецируется без искажения (рис. 62, 63; 58, 59, 54, 55, 66, 67, 68, 69, 70, 71).
|
Аудио-комментарии |
Если прямая занимает проецирующее положение, тогда расстоянием от точки до прямой является расстояние между вырожденной в точку проекцией прямой и одноимённой с ней проекцией точки. Причём отрезок, измеряющий расстояние, принадлежит прямой уровня. Так на рис. представлена горизонтально-проецирующая прямая t и точка А. На горизонтальной проекции прямая представлена точкой – t1. Отрезок А1-t1 представляет искомое расстояние между заданной точкой А и горизонтально-проецирующей прямой t. А почему? Давайте докажем.
Итак, на чертеже есть две проекции прямой, одна из них вырождена в точку. Прямая параллельна П2. Согласно теореме о проецировании прямого угла без искажения нормаль, проведённая из фронтальной проекции точки А к прямой t должна быть перпендикулярна к t2. Основанием нормали на прямой t является точка М. Ее горизонтальная проекция совпадает с проекцией прямой t. А теперь рассмотрим проекции отрезка АМ. Как видим это проекции отрезка горизонтали. Наклонная проекция прямых уровня, как известно, обладает метрическими свойствами.
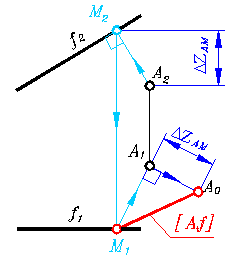
Рис. 335
Из фронтальной проекции А2 проводим нормаль к наклонной проекции фронтали f2. Точка М основание нормали. Находим её горизонтальную проекцию по принадлежности фронтали. А2М2 и А1М1 – проекции нормали, а сам отрезок АМ измеряет расстояние от точки А до заданной фронтали. Но этот отрезок представляет прямую общего положения. Поэтому способом прямоугольного треугольника определяем его натуральную величину.
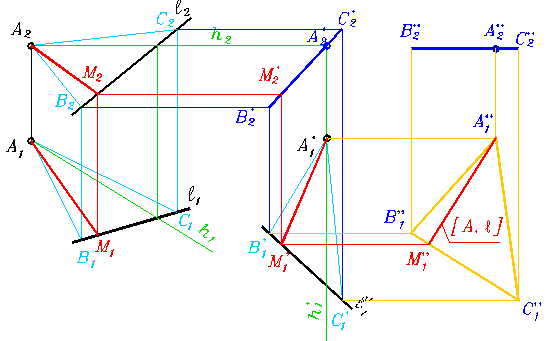
Рис. 336
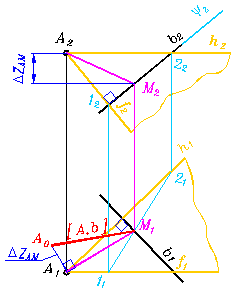
Рис. 337
Без преобразования чертежа: из точки проводим нормаль к заданной прямой. Для этого из точки А проводим фронталь и горизонталь, наклонные проекции которых перпендикулярны проекциям заданной прямой. Тем самым мы сформировали плоскость из точки А, перпендикулярную заданной прямой. Затем с помощью плоскости-посредника Y находим точку пересечения заданной прямой с построенной плоскостью – точку М. Отрезок АМ измеряет расстояние от заданной точки А до заданной прямой b. Однако обе его проекции меньше реального размера. Способом прямоугольного треугольника определяем его натуральную величину.
Эту же задачу можно решать путём преобразования заданной прямой либо в проецирующую прямую уровня, либо в прямую уровня.
Если мы преобразуем прямую в проецирующую, тогда искомое расстояние определится между новой проекцией заданной точки и вырожденной в точку проекцией прямой. Нам понадобятся 2 преобразов
ания. Сначала мы преобразуем заданную прямую в прямую уровня. Вторым преобразованием прямую уровня превратим в проецирующую.
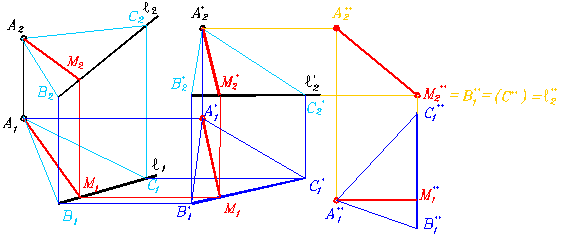
Рис. 338
В то же время можно не проводить второго преобразования. После того, как преобразовали прямую общего положения в прямую уровня мы можем определить направление нормали к заданной прямой и способом прямоугольного треугольника определить натуральную величину её отрезка, измеряющего расстояние. Обоснуйте отсутствие проекции М2 при определении натуральной величины отрезка АМ. Как мы определили направление нормали?
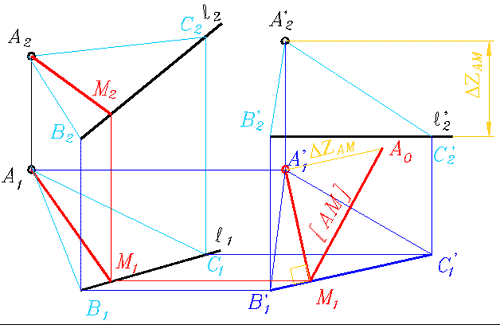
Рис. 339
|
Аудио-комментарии |
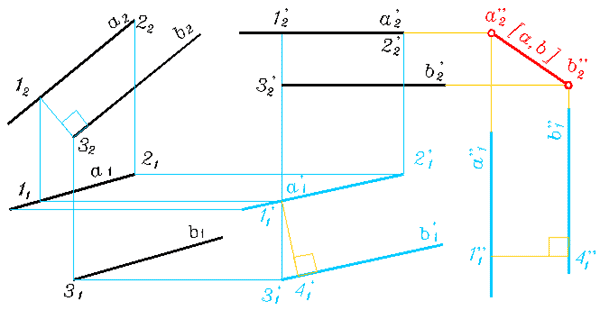
Рис. 340
Преобразуют прямые в проецирующие и тогда искомое расстояние определится между вырожденными в точки проекциями прямых. Сначала мы преобразуем заданные прямые в прямые уровня. Чтобы провести построения перезададим плоскость, которую образуют заданные параллельные прямые, тремя служебными точками - 1, 2, 3. Рекомендуем воспроизвести представленные построения.
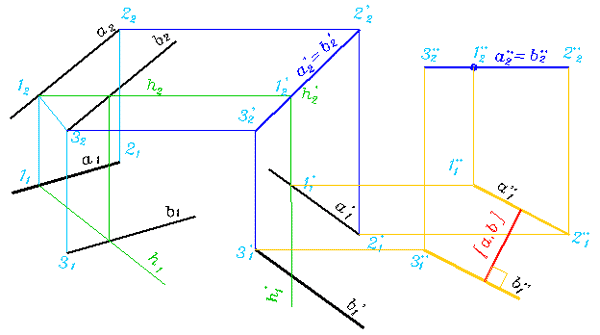
Рис. 341
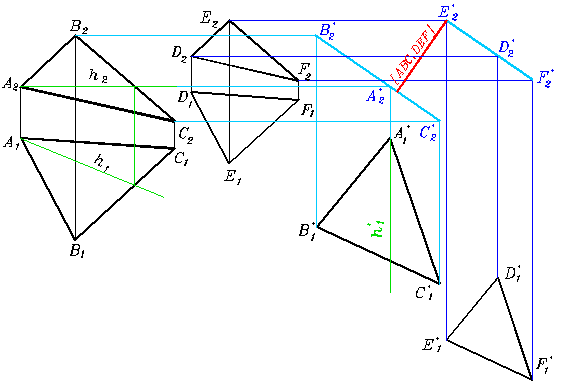
Рис. 342
Расстояние между скрещивающимися прямыми. Прежде всего представим некоторый цилиндр вращения, описанный вокруг одной из заданных прямых, а вторая прямая касается этого цилиндра (рис. 342). Радиус цилиндра и есть искомая величина. Если же мы сумеем ось цилиндра (одну из заданных прямых) и сам цилиндр превратить в проецирующие, то вырожденная в окружность проекция цилиндра – окружность, должна коснуться проекции второй прямой. Чтобы выявить точку касания на вырожденной проекции достаточно из вырожденной в точку проекции прямой провести нормаль к проекции прямой общего положения. Этот отрезок определяет расстояние между заданными скрещивающимися прямыми. На чертеже мы не будем строить проекции цилиндра. Цилиндр нам нужен был только для воображения ближайших точек скрещивающихся прямых.
|
|
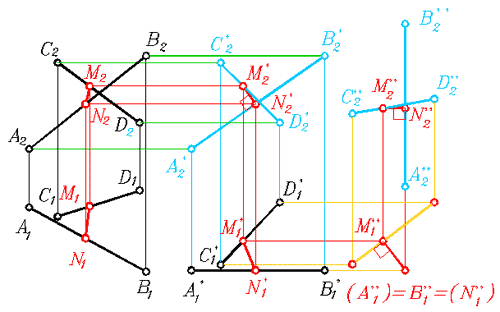 Рис. 343 |
Вид. 32 (Открыть в своём проигрывателе)
На чертеже приведено решение, полученное путём плоскопараллельного перемещения. Отрезок N1''-M1'' - искомое расстояние между скрещивающимися прямыми, а точки М и N - ближайшие точки заданных скрещивающихся прямых. На чертеже построены их проекции на заданном графическом условии. Проследите за построениями.
Попробуйте решить эту задачу без преобразования чертежа. Подсказка: надо заключить заданные прямые во взаимно- параллельные плоскости.
Расстояние от точки до поверхности
вращения
Определим расстояние от точки А до сферы и точку сферы, самую близкую к точке А.
Проанализируем условие. Если бы точка А находилась в одной плоскости с меридианом или экватором, тогда достаточно было бы соединить соответствующую проекцию с центром чтобы определить искомое.
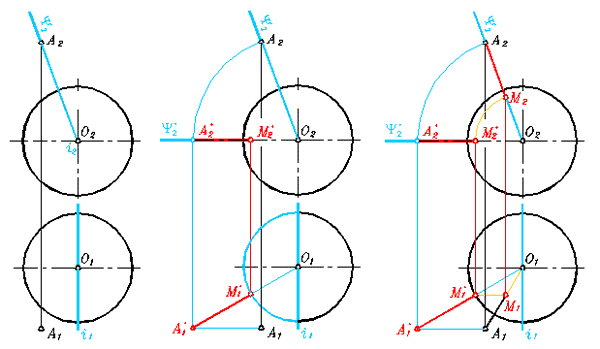
Рис. 344
Давайте решим эту задачу вращением вокруг фронтально-проецирующей прямой – ось i, проходящей через центр сферы. Введём плоскость-посредник – фронтально-проецирующую плоскость Y через заданную точку А и ось i. Эта плоскость-посредник пересекает сферу по полуокружности, которая на плоскость П1 проецируется в полу эллипс. Затем повернём плоскость-посредник вместе с точкой А вокруг оси до горизонта. Теперь сечение плоскостью-посредником спроецируется на П1 без искажения и совпадёт проекцией экватора, и новая проекция точки А лежит в одной плоскости с экватором. Соединим А'1 с О1 и там, где этот отрезок пересечёт экватор обозначим точку М1. Отрезок А'1 - М1 измеряет расстояние от точки А' до преобразованного сечения сферы. То есть этот отрезок определяет расстояние от точки А до сферы, а точка М ближайшая точка сферы к точке А.
Попробуйте решить эту задачу без преобразования чертежа или с преобразованием, но с другой логикой.
Определим расстояние от точки А до торовой поверхности тем же способом.
Вопросы для самопроверки: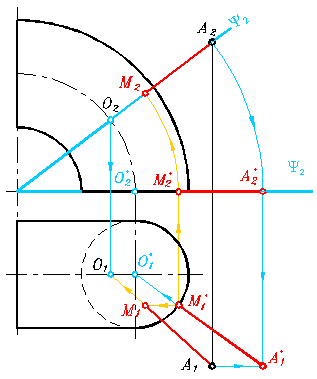
Рис. 345
Вид. 33
(Открыть в своём
проигрывателе)![]()
1. Какое положение в пространстве занимает нормаль к плоскости общего положения? Как найти направление этой нормали, преобразуя чертеж и без преобразования чертежа?
2. В каком случае прямой угол проецируется без искажения?
3. Как определить направление нормали, исходящей из определенной точки к плоскости общего положения, применяя способ преобразования чертежа?
4. Чем следует руководствоваться при решении задач по определению угла между скрещивающимися прямыми?
5. Что является мерой двугранного угла?
6. Как определить расстояние между скрещивающимися прямыми?
7. Что используют при решении задач по определению расстояния от точки до поверхности вращения?