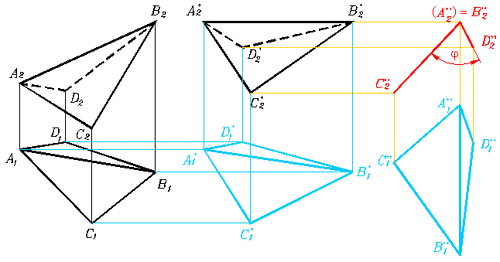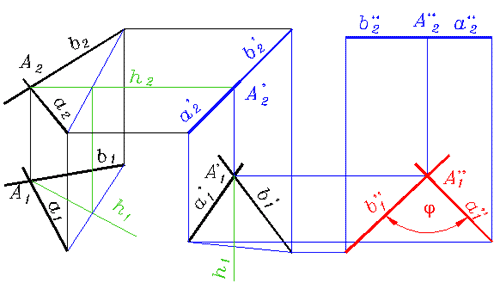
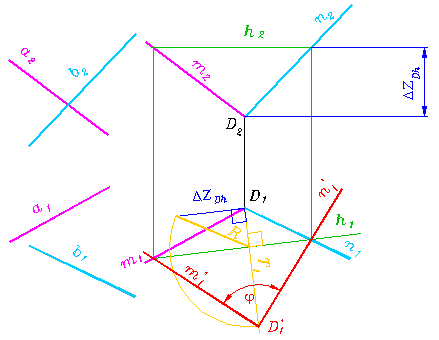
Рис. 331
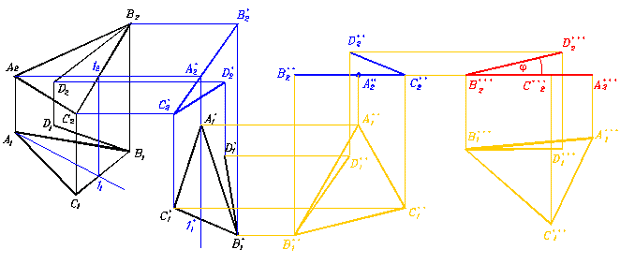
Рис. 332
|
Аудио-комментарии |
нр567
Аудио-комментарии
Придают плоскости проецирующее положение.
- Преобразуют заданную плоскость в плоскость уровня.
- Превращают заданную прямую в прямую уровня.
Способ преобразования чертежа может быть выбран любой.
Решение той же задачи без преобразования чертежа представлено на чертеже (рис. 333) и выглядит очень запутанным.
Давайте проследим за логикой решения без преобразования чертежа.
Прежде всего составим план решения:
- Из точки D опустим перпендикуляр на плоскость треугольника АВС.
- Найдём основание этого перпендикуляра (точку К).
- Соединим точку К с точкой В – тем самым получим проекцию отрезка DB на плоскость треугольника АВС. В результате получим прямоугольный треугольник, у которого угол DBK является искомым. Однако плоскость полученного треугольника будет занимать общее положение, и величина искомого угла будет неопределимой.
- Построим натуральную величину треугольника DBK, что позволит определить величину искомого угла при вершине В.
Решение:
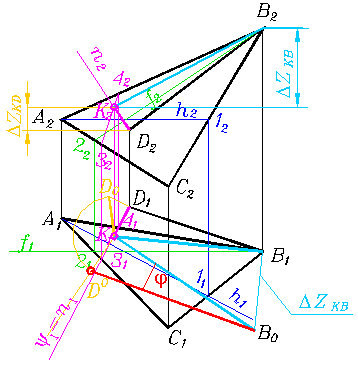
Рис. 333
Очевидно, что логика и графика решения данной задачи без применения способа преобразования чертежа сложны и запутаны.