3. Нормаль к прямой

Нормаль к прямой частного положения – любая прямая, удовлетворяющая теореме о частном случае проецирования прямого угла без искажения.

Например: Пусть через точку А надо провести прямую перпендикулярную к горизонтали. Согласно теореме о частном случае проецирования прямого угла без искажения горизонтальная проекция нормали n₁ ^ h₁, а вот фронтальная h₂ может иметь любое направление

К прямой общего положения можно провести нормаль путём преобразования заданной прямой в прямую уровня и затем применяя теорему о частном случае проецирования прямого угла без искажения, решим подобно алгоритму предидущего абзаца.

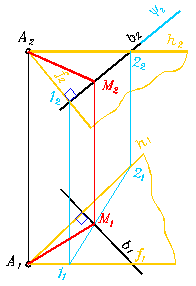
Рис. 329-а

Чтобы построить проекции нормали из точки к прямой общего положения без преобразования чертежа выполняют следующие построения (рис. 329а):

1. Заданную точку A заключают в плоскость, перпендикулярную к заданной прямой. Для этого из заданной точки A проводят горизонталь и фронталь, наклонные проекции которых перпендикулярны одноимённым проекциям заданной прямой b.
2. Находят точку пересечения полученной плоскости (h З f = A) с заданной прямой b. Для этого заключают заданную прямую в проецирующую плоскость-посредник; определяют проекции линии пересечения 1-2 плоскости общего положения, состоящей из горизонтали и фронтали, с плоскостью-посредником; получают точку М пересечения заданной прямой с линией 1-2
3. Соединяют полученную точку М с заданной A. Это и будет отрезок нормали, проведённой из заданной точки A к прямой b.

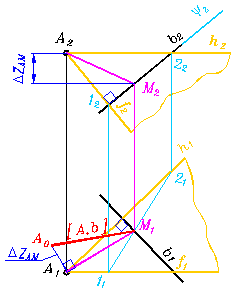
Рис. 329-б

Если требуется определить расстояние от точки до прямой без преобразования чертежа, то четвёртым пунктом определяют величину отрезка АМ способом прямоугольного треугольника (рис 329-б).

[Содержание] [Первая] [Назад] [Вперед]