Простейшая из поверхностей плоскость. В плоскость может выродиться при определенных условиях любая закономерная поверхность. Плоскость - бесконечная во все стороны поверхность, которая на всем своем протяжении не имеет кривизны и преломления. Основной чертеж плоскости может быть представлен отсеком. Отсек может быть ограничен одной или несколькими линиями активного обреза. Это могут быть прямые или кривые линии.
Плоскость - линейчатая поверхность
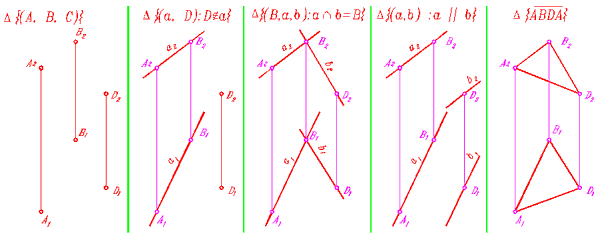
Самый древний определитель плоскости, который можно считать классическим, - три точки, не лежащие на одной прямой (рис. 97).Ту же самую плоскость можно задать прямой и точкой(рис. 98), двумя пересекающими прямыми (рис. 99), двумя параллельными прямыми (рис. 100), треугольным отсеком - треугольником (рис. 101), любой кривой второго порядка и пр.
|
Рис. 97
|
Рис. 98
|
Рис. 99
|
Рис. 100
|
Рис. 101
|
Для закрепления изучаемого материала решите задачи: №18 и №19
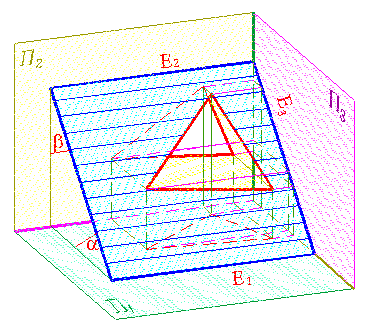
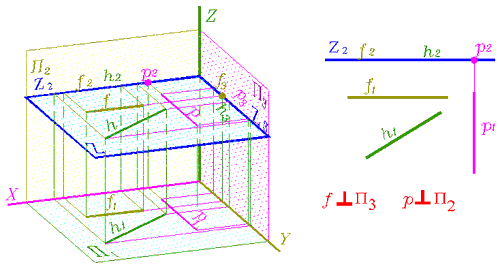
Графический определитель плоскости может быть представлен следами (рис. 103). След плоскости - линия пересечения плоскости с плоскостью проекций. Следами мы будем задавать вырожденные в прямую проекции проецирующих плоскостей и плоскостей уровня.
|
Рис. 102
|
Рис. 103
|
Плоскость можно описать как линейчатую поверхность и задать определителем (рис. 105):
Г (( li, l1, a) : li З a = Ai; li || l1)
Рис. 105
Такое представление соответствует заданию плоскости Г (гамма) двумя параллельными прямыми .
Можно составить определитель плоскости как линейчатой поверхности, который соответствует заданию плоскости точкой и прямой или двумя пересекающимися прямыми (рис. 106):
Г ((l , A, a) : А О li; li З a = Bi ).
Рис. 106
|
Аудио-комментарии |
В зависимости от ориентации плоскости подразделяют на плоскости общего и частного положения.
1. Плоскость общего положения наклонена ко всем плоскостям проекций и составляет с ними непрямые углы (рис. 97-101, 103).
Проекции любой фигуры, которая принадлежит плоскости общего положения, искажены и уменьшены. Только прямые уровня: горизонтали, фронтали и профильные, которые принадлежат плоскости, имеют неискажённые соответствующие их названию проекции.
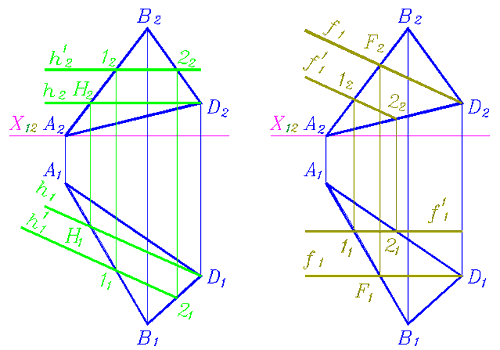
Для решения многих задач следует научиться строить прямые уровня в плоскостях общего положения. Построение начинают с характерной проекции прямой уровня. Ее проводят так, чтобы она прошла через одну из заданных точек плоскости и пересекла некоторую прямую этой же плоскости в точке. Полученную точку называют служебной. Обычно служебные точки обозначают арабскими цифрами.
На рис. 107, 108 построены фронтали и горизонтали плоскости общего положения, заданной треугольником АВD. Они построены через точку D, так как ZA< ZD< ZB и YA< YD< YB. Метрические проекции прямых уровня построены по проекциям точек D, E, H.
|
Рис. 107
|
Рис. 108
|
Для плоскости общего положения характерно то, что её одноименные прямые уровня взаимно параллельны.
Для закрепления изучаемого материала решите задачу №23
2. К плоскостям частного положения относятся проецирующие плоскости и плоскости уровня.
Проецирующие плоскости
Проецирующие плоскости
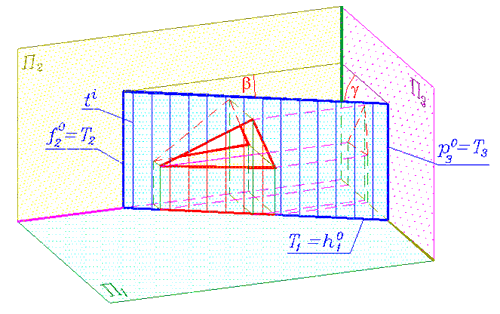
Рис. 109
|
Аудио-комментарии |
Горизонтально-проецирующая плоскость - Т (тау), перпендикулярна к горизонтальной плоскости проекций (рис. 109). Кинематически ее можно представить как непрерывное множество последовательных положений горизонтально-проецирующих прямых, которые пересекают прямолинейную направляющую. Её горизонтали - конкурирующие по отношению к горизонтальной плоскости прямые, а фронтали и профильные прямые являются горизонтально-проецирующими прямыми (рис. 110).
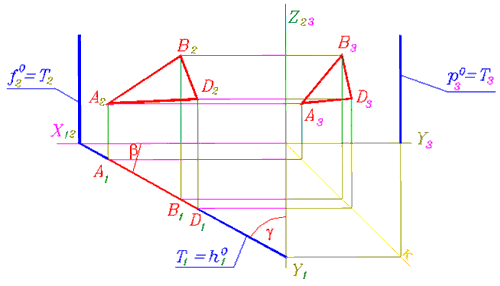
Рис. 110
|
Аудио-комментарии |
|
Рис. 111
|
Рис. 112
|
|
Аудио-комментарии |
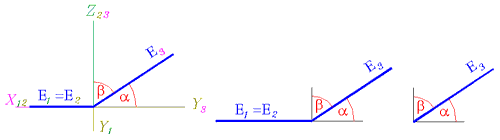
По вырожденной проекции - следу, горизонтально-проецирующей плоскости можно установить углы ее наклона к фронтальной и профильной плоскостям проекций.
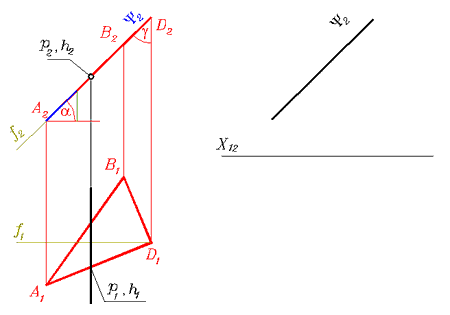
Самостоятельно проведите подобный анализ для фронтально-проецирующей плоскости по рис. 113-116.
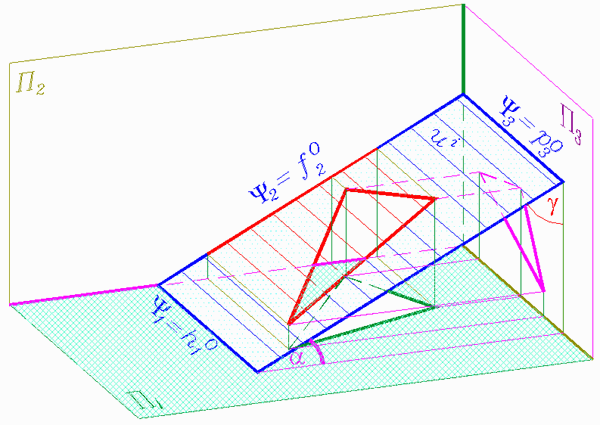
Рис. 113
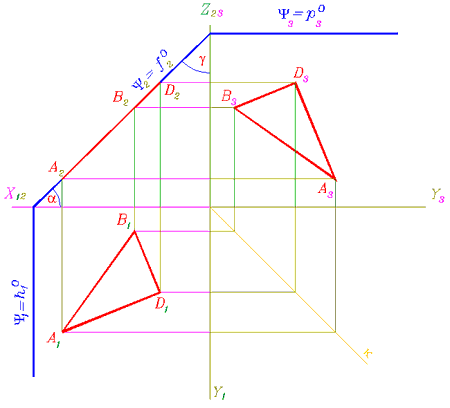
Рис. 114
|
Рис. 115
|
Рис. 116
|
Фронтальная и горизонтальная проекция профильно-проецирующей плоскости похожи на проекции профильно-проецирующей прямой - они параллельны направлению оси 0Х (рис. 117, 119). В целях однозначного прочтения чертежа профильно-проецирующей плоскости, заданной фронтальной и горизонтальной проекциями, необходимо фиксировать положение оси 0Х.
|
Рис. 118
|
Рис. 119
|
Профильно-проецирующая плоскость может пересекать ось 0Х, и тогда ее фронтальная и горизонтальная проекции совпадают. В этом случае либо строят профильную проекцию (рис. 120-122), либо дополняют графический определитель из слившихся следов элементом задаваемой плоскости, например, точкой.
Рис. 120
|
Рис. 121
|
Рис. 122
|
Рис. 123
|
На рис. 123, 124 представлены чертежи профильно-проецирующей плоскости в безосной системе. Если профильно-проецирующая плоскости задана горизонтальной и фронтальной проекциями плоской фигуры, то ее можно опознать по одинаковому направлению фронтали и горизонтали. Фактически это профильно-проецирующие прямые (рис. 125).
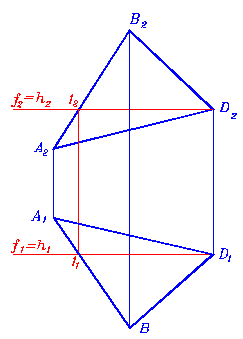
Рис. 125
Плоскости уровня
Плоскость уровня
параллельна одной из плоскостей проекций, которая и определяет название плоскости уровня. Поскольку плоскости проекций взаимно перпендикулярны, то и плоскость уровня перпендикулярна к двум плоскостям проекций. На эти плоскости проекций плоскость уровня проецируется в прямые, которые называют следами.Горизонтальная плоскость параллельна П1 (рис. 126, 127). Её фронтальная и профильная проекции вырожденны в прямую. Эти проекции являются следами. Они перпендикулярны направлению оси 0Х. Для каждой точки горизонтальной плоскости координата z неизменна. След горизонтальной плоскости уровня удобно в дальнейшем обозначать буквой греческого алфавита Z (дзета), что подчеркивает неизменность координаты z для любой её точки.
|
Рис. 126
|
Рис. 127
|
Согласно свойствам ортогонального проецирования всякая плоская фигура, принадлежащая горизонтальной плоскости уровня, на П1 проецируется без искажения (рис. 128). Это положение широко используется при решении метрических и позиционных задач, а также в техническом черчении.
Рис. 128
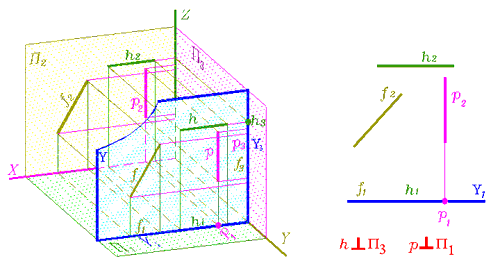
Горизонтали горизонтальной плоскости уровня могут быть различно направленными, а вот фронталь такой плоскости имеет направление профильно-проецирующей прямой. Профильная же прямая горизонтальной плоскости - фронтально-проецирующая прямая (рис. 126, 127).
|
Рис. 129
|
Рис. 130
|
Фронтальная плоскость уровня представлена на рис. 129, 130, профильная - на рис. 131. След фронтальной плоскости уровня удобно в дальнейшем обозначать буквой греческого алфавита Y (ипсилон), что подчеркивает неизменность координаты y для любой её точки.
След профильной плоскости уровня удобно в дальнейшем обозначать буквой греческого алфавита X (хи), что подчеркивает неизменность координаты х для любой её точки.
Самостоятельно проанализируйте положение прямых уровня в этих плоскостях.
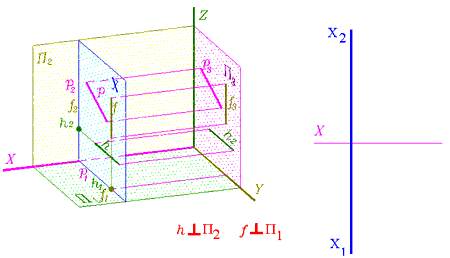
Рис. 131
Различают две задачи о принадлежности точки поверхности:
- Установить принадлежность произвольной точки пространства заданной поверхности.
- По заданной проекции точки и условию ее принадлежности заданной поверхности построить недостающую проекцию точки.
Решение этих задач основано на свойстве ортогонального проецирования: проекция точки, лежащей на поверхности, принадлежит проекции одной из линий этой поверхности (рис. 9). Такую линию мы условились называть носителем.
При решении первой задачи по отношению произвольной точки пространства плоскости общего положения исходим из предположения, что точка принадлежит плоскости. На одной из проекций определяем предполагаемый носитель точки. С помощью служебных точек, в которых носитель пересекает элементы графического определителя плоскости, строим вторую проекцию предполагаемого носителя. Если вторая проекция пройдет через одноименную проекцию точки, то исследуемая точка принадлежит плоскости.
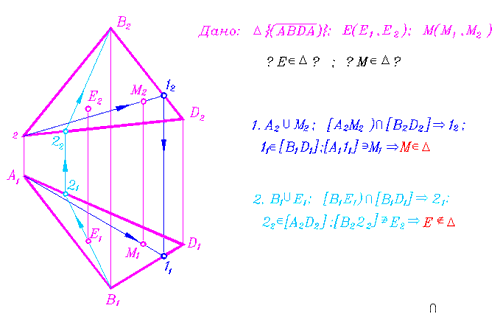
На рис. 132 заданы две точки: Е и М двумя проекциями. Решаем задачу о их принадлежности плоскостям. На фронтальной проекции определяем общий для них предполагаемый носитель. Для этого через их фронтальные проекции проводим прямую до пересечения с элементами задающего плоскость треугольника в точках А2 и 12. Строим горизонтальную проекцию прямой А-1 - A111, по которой видно, что только точка М принадлежит заданной плоскости.
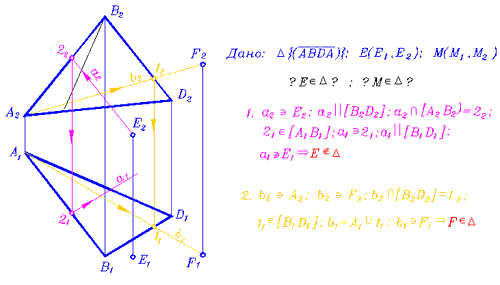
На рис. 133 в качестве предполагаемых носителей точек использованы лучи, параллельные прямым задающим плоскость. Такой приём позволяет строить проекции предполагаемого носителя точки с помощью одной служебной точки.
Точка может принадлежать плоскости даже, если она расположена вне задающих плоскость фигуры или определителя, потому что плоскость бесконечна. Так на рис. 134 проведен анализ принадлежности точек Е и F плоскости заданной треугольником. Проекции этих точек расположены вне треугольных проекций этой плоскости.

Рис. 134
Иллюстрации рис. 132-134 сопровождены алгоритмической записью решения задач.
Алгоритм решения второй задачи о принадлежности точки поверхности состоит в том, что по заданной проекции точки определяют ее носитель на поверхности, строят вторую проекцию носителя и на ней находят недостающую проекцию заданной точки.
Задача о принадлежности точки проецирующей поверхности имеет положительный ответ, если вырожденная проекция поверхности содержит одноименную проекцию точки.
Для закрепления изучаемого материала решите задачи: №20, №21, №22
Вопросы для самопроверки:
1. Чем отличается линия активного обреза поверхности от линии пассивного обреза?
2. Что называется каркасом поверхности?
3. Назовите способы задания плоскости на чертеже.
4. Как можно представить плоскость кинематическим движение прямой по двум напавляющим элементам?
5. Назовите особые линии плоскости.
6. Назовите 7 различных положений плоскости в системе проецирующих плоскостей.
7. В каком случае точка принадлежит плоскости?
8. Как определить принадлежность точки плоскости, если ее проекции не лежат на проекциях этой плоскости?