Прямая может быть наклонена ко всем плоскостям проекций, параллельна одной или двум плоскостям проекций, и во втором случае перпендикулярна третьей плоскости проекций. Прямая может принадлежать одной или двум плоскостям проекций. Ориентация прямой относительно плоскостей проекций зависит от численного соотношения одноименных координат точек, которые составляют определитель прямой.
1. Если все одноименные координаты двух точек различны, то такие точки определяют прямую общего положения. Прямая общего положения наклонена ко всем плоскостям проекций. Проекции прямой общего положения наклонены к осям проекций и к линиям связи.
Проекции отрезка прямой общего положения искажены и меньше его величины.
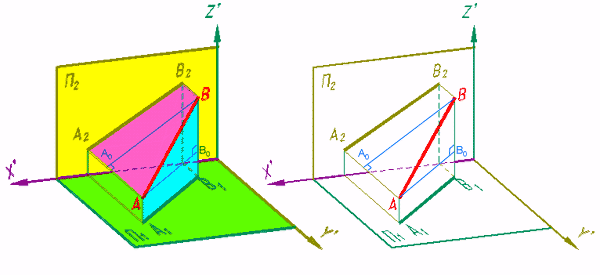
Для решения простейших метрических задач из множества графических способов определения величины отрезка прямой общего положения вначале рассмотрим способ прямоугольного треугольника .
|
Рис. 47 |
При ортогональном проецировании отрезка AB на П2 самим отрезком, проецирующими лучами АА2 и ВВ2, проекцией отрезка А2В2 формируется прямоугольная трапеция АВВ2А2А (рис. 48).
|
|
|
|
|
Рис. 48
|
Рис. 49
|
|
|
||
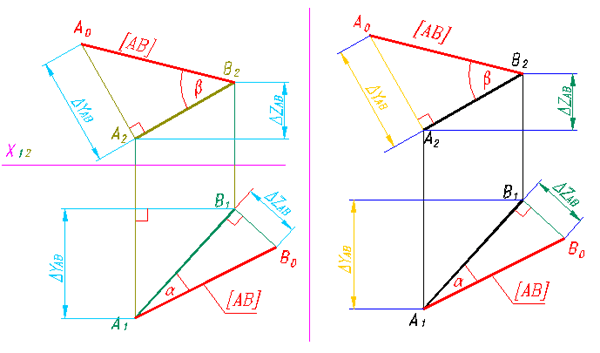
В этой трапеции точка В расположена ближе к П2, чем точка А. Поэтому из точки В проводим прямую, параллельную проекции А2В2, до пересечения с проецирующим лучом АА2. В результате трапеция разделится на две фигуры: прямоугольник - А2В2А0А и прямоугольный треугольник - ВА0А. У прямоугольного треугольника один катет - ВА0, равен проекции В2А2 как противоположная сторона прямоугольника, второй катет - А0А, является разницей ординат - DYAB = YA -YB, гипотенуза - сам отрезок. Воспроизведем на эпюре Монжа треугольник, равный выделенному треугольнику АА0В (рис. 49). В качестве одного катета используем проекцию отрезка - А2В2. Величину второго катета - разницу ординат, определяем графически на горизонтальной проекции. Для этого из В2 проводим прямую, перпендикулярную линиям связи, до пересечения с вертикальной линией связи - А1А2 в точке А0. Отрезок А1А0 является разницей ординат (рис. 50, 51).
Графически разницу координат точек мы научились определять при формировании безосного чертежа (рис. 23). Из любого конца первого катета - А2В2 , строим второй катет. Гипотенуза построенного треугольника является искомой величиной отрезка АВ.
Попутно удалось решить еще одну метрическую задачу: определить величину угла b (бэта) между прямой АВ и П2.
Аналогичные построения можно провести на горизонтальной проекции отрезка АВ - А1В1. Величина второго катета определяется разницей аппликат (рис. 51).
Графически ее можно определить по фронтальной проекции (рис. 23, 50, 51). Попутно определится угол a (альфа) между прямой АВ и П1.
|
Рис. 50
|
Рис. 51
|
На рисунке 51 задача решена в безосной системе. Разницу выстот и ординат определяют по схеме, представленной на рис. 23
Очевидно, что для определения угла g (гамма) наклона прямой к П3 следует построить прямоугольный треугольник на профильной проекции как на катете. Величина второго катета определится разницей абсцисс (рис. 23).
Угол наклона прямой общего положения к плоскости проекций в построенном прямоугольном треугольнике определяется между проекцией отрезка и гипотенузой!
2. Прямые уровня определяются двумя точками, у которых одна из трех координат одинакова. Плоскость, которой параллельна прямая уровня, определяет названия этой прямой.
Прямая, параллельная горизонтальной плоскости, называется горизонталью (рис. 62, 63). Ее обозначают h. Каждая точка такой прямой имеет одинаковую координату Z.
|
|
|
|
|
|
На рис. 64 и 65 представлена нулевая горизонталь - у каждой её точки координата Z = 0, то есть нулевая горизонталь лежит в плоскости П1
|
Рис. 64
|
Рис. 65 |
Фронталь параллельна фронтальной плоскости проекций - П2. Ее обозначают f. Для каждой точки фронтали Y = const (рис. 58, 59).
|
Рис. 58
|
Рис. 59 |
|
Рис. 60
|
Рис. 61 |
Профильная прямая параллельна П3. Для каждой ее точки X = const (рис. 54, 55).
|
Рис. 54
|
Рис. 55 |
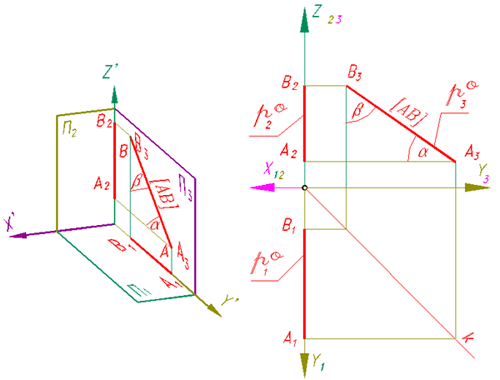
Прямые уровня, которые расположены в самой плоскости проекций, называют нулевыми. На рис. 64, 65 представлена нулевая горизонталь, 60, 61 - нулевая фронталь, 56, 57 - нулевая профильная.
|
Рис. 56
|
Рис. 57 |
Проекции прямых уровня обладают замечательными свойствами. На плоскость, которой прямая уровня параллельна, ее отрезки проецируются без искажения. Неискаженная проекция наклонена и составляет с линиями связи непрямые углы. По наклонной проекции прямой уровня можно установить величины углов наклона прямой к другим плоскостям проекций. Так как наклонная проекция обладает метрическими линейными и угловыми свойствами, условимся называть ее метрической. Проекции прямых уровня, которые перпендикулярны к линиям связи, определяют неизменность одной из координат и параллельность одной из плоскостей проекций, условимся называть характерными.
Для примера рассмотрим проекции горизонтали. У нее метрическая проекция - горизонтальная, а характерные - фронтальная и профильная (рис. 63).
3. Если определитель прямой состоит из двух точек, у которых отличается только одна координата, то эти точки определяют проецирующую прямую. Такая прямая параллельна двум плоскостям проекций и на них проецируется без искажения. Проецирующая прямая параллельна линии пересечения плоскостей, которым она параллельна. А такой линией является ось проекций. У проецирующей прямой проекция, вырожденная в точку, определяет название самой прямой. Для примера рассмотрим горизонтально-проецирующую прямую - рис. 66, 67: горизонтальная проекция вырождена в точку, обладает собирательным свойством, фронтальная и профильная проекции - метрические. Эта прямая параллельна П2, П3 и оси 0Z, и перпендикулярна горизонтальной плоскости проекций.
|
Рис. 66
|
Рис. 67 |
На рис. 68, 69 представлена фронтально-проецирующая прямая, а на рис. 70, 71 - профильно-проецирующая.
|
Рис. 68
|
Рис. 69 |
|
Рис. 70
|
Рис. 71
|
Анализируя относительное положение двух точек в пространстве, мы освоили задание прямой проекциями двух ее точек, которые составляли определитель прямой. Кроме того мы познакомились с различной ориентацией прямой относительно плоскостей уровня, со свойствами проекций прямых частного положения.
Прямую можно также задать графическим определителем, который состоит из двух проекций (рис. 72).
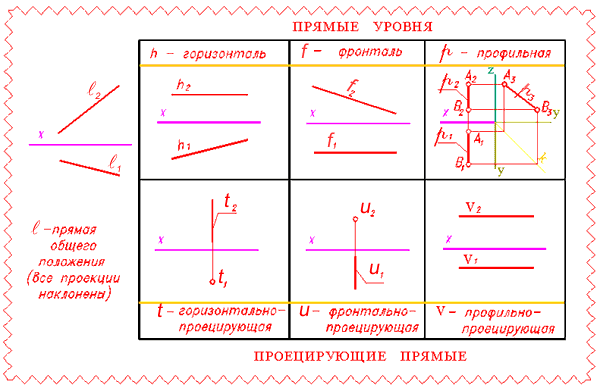
В целях получения обратимого чертежа профильной прямой ее задают либо двумя отрезками на двух картинном чертеже, либо тремя проекциями на комплексном чертеже.
При задании прямой на безосном чертеже следует определить направление вертикальной линии связи заданием любой точки на чертеже (рис. 74, 75).
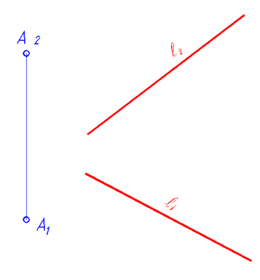 Рис. 74 |
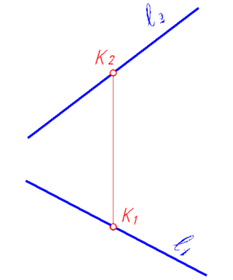 Рис. 75 |
На рис. 72 представлена таблица графических определителей прямых, различно ориентированных относительно плоскостей проекций: l - прямая общего положения; прямые уровня: h - горизонталь, f - фронталь, р - профильная прямая; проецирующие прямые: t - горизонтально-проецирующая, u - фронтально-проецирующая, v - профильно-проецирующая.
Для закрепления изучаемого материала решите задачи: №10, №15, №16
Проецирующую прямую можно задавать только вырожденной в точку проекцией: t1, u2 (рис. 76).
Рис. 73
Невырожденная проекция такой прямой - прямая, лежащая на одной линии связи с вырожденной проекцией. Следует напомнить, что прямую в начертательной геометрии считают одномерным геометрическим образом бесконечной длины.
Точка принадлежит прямой, если её проекции лежат на одноименных проекциях прямой. Например: точка К принадлежит прямой l (рис. 76). Если только одна проекция точки лежит на одноименной проекции прямой, то такая точка расположена либо за прямой -точка А, либо перед прямой - точка В, либо над (выше) -точка D, либо под (ниже) прямой - точка Е. Каждой из указанных точек можно противопоставить конкурирующую с ней точку прямой l . Решение задач о видимости связано с определением видимости точек элемента, проекции которых наложены. Рассмотрим относительное положение точки F и прямой l (рис. 76). Точка F находится над и перед прямой l , ни одна точка прямой l не конкурирует с ней в вопросе видимости.
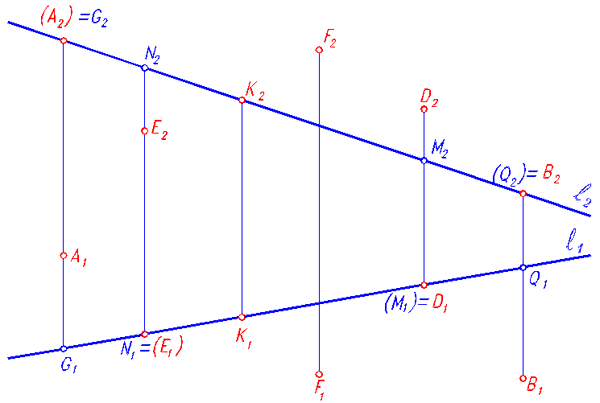
Рис. 76
|
Аудио-комментарии |
Если приходится решать задачу о принадлежности точки профильной прямой, когда проекции точки лежат на одноименных проекциях прямой, то надо построить профильные проекции прямой и точки (рис. 77). Это решение является наиболее точным, графически выразительным и доказательным.
В ряде случаев можно получить отрицательный ответ не строя профильной проекции: согласно свойству ортогонального проецирования о сохранении пропорциональности деления проекции отрезка проекции точки, которая принадлежит отрезку прямой. На рис. 77 видно, что такая пропорциональность деления проекций отрезка АВ проекциями точки D нарушена: D1 делит А1В1 пополам, чего нельзя сказать о фронтальных проекциях отрезка и точки.
Задачи об относительном положении прямой и точки, двух прямых, прямой и поверхности, точки и поверхности, двух поверхностей относятся к позиционным задачам. Прямые - одномерные геометрические образы. Из точек и прямых мы будем формировать более сложные геометрические образы. С помощью прямых мы будем решать более сложные позиционные, а так же и метрические задачи. Поэтому очень важно научится распознавать и строить на чертежах проекции параллельных, пересекающихся и скрещивающихся прямых.
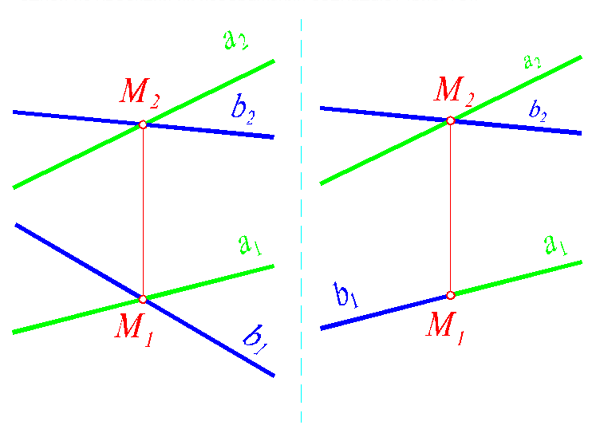
Согласно свойствам ортогонального проецирования одноименные проекции параллельных прямых параллельны (рис. 78). Условие параллельности обозначается символом ||. Параллельные прямые могут занимать по отношению к одной из плоскостей проекций положение конкурирующих прямых. Такие прямые лежат в проецирующей плоскости. На одной из проекций их изображения совпадают (рис. 79).
Также согласно свойствам ортогонального проецирования проекции пересекающихся прямых пересекаются в точках, проекции которых на эпюре Монжа лежат на одной лини связи. Это совершенно естественно: две прямые пересекаются в точке, а проекции точки обязательно располагаются на эпюре Монжа на одной линии связи (рис. 80).
|
Рис. 80
|
Рис. 81 |
На рис. 81 показаны две пересекающиеся прямые, формирующие горизонтально-проецирующюю плоскость. Обратите внимание на видимость прямых на горизонтальной проекции (рис. 81). Условие пересечения записывается символом - З.
Проекции скрещивающихся прямых в обозримом на чертеже пространстве могут пересекаться и не пересекаться. На динамическом рисунке 87 представлены скрещивающиеся прямые.
Вид. 8 (Открыть в своём
проигрывателе)
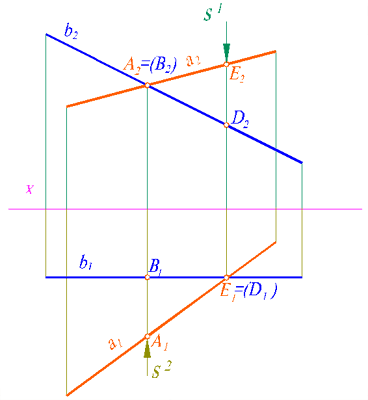
Рис. 88
При движении чётко просматривается отсутствие общей точки. На рисунке 88 мы видим: проекции скрещивающихся прямых пересекаются. Однако, на эпюре Монжа для проекций скрещивающихся прямых характерно то, что точки пересечения проекций не лежат на одной линии связи! Это конкурирующие точки разных прямых (рис. 88). По конкурирующим точкам скрещивающихся линий можно установить видимость элементов при решении позиционных задач и построении чертежа поверхности. То, что линии скрещиваются записываются символом - o .
Для закрепления изучаемого материала решите задачу №17
Точка - нульмерный геометрический образ, может рассматриваться как составной геометрический образ, который можно получить в результате пересечения двух и более геометрических образов. Точку можно получить при пересечении линий (прямых или кривых), линий и поверхностей, трех поверхностей.
Прямая как составной геометрический образ может получаться в результате пересечения двух плоскостей (рис. 82), двух цилиндров (рис. 83), двух конусов (рис. 84) и так далее.
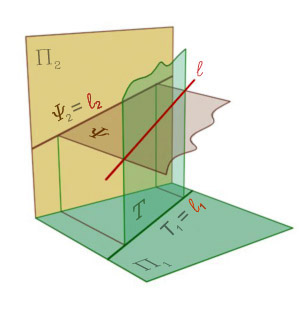
Рис. 82
 Рис. 83 |
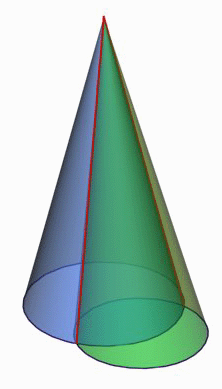 Рис. 84 |
Вид.9 (Открыть в своём проигрывателе) Вид. 10 (Открыть в своём проигрывателе)
В начертательной геометрии кривую линию рассматривают либо как закономерную или случайную траекторию точки, которая движется с изменением направления, либо как составной элемент - линию пересечения двух поверхностей (рис. 85, 86). На рис. 85 показана кривая как результат пересечения плоскости с цилиндрической поверхностью. Безусловно эта кривая плоская. В дальнейшем такие плоские кривые, полученные в результате пересечения поверхности с плоскостью, мы будем называть сечением. На рисунке 86 представлена пространственная кривая полученная в результате пересечения конической и цилиндрической поверхностей.
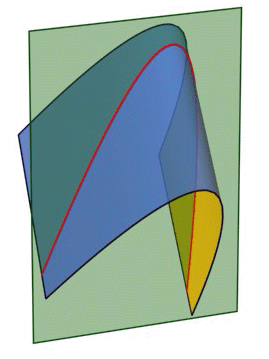 Рис. 85 |
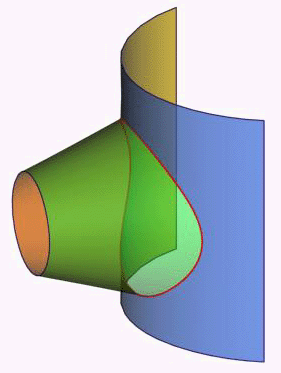 Рис. 86 |
Вид. 11 (Открыть в своём проигрывателе)