Проекции незакономерной кривой строятся по проекциям дискретного (прерывистого) ряда ее точек. Кривая может иметь одну ветвь. Чертеж такой кривой будет вполне обратимым при наличии двух проекций.
Если же у пространственной кривой случайного вида две или более ветвей, то для обратимости чертежа задают проекции одной или более точек на кривой. Число точек зависит от числа ветвей - оно равно числу ветвей минус один. Эти точки устанавливают проекционную связь между проекциями ветвей кривой. На эпюре Монжа точка, которая определяет ветвь, не должна занимать экстремального по координате Х положения.
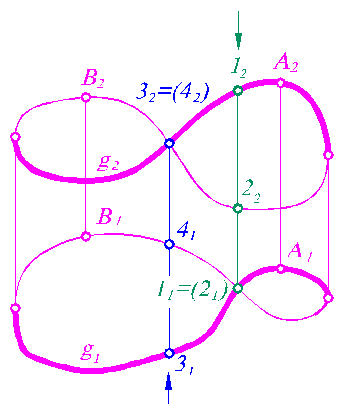
Рис. 89 Вид. 12 (Открыть в своём проигрывателе)
На рис. 89 изображена пространственная кривая. Об этом можно узнать по наличию конкурирующих точек на двух ее проекциях. Изображения пространственных кривых могут и не иметь конкурирующих точек. В таком случае, если требуется , кривую проверяют на плоскостность. Для этого соединяют попарно четыре произвольные точки кривой прямыми. Если прямые пересекаются, то исследуемая кривая плоская (рис. 90), а если скрещиваются - пространственная (рис. 91).
|
Рис. 90
|
Рис. 91 |
Свойства кривых изучаются с помощью касательных и нормалей.
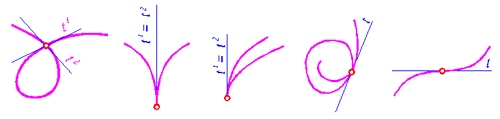
Точки кривой бывают обыкновенными (регулярными) и особыми. Точка кривой называется обыкновенной, если в этой точке можно построить единственную касательную. В противном случае она - особая.
Кривая, которая состоит только из обыкновенных точек, называется монотонной, плавной или гладкой.
|
Рис. 92
|
Рис. 93
|
Рис. 94
|
Рис. 95
|
Рис. 96
|
Особые точки показаны на рис. 92 - узловая, 93 - точка возврата первого рода, 94 - точка возврата второго рода (клюв), 95 - точка самоприкосновения, 96 - точка перегиба. Синим цветом на чертеже изображены касательные.
Касательная к кривой проецируется в касательную к проекциям кривой!
В инженерной практике более всего встречаются кривые второго порядка: окружность, эллипс, парабола, гипербола, а так же трансцендентные кривые: синусоида, циклоиды; коробовые кривые, состоящие из дуг окружностей разных радиусов; конхоидальные кривые - спирали.
При ортогональном проецировании порядок плоской алгебраической кривой не изменяется независимо от наклона их к плоскостям проекций: окружность проецируется в окружность или эллипс, эллипс проецируется в окружность или эллипс, парабола в параболу, гипербола в гиперболу. Исключение составляют вырожденные в прямую проекции этих плоских кривых, если их плоскости являются проецирующими.
Из пространственных кривых более всего применяются гелисы -цилиндрические винтовые линии. Обычно их ориентируют относительно плоскостей проекций так, чтобы ось была перпендикулярна к одной из них. Тогда проекции гелисы - окружность и синусоида.
Применяются так же конические винтовые линии. Они проецируются в спираль Архимеда и в "затухающую" синусоиду.
Вопросы для самопроверки:
1. Что такое прямая общего положения?
2. Каким способом можно определить величину отрезка прямой общего положения и углы наклона ее к плоскостям проекции?
3. Какие прямые называются прямыми уровня?
4. На какой проекции можно установить углы наклона прямой уровня к плоскостям проекции?
5. На какой проекции можно определить натуральную величину отрезка прямой уровня?
6. Что такое нулевая фронталь?
7. У какой прямой уровня фронтальная и горизонтальная проекция перпендикулярна оси ОХ?
8. У какой прямой уровня фронтальная и профильная проекция перпендикулярна оси ОY?
9. Какие прямые называют проецирующими?
10. У какой проецирующей прямой фронтальная и профильная проекции паралельны оси OZ?
11. Каким свойством обладает вырожденная проекция проецирующей прямой?
12. Что обязательно должно присутствовать на безосном чертеже?
13. Какие прямые заданы на рис.73?
14. В каком случае точка принадлежит прямой?
15. В каком случае нельзя установить принадлежность точки прямой по фронтальной и горизонтальной проекции, если проекции точки лежат на проекции этой прямой?
16. В каком случае одноименные проекции прямых паралельны?
17. Чем отличаются проекции пересекающихся прямых от проекций скрещивающихся?
18. Как представить составным геометрическим образом точку?
19. Как определить по чертежу тип кривой линии - плоская она, или пространственная?
20. Что такое обыкновенная точка кривой?
21. Какая точка кривой является особой?
22. Как называется кривая состоящая из обыкновенных точек?
23. У какой кривой одна проекция спираль Архимеда, а другая затухающая синусоида?
24. Что такое гелиса?