Практическая работа №5.
«Использование метода роящихся частиц и генетического алгоритма для нахождения минимума или максимума функции»
Тема 7 «Эвристические алгоритмы»
Цель: получить общее представление об использовании метода роящихся частиц для нахождения экстремумов функции.
Теория:
Метод роящихся частиц
Схема работы алгоритма выглядит следующим образом.
- Создаётся исходная “случайная” популяция частиц.
- Для каждой частицы рассчитывается целевая функция.
- Лучшая частица с точки зрения целевой функции объявляется “центром притяжения”.
- Векторы
скоростей всех частиц устремляются к этому “центру”, при
этом чем дальше частица находится от него, тем большим ускорением она
обладает.
- Осуществляется расчёт новых координат частиц в пространстве решений.
- Шаги 2—5 повторяются заданное число раз.
- Последний “центр тяжести” объявляется найденным оптимальным решением.
Существует несколько разновидностей метода роящихся частиц. Одной из самой простой является стандартный канонический.
Рассмотрим задачу глобальной безусловной минимизации целевой функций 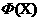 в в 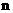 -мерном арифметическом пространстве -мерном арифметическом пространстве 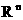 : :
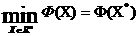 .
(1) .
(1)
Множество частиц обозначим 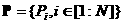 , где , где 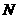 - количество частиц в рое (размер популяции). В момент времени - количество частиц в рое (размер популяции). В момент времени 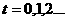 координаты частицы координаты частицы 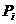 определяются вектором определяются вектором 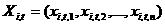 , а ее скорость - вектором , а ее скорость - вектором 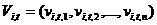 . Начальные координаты и скорости частицы . Начальные координаты и скорости частицы 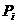 равны равны 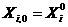 , , 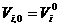 , соответственно. , соответственно.
Итерации в простейшем варианте канонического метода (без
«социальной» составляющей) выполняются по следующей схеме:
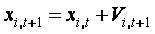 (1) (1)
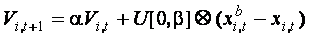 (2), (2),
где t – момент времени (0,1,2, …); хi – вектор
координат i – ой частицы; хb – вектор координат
лучшей частицы, т.е. с наилучшим значением целевой функции Ф(Х); U[0,?]
– вектор псевдослучайных чисел, равномерно распределенных в
интервале [0,?]; ? – свободный параметр, определяет инерционные
свойства частицы; Vi – скорость i-ой частицы.
Свободный параметр 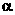 определяет «инерционные» свойства частиц (при определяет «инерционные» свойства частиц (при 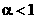 движение частиц, очевидно, замедляется). Рекомендуемое значение параметра движение частиц, очевидно, замедляется). Рекомендуемое значение параметра 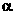 равно 0.7298. В процессе оптимизации может быть эффективным постепенное уменьшение коэффициента равно 0.7298. В процессе оптимизации может быть эффективным постепенное уменьшение коэффициента 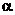 от
0.9 до 0.4. При этом большие значения параметра обеспечивают широкий
обзор пространства поиска, а малые – точную локализацию минимума
целевой функции. Рекомендуемые значения свободного параметра от
0.9 до 0.4. При этом большие значения параметра обеспечивают широкий
обзор пространства поиска, а малые – точную локализацию минимума
целевой функции. Рекомендуемые значения свободного параметра 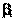 равно 1.49618. равно 1.49618.
Также существует разновидность – модифицированный канонический метод.
В данном методе формула 2 преобразуется к следующему виду:
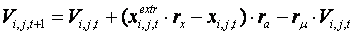 (3) (3)
где
rx обеспечивает неоднозначность положения центра притяжения; rа
обеспечивает неоднозначность величины ускорения; r? обеспечивает
неоднозначность величины коэффициента трения, хextr – центр роя,
т.е. координаты лучшей частицы.
Рекомендуемые значения для r?
– случайное число в интервале от 0.1 до 0.6, а rx и rа случайные
числа в интервале [0, ?].
Генетический алгоритм
Основные понятия, используемые в генетическом алгоритме:
Мутация
— это преобразование хромосомы, случайно изменяющее одну или
несколько ее позиций (генов). Наиболее распространенный вид мутаций
— случайное изменение только одного из генов хромосомы.
Кроссинговер
(в литературе по генетическим алгоритмам также употребляется название
кроссовер или скрещивание) — это операция, при которой из двух
хромосом порождается одна или несколько новых хромосом. В простейшем
случае кроссинговер в генетическом алгоритме реализуется так же, как и
в биологии. При этом хромосомы разрезаются в случайной точке и
обмениваются частями между собой. Например, если хромосомы (1, 2, 3, 4,
5) и (0, 0, 0, 0, 0) разрезать между третьим и четвертым генами и
обменять их части, то получатся потомки (1, 2, 3, 0, 0) и (0, 0, 0, 4,
5).
Работа генетического алгоритма:
Вначале
генерируется начальная популяция особей (индивидуумов), т.е. некоторый
набор решений задачи. Как правило, это делается случайным образом.
Затем моделируется размножение внутри этой популяции. Для этого
случайно отбираются несколько пар индивидуумов, производится
скрещивание между хромосомами в каждой паре, а полученные новые
хромосомы помещаются в популяцию нового поколения. В генетическом
алгоритме сохраняется основной принцип естественного отбора — чем
приспособленнее индивидуум (чем больше соответствующее ему значение
целевой функции), тем с большей вероятностью он будет участвовать в
скрещивании.
Теперь моделируются мутации — в нескольких
случайно выбранных особях нового поколения изменяются некоторые гены.
Затем старая популяция частично или полностью уничтожается и мы
переходим к рассмотрению следующего поколения. Популяция следующего
поколения в большинстве реализаций генетических алгоритмов содержит
столько же особей, сколько начальная, но в силу отбора
приспособленность в ней в среднем выше. Теперь описанные процессы
отбора, скрещивания и мутации повторяются уже для этой популяции и т.
д.
В каждом следующем поколении наблюдается возникновение совершенно новых
решений задачи. Среди них будут как плохие, так и хорошие, но благодаря
отбору число хороших решений будет возрастать. Замечено, что в природе
не бывает абсолютных гарантий, и даже самый приспособленный тигр может
погибнуть от ружейного выстрела, не оставив потомства. Имитируя
эволюцию на компьютере, можно избегать подобных нежелательных событий и
всегда сохранять жизнь лучшему из индивидуумов текущего поколения
— такая методика называется “стратегией элитизма”.
Задание:
- Выполнить
ручной просчет нахождения минимума (максимума) функции методом роящихся
частиц (функция и метод роения выбирается согласно варианту).
Пример: Найти точку минимума функции y(x)=x2 - 2x + 4 (известно что функция достигает минимума при х=2, y(2)=0)
Шаг 1: Построить начальный рой из 5 точек.
В нашем случае, так как функция одной переменной точка будет состоять из одной координаты – это значение Х.
Выберем центр роя (отличный от точки минимума), например х1=-3 и
остальные точки разместим в окрестности центра. Например, х2 = -2,
х3=-1, х4=-4, х5=0.
Найдем значение функции в каждой из пяти точек (таблица 1)
Таблица 1
Номер |
Значение Х |
Значение функции |
Скорость |
1 |
-3 |
25 |
0 |
2 |
-2 |
16 |
0 |
3 |
-1 |
9 |
0 |
4 |
-4 |
36 |
0 |
5 |
0 |
4 |
0 |
Шаг
2: в качестве центра следующего роя выбираем точку с наименьшим
значением функции (так как ищем точку минимума) – это точка х5=0.
Шаг 3:
Пересчитываем координаты остальных точек по формулам (1) и (2), если
реализуется стандартный канонический метод и (1) и (3), если
модифицированный канонический метод.
(В примере в дальнейшем будет рассматриваться стандартный канонический метод)
Случайные составляющие в формуле (2) или (3) для каждой частицы выбираются новые (таблица 2).
Таблица 2
Точка |
Случайные составляющие |
Скорость |
Новое значение координаты |
Х5=0 |
Это лучшая точка (центр создаваемого роя), для нее координаты не пересчитываются |
Х3=-1 |
?=0,7; U = 0,5 |
V = 0,7*0+0,5*(0-(-1))=0.5 |
X3 = -1+0.5=-0.5 |
X2=-2 |
?=0,5; U = 0,8 |
V=0,5*0+0,8*(0-(-2))=1,6 |
X2 = -2+1,6=-0,4 |
X1=-3 |
?=0,6; U = 0,9 |
V=0,6*0+0,9*(0-(-3))=2,7 |
X1 = -3+2,7 = -0,3 |
X4=-4 |
?=0,8; U = 0,7 |
V=0,8*0+0,7*(0-(-4))=2,8 |
X4 = -4+2,8 = -1,2 |
Шаг 4: Находим значения функции в новых точках. Заново заполняем таблицу 1
Таблица 1
Номер |
Значение Х |
Значение функции |
Скорость |
1 |
-0,3 |
5,29 |
0,5 |
2 |
-0,4 |
5,76 |
1,6 |
3 |
-0,5 |
6,25 |
0,5 |
4 |
-1,2 |
10,24 |
2,8 |
5 |
0 |
4 |
0 |
Далее повторяем шаги 2-4 (при ручном просчете повторить еще раз и на этом остановиться)
- Написать
программу, которая реализует алгоритм из ручного просчета (роения
частиц), Повторять шаги (2-4) 50 итераций, т.е. 50 раз будет
создаваться новый рой, выбираться новый центр и т.д. Программа должна
выводить на экран координаты точек роя и значения функции в них после
1, 10, 30, 40, 50 итерации.
- Выполнить
ручной просчет нахождения минимума (максимума) функции генетическим
методом (функция и метод роения выбирается согласно варианту).
Пример:
Найти точку минимума функции y(x)=x2 - 2x + 4 на отрезке хЄ[-10, 10]
(известно что функция достигает минимума при х=2, y(2)=0)
Шаг 1: Возьмем любые пять значений х, принадлежащих отрезку [0, 10]. Например: х1=3, х2 =9 , х3=7, х4=4, х5=0.
Запишем данные значения в двоичной системе.
х1 = 0011; х2
=1001;
х3=0111;
х4=0100; х5=0000
Каждое десятичное значение кодируется двоичным кодом длины 4, так как
граничное значение диапазона 10.
Одно пробное решение, записанное в двоичной форме, называется особью
или хромосомой, а набор всех пробных решений - популяцией
Шаг
2: Принцип естественного отбора заключается в том, что в конкурентной
борьбе выживает наиболее приспособленный. Приспособленность особи
определяется целевой функцией: чем меньше значение целевой функции (так
как мы ищем минимум), тем более приспособленной является
особь.
Определим, какая особь более приспособленная (таблица 1).
Таблица 1
Номер хромосомы (особи) |
Десятичное значение |
Двоичное значение |
Приспособленность |
1 |
3 |
0011 |
1 |
2 |
9 |
1001 |
49 |
3 |
7 |
0111 |
25 |
4 |
4 |
0100 |
4 |
5 |
0 |
0000 |
4 |
Более приспособленной является особь номер 1.
Шаг
3: Процесс размножения - на основе исходной популяции создается новая,
так чтобы пробные решения в новой популяции были ближе к искомому
минимуму целевой функции. Для этого формируются из исходной популяции
брачные пары для скрещивания (кроссинговера).
Пример
операции кроссинговера: скрещиваются две хромосомы 111111 и 000000.
Определяем случайным образом точку разрыва хромосомы, пусть это будет
3. Теперь хромосомы обмениваются частями, стоящими после точки разрыва,
и образуют двух новых потомков: 111000 и 000111.
В нашем случае операция кроссинговера дает следующие результаты:
Таблица 2
Особи родители |
Точка кроссинговера |
Особи потомки |
1 - 0011
2 - 1001 |
1 |
0001
1011 |
3 - 0111
5 - 0000 |
2 |
0100
0011 |
4 - 0100
1 - 0011 |
3 |
0101
0010 |
Шаг
4: мутации – случайные изменения полученных в результате
скрещивания хромосом. Пусть вероятность мутации равна 0,3. Для каждого
потомка берется случайное число на отрезке [0,1], и если это число
меньше 0,3, то инвертируем случайно выбранный ген (заменяем 0 на 1 и
наоборот)
Таблица 3
№ |
Особи потомки |
Случайное
число |
Выбранный ген для мутации |
Потомок после мутации |
Приспособленность потомка |
Десят.
форма |
Дв. форма |
Десят.
форма |
Дв. форма |
до мутации |
после мутации |
1 |
1 |
0001 |
0,3 |
- |
1 |
0001 |
1 |
1 |
2 |
11 |
1011 |
0,1 |
1 |
3 |
0011 |
81 |
1 |
3 |
4 |
0100 |
0,6 |
- |
4 |
0100 |
4 |
4 |
4 |
3 |
0011 |
0,2 |
2 |
7 |
0111 |
1 |
25 |
5 |
5 |
0101 |
0,7 |
- |
5 |
0101 |
9 |
9 |
6 |
2 |
0010 |
0,15 |
3 |
0 |
0000 |
0 |
4 |
Мутации способны улучшить (второй потомок) или ухудшить (4 и 6 потомки) приспособленность особи потомка.
Шаг5:
Из особей родителей (таблица 1) и особей потомков (таблица 3)
необходимо сформировать новую популяцию. В новую популяцию отбираем не
менее 5 наиболее приспособленных особей из числа родителей и потомков.
Строим новую таблицу 1
Таблица 1
Номер хромосомы (особи) |
Десятичное значение |
Двоичное значение |
Приспособленность |
1 |
3 |
0011 |
1 |
2 |
1 |
0001 |
1 |
3 |
4 |
0100 |
4 |
4 |
0 |
0000 |
4 |
5 |
5 |
0101 |
9 |
Далее
снова повторяем шаги 3-5 (для ручного просчета повторить еще раз).
Таким образом, через несколько поколений получается популяция из
похожих и наиболее приспособленных особей. Значение приспособленности
наиболее «хорошей» особи и будет являться минимумом
функции.
- Написать
программу, которая реализует алгоритм из ручного просчета
(генетический), Повторять построение новой популяции 10раз. Программа
должна выводить 1, 3, 5, 7, 10 популяции (все хромосомы популяции и их
приспособленность).
Отчет:
Отчет должен включать следующие разделы:
- Подробное описание ручного просчета для метода роящихся частиц.
- Результаты
работы программы: записать координаты всех 5 точек последнего роя и
значения функции в них. Указать найденный минимум (максимум). Посчитать
погрешность найденного минимума (максимума) от действительного.
- Таблицу двоичного кода (необходимой длины) записи десятичных чисел – для генетического алгоритма.
- Подробное описание ручного просчета генетического алгоритма.
- Результаты
работы программы: записать все хромосомы последней популяции и их
приспособленность. Указать найденный минимум (максимум).
Посчитать погрешность найденного минимума (максимума) от
действительного.
Варианты заданий:
(Вариант совпадает с номером в списке)
Номер
варианта |
Функция |
Диапазон |
1 |
y = 0.5*x2 – 4.8*x + 3.5, найти минимум (y(4,8)=-8,02) |
xЄ[2,15] |
2 |
y=x4-8x2+6, найти минимум (y(2)=-10) |
xЄ[0,10] |
3 |
y=x3-6x2+5, найти минимум (y(4)=-27) |
xЄ[2,15] |
4 |
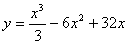 , найти максимум (y(4)=53,3) , найти максимум (y(4)=53,3)
|
xЄ[0,10] |
5 |
y=6x – x2, найти максимум (y(3)=9) |
xЄ[0,10] |
6 |
y=x3-3x2, найти минимум (y(2)=-4) |
xЄ[0,10] |
7 |
y=x4-8x2+7, найти минимум (y(2)=-9) |
xЄ[0,10] |
8 |
y=x4-x3, найти минимум (y(0,75)=0,106) |
xЄ[0,10] |
9 |
y=5+4x-x2, найти максимум (y(2)=9) |
xЄ[0,10] |
10 |
y=3x4-4x3, найти минимум (y(1)=-1) |
xЄ[0,10] |
11 |
y=3(x-1)2+1, найти минимум (y(1)=1) |
xЄ[0,10] |
12 |
y=2x2-x4, найти максимум (y(1)=1) |
xЄ[0,10] |
|