Тема 7. Нечеткая логика
Для представления нечетких понятий и оперирования с ними американский ученый Л.Заде в 60-х годах разработал теорию нечетких множеств, а затем – нечеткую логику, базирующуюся на ней. В основе теории нечетких множеств лежит интерпретация факта принадлежности элемента a множеству A как факта, который может быть истинным или ложным с некоторой оценкой истинности ?A(a), пробегающей значения от 0 до 1. Эта оценка истинности называется функцией принадлежности элемента a множеству A. Операции включения и равенства в теории нечетких множеств определяются обычно следующим образом (по Л.Заде):
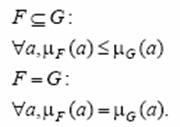
Дополнение множества F к G определяется так, что
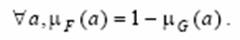
Пересечение и объединение множеств определяются следующим образом:
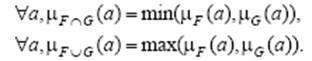
Эти определения не единственные, хотя они не противоречат интуитивным представлениям о соответствующих операциях над нечеткими множествами.
Частным случаем теории нечетких множеств (при ? = 1 или 0) является классическая теория множеств. Однако встречаются и другие определения операций над нечеткими множествами.
Так же как на основе классической теории множеств строится двоичная (булева) логика, так и на базе теории нечетких множеств строится теория нечетких множеств. Она оперирует с высказываниями, для которых функция принадлежности, описанная ранее, определена на множестве истинных высказываний. Функция принадлежности интерпретируется как мера истинности, уверенности или достоверности и отражает нечеткость знаний.
Предположим, существуют следующие высказывания:
"Иванов – хороший человек" с ? =0.8,
"Политик – хороший человек" с ? = 0.3.
Тогда конъюнкция этих двух высказываний (имеющая смысл как уточнение мнения об Иванове, когда стало известно, что он – политик) определяется функцией принадлежности ? = 0.3, а дизъюнкция – ? = 0.8.
Понятие нечеткого множества введено как обобщение понятия характеристической функции множества. Нечеткое подмножество A универсального множества X задается функцией принадлежности ?A:X>L, где L = [0,1]. Для каждого xЄX величина ?A(x) интерпретируется как степень принадлежности элемента x нечеткому множеству A.
В теории нечетких множеств функция принадлежности может интерпретироваться как субъективное представление об истинности высказываний или объективная нечеткость знаний (информации). В первом случае описание нечетких высказываний является как бы снимком состояния некоторой интеллектуальной системы, обученной на примерах взаимодействия с внешней средой или заполненной субъективными знаниями экспертов. Во втором случае нечеткость является следствием каких-либо помех при поступлении информации в систему и интерпретации ее в виде знаний. В обоих случаях функцию принадлежности можно интерпретировать как вероятностную меру истинности и применять теорию вероятности к ее обработке и анализу. Это справедливо, т.к. интеллектуальная система работает с множеством разных субъектов, имеющих разные субъективные представления об истинности высказываний, или с множеством разных ситуаций, в которых разные помехи создают вероятностное описание истинности информации (знаний).
Недостатки классической логики и основанной на ней логики предикатов первого порядка как метода представления знаний об окружающем мире привели к появлению псевдофизических логик. В их основе лежит представление нечетких или размытых понятий в виде так называемых лингвистических переменных, придуманных Заде для того, чтобы приблизить семантику (смысл) денотата (знака) к семантике, которая вырабатывается в мозгу человека в процессе его обучения (опыта). Для этого множество образов (десигнатов), с которыми должна оперировать интеллектуальная система, представляется в виде точек на шкалах.
Лингвистической переменной называют переменную, значениями которой являются слова или предложения естественного или искусственного языка.
Например, можно рассматривать лингвистические переменные "возраст" (в годах), "расстояние до объекта" (в м или км) и т.п. Значение линг. переменной "возраст" могут быть значения: "юный", "молодой", "зрелый", "пожилой", "старый", "дряхлый". С переменной "расстояние" – "вплотную", "очень близко", "близко", "рядом", "недалеко", "далеко", "очень далеко", "у черта на куличиках". Взаимосвязь между этими двумя представлениями (множеством точек на шкале и множеством знаковых значений) задается с помощью функции принадлежности ?x(t) , где x – значение лингвистической переменной, t – значение на шкале.
Значение функции принадлежности интерпретируется как вероятность того, что значение t на шкале можно заменить знаком x или наоборот. Очевидно, что можно пронормировать значения функции принадлежности в соответствии с формулой:
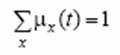
или в соответствии с
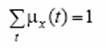
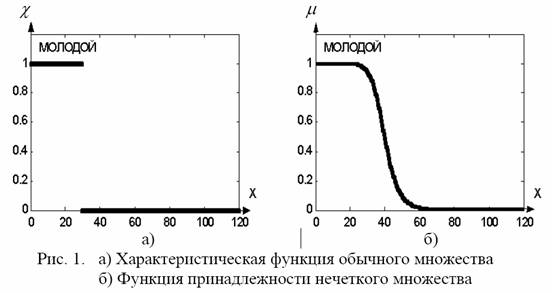
На рис. 2 приведен пример описания лингвистической переменной возраст. Здесь каждая кривая описывает ее одно символьное значение. Наиболее используемыми псевдофизическими логиками являются пространственная, временная и каузальная (причинно-следственная).
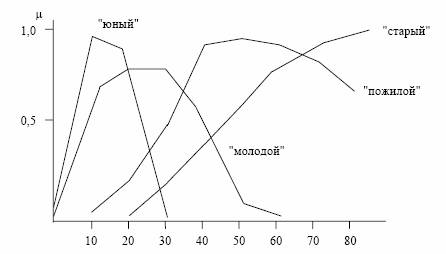
Рис. 2 Описание лингвистической переменной «Возраст»
В качестве операций конъюнкции, дизъюнкции и отрицания на [0,1] Заде предложил следующее обобщение булевых функций:
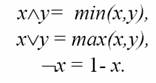
Значения, которые может принимать лингвистическая переменная, называется термами. Термы лингвистических переменных являются нечеткими переменными. Терм, состоящий из одного слова, называется атомарным термом. Производные от атомарных термов, получаемые путем уточнения «очень», «не очень», «более или менее», называются подтермами.
Нечеткая логика работает даже тогда, когда хороших решений нет, тем не менее решение, пусть даже плохое, принять надо. Поскольку значение лингвистической переменной «размазано» по числовой прямой, даже при наложении друг на друга взаимоисключающих ограничений решение получается за счет «хвостов» функции совместимости.
Пример
Лингвистическая переменная задается пятеркой 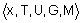 , где , где 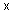 - имя переменной; - имя переменной; 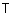 - терм-множество, каждый элемент которого (терм) представляется как нечеткое множество на универсальном множестве - терм-множество, каждый элемент которого (терм) представляется как нечеткое множество на универсальном множестве 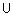 ; ; 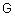 - синтаксические правила, часто в виде грамматики, порождающие название термов; - синтаксические правила, часто в виде грамматики, порождающие название термов; 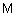 - семантические правила, задающие функции принадлежности нечетких термов, порожденных синтаксическими правилами - семантические правила, задающие функции принадлежности нечетких термов, порожденных синтаксическими правилами 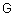 . .
Рассмотрим лингвистическую переменную с именем 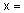 "температура в комнате". Тогда оставшуюся четверку "температура в комнате". Тогда оставшуюся четверку 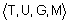 можно определить так: можно определить так:
- универсальное множество -
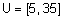 ; ;
- терм-множество -
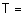 {"холодно", "комфортно", "жарко"} с такими функциями принадлежностями ( {"холодно", "комфортно", "жарко"} с такими функциями принадлежностями (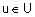 ): ):
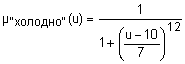 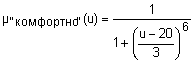 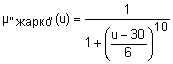 - синтаксические правила
 , порождающее новые термы с использованием квантификаторов "не", "очень" и "более-менее"; , порождающее новые термы с использованием квантификаторов "не", "очень" и "более-менее";
- семантические правила
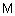 , в виде таблицы 1. , в виде таблицы 1.
Таблица 1 - Правила расчета функций принадлежности
Квантификатор |
Функция принадлежности (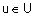 ) ) |
не t |
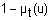
|
очень t |
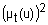
|
более-менее t |
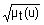
|
Графики функций принадлежности термов "холодно", "не очень холодно", "комфортно", "более-менее комфортно", "жарко" и "очень жарко" лингвистической переменной "температура в комнате" показаны на рис. 1.
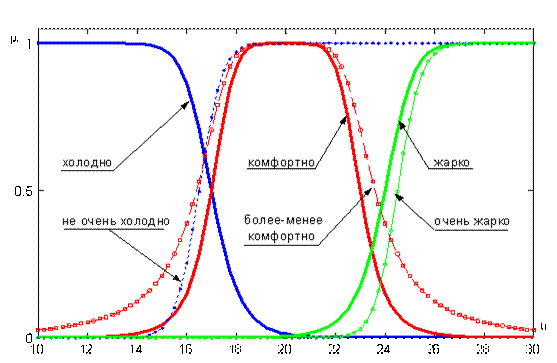
Рисунок 1- Лингвистическая переменная "температура в комнате"
|