Тема 4. Системы распознавания образов
Образ,
класс — классификационная группировка в системе классификации,
объединяющая (выделяющая) определенную группу объектов по некоторому
признаку.
Образное восприятие мира — одно из загадочных
свойств живого мозга, позволяющее разобраться в бесконечном потоке
воспринимаемой информации и сохранять ориентацию в океане разрозненных
данных о внешнем мире. Воспринимая внешний мир, мы всегда производим
классификацию воспринимаемых ощущений, т. е. разбиваем их на группы
похожих, но не тождественных явлений. Например, несмотря на
существенное различие, к одной группе относятся все буквы А, написанные
различными почерками, или все звуки, соответствующие одной и той же
ноте, взятой в любой октаве и на любом инструменте, а оператор,
управляющий техническим объектом, на целое множество состояний объекта
реагирует одной и той же реакцией. Характерно, что для составления
понятия о группе восприятий определенного класса достаточно
ознакомиться с незначительным количеством ее представителей. Ребенку
можно показать всего один раз какую-либо букву, чтобы он смог найти эту
букву в тексте, написанном различными шрифтами, или узнать ее, даже
если она написана в умышленно искаженном виде. Это свойство мозга
позволяет сформулировать такое понятие, как образ.
Образы обладают характерным свойством, проявляющимся в том, что
ознакомление с конечным числом явлений из одного и того же множества
дает возможность узнавать сколь угодно большое число его
представителей. Примерами образов могут быть: река, море, жидкость,
музыка Чайковского, стихи Маяковского и т. д. В качестве образа можно
рассматривать и некоторую совокупность состояний объекта управления,
причем вся эта совокупность состояний характеризуется тем, что для
достижения заданной цели требуется одинаковое воздействие на объект.
Образы обладают характерными объективными свойствами в том смысле, что
разные люди, обучающиеся на различном материале наблюдений, большей
частью одинаково и независимо друг от друга классифицируют одни и те же
объекты. Именно эта объективность образов позволяет людям всего мира
понимать друг друга.
Способность восприятия внешнего мира в форме образов позволяет с
определенной достоверностью узнавать бесконечное число объектов на
основании ознакомления с конечным их числом, а объективный характер
основного свойства образов позволяет моделировать процесс их
распознавания. Будучи отражением объективной реальности, понятие образа
столь же объективно, как и сама реальность, а поэтому это понятие может
быть само по себе объектом специального исследования.
В литературе, посвященной проблеме обучения распознавания образов
(ОРО), часто вместо понятия образа вводится понятие класса.
Одним
из самых интересных свойств человеческого мозга является способность
отвечать на бесконечное множество состояний внешней среды конечным
числом реакций. Может быть, именно это свойство позволило человеку
достигнуть высшей формы существования живой материи, выражающейся в
способности к мышлению, т. е. активному отражению объективного мира в
виде образов, понятий, суждений и т. д. Поэтому проблема ОРО возникла
при изучении физиологических свойств мозга.
В
целом проблема распознавания образов состоит из двух частей: обучения и
распознавания. Обучение осуществляется путем показа отдельных объектов
с указанием их принадлежности тому или другому образу. В результате
обучения распознающая система должна приобрести способность реагировать
одинаковыми реакциями на все объекты одного образа и различными —
на все объекты различных образов. Очень важно, что процесс обучения
должен завершиться только путем показов конечного числа объектов без
каких-либо других подсказок. В качестве объектов обучения могут быть
либо картинки, либо другие визуальные изображения (буквы), либо
различные явления внешнего мира, например звуки, состояния организма
при медицинском диагнозе, состояние технического объекта в системах
управления и др. Важно, что в процессе обучения указываются только сами
объекты и их принадлежность образу. За обучением следует процесс
распознавания новых объектов, который характеризует действия уже
обученной системы. Автоматизация этих процедур и составляет проблему
обучения распознаванию образов. В том случае, когда человек сам
разгадывает или придумывает, а затем навязывает машине правило
классификации, проблема распознавания решается частично, так как
основную и главную часть проблемы (обучение) человек берет на себя.
Проблема обучения распознаванию образов интересна как с прикладной, так
и с принципиальной точки зрения. С прикладной точки зрения решение этой
проблемы важно прежде всего потому, что оно открывает возможность
автоматизировать многие процессы, которые до сих пор связывали лишь с
деятельностью живого мозга. Принципиальное значение проблемы тесно
связано с вопросом, который все чаще возникает в связи с развитием идей
кибернетики: что может и что принципиально не может делать машина? В
какой мере возможности машины могут быть приближены к возможностям
живого мозга? В частности, может ли машина развить в себе способность
перенять у человека умение производить определенные действия в
зависимости от ситуаций, возникающих в окружающей среде? Пока стало
ясно только то, что если человек может сначала сам осознать свое
умение, а потом его описать, т. е. указать, почему он производит
действия в ответ на каждое состояние внешней среды или как (по какому
правилу) он объединяет отдельные объекты в образы, то такое умение без
принципиальных трудностей может быть передано машине. Если же человек
обладает умением, но не может объяснить его, то остается только один
путь передачи умения машине — обучение примерами.
Круг задач, которые могут решаться с помощью распознающих систем,
чрезвычайно широк. Сюда относятся не только задачи распознавания
зрительных и слуховых образов, но и задачи распознавания сложных
процессов и явлений, возникающих, например, при выборе целесообразных
действий руководителем предприятия или выборе оптимального управления
технологическими, экономическими, транспортными или военными
операциями. В каждой из таких задач анализируются некоторые явления,
процессы, состояния внешнего мира, всюду далее называемые объектами
наблюдения. Прежде чем начать анализ какого-либо объекта, нужно
получить о нем определенную, каким-либо способом упорядоченную
информацию. Такая информация представляет собой характеристику
объектов, их отображение на множестве воспринимающих органов
распознающей системы.
Но каждый объект наблюдения может воздействовать по-разному, в
зависимости от условий восприятия. Например, какая-либо буква, даже
одинаково написанная, может в принципе как угодно смещаться
относительно воспринимающих органов. Кроме того, объекты одного и того
же образа могут достаточно сильно отличаться друг от друга и,
естественно, по-разному воздействовать на воспринимающие органы.
Каждое отображение какого-либо объекта на воспринимающие органы
распознающей системы, независимо от его положения относительно этих
органов, принято называть изображением объекта, а множества таких
изображений, объединенные какими-либо общими свойствами, представляют
собой образы.
При решении задач управления методами распознавания образов вместо
термина "изображение" применяют термин "состояние". Состояние —
это определенной формы отображение измеряемых текущих (или мгновенных)
характеристик наблюдаемого объекта. Совокупность состояний определяет
ситуацию. Понятие "ситуация" является аналогом понятия "образ". Но эта
аналогия не полная, так как не всякий образ можно назвать ситуацией,
хотя всякую ситуацию можно назвать образом.
Ситуацией принято называть некоторую совокупность состояний сложного
объекта, каждая из которых характеризуется одними и теми же или схожими
характеристиками объекта. Например, если в качестве объекта наблюдения
рассматривается некоторый объект управления, то ситуация объединяет
такие состояния этого объекта, в которых следует применять одни и те же
управляющие воздействия. Если объектом наблюдения является военная
игра, то ситуация объединяет все состояния игры, которые требуют,
например, мощного танкового удара при поддержке авиации.
Выбор исходного описания объектов является одной из центральных задач
проблемы ОРО. При удачном выборе исходного описания (пространства
признаков) задача распознавания может оказаться тривиальной и,
наоборот, неудачно выбранное исходное описание может привести либо к
очень сложной дальнейшей переработку информации, либо вообще к
отсутствию решения. Например, если решается задача распознавания
объектов, отличающихся по цвету, а в качестве исходного описания
выбраны сигналы, получаемые от датчиков веса, то задача распознавания в
принципе не может быть решена.
Каждый
раз, когда сталкиваются с незнакомыми задачами, появляется естественное
желание представить их в виде некоторой легко понимаемой модели,
которая позволяла бы осмыслить задачу в таких терминах, которые легко
воспроизводятся нашим воображением. А так как мы существуем в
пространстве и во времени, наиболее понятной для нас является
пространственно-временная интерпретация задач.
Любое изображение,
которое возникает в результате наблюдения какого-либо объекта в
процессе обучения или экзамена, можно представить в виде вектора, а
значит и в виде точки некоторого пространства признаков. Если
утверждается, что при показе изображений возможно однозначно отнести их
к одному из двух (или нескольких) образов, то тем самым утверждается,
что в некотором пространстве существует две (или несколько) области, не
имеющие общих точек, и что изображения — точки из этих областей.
Каждой такой области можно приписать наименование, т. е. дать название,
соответствующее образу.
Проинтерпретируем теперь в терминах геометрической картины процесс
обучения распознаванию образов, ограничившись пока случаем
распознавания только двух образов. Заранее считается известным лишь
только то, что требуется разделить две области в некотором пространстве
и что показываются точки только из этих областей. Сами эти области
заранее не определены, т. е. нет каких-либо сведений о расположении их
границ или правил определения принадлежности точки к той или иной
области.
В ходе обучения предъявляются точки, случайно выбранные из этих
областей, и сообщается информация о том, к какой области принадлежат
предъявляемые точки. Никакой дополнительной информации об этих
областях, т. е. о расположении их границ, в ходе обучения не
сообщается. Цель обучения состоит либо в построении поверхности,
которая разделяла бы не только показанные в процессе обучения точки, но
и все остальные точки, принадлежащие этим областям, либо в построении
поверхностей, ограничивающих эти области так, чтобы в каждой из них
находились только точки одного образа. Иначе говоря, цель обучения
состоит в построении таких функций от векторов-изображений, которые
была бы, например, положительны на всех точках одного и отрицательны на
всех точках другого образа. В связи с тем, что области не имеют общих
точек, всегда существует целое множество таких разделяющих функций, а в
результате обучения должна быть построена одна из них.
Если предъявляемые изображения принадлежат не двум, а большему числу
образов, то задача состоит в построении по показанным в ходе обучения
точкам поверхности, разделяющей все области, соответствующие этим
образам, друг от друга. Задача эта может быть решена, например, путем
построения функции, принимающей над точками каждой из областей
одинаковое значение, а над точками из разных областей значение этой
функции должно быть различно.
Рис. 1. Два образа.
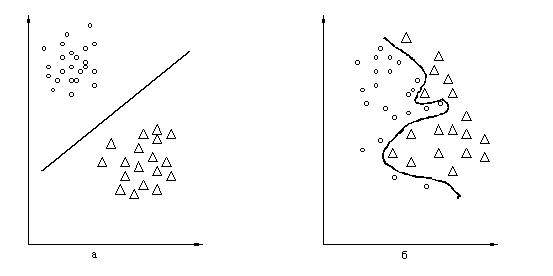
На первый взгляд кажется, что знание всего лишь некоторого количества
точек из области недостаточно, чтобы отделить всю область.
Действительно, можно указать бесчисленное количество различных
областей, которые содержат эти точки, и как бы ни была построена по ним
поверхность, выделяющая область, всегда можно указать другую область,
которая пересекает поверхность и вместе с тем содержит показанные
точки. Однако известно, что задача о приближении функции по информации
о ней в ограниченном множестве точек, существенно более узкой, чем все
множество, на котором функция задана, является обычной математической
задачей об аппроксимации функций. Разумеется, решение таких задач
требует введения определенных ограничений на классе рассматриваемых
функций, а выбор этих ограничений зависит от характера информации,
которую может добавить учитель в процессе обучения. Одной из таких
подсказок является гипотеза о компактности образов. Интуитивно ясно,
что аппроксимация разделяющей функции будет задачей тем более легкой,
чем более компактны и чем более разнесены в пространстве области,
подлежащие разделению. Так, например, в случае, показанном на
Рис. 1а, разделение заведомо более просто, чем в случае,
показанном на Рис. 1б. Действительно, в случае, изображенном на
Рис. 1а, области могут быть разделены плоскостью, и даже при
больших погрешностях в определении разделяющей функции она все же будет
продолжать разделять области. В случае же на Рис. 1б, разделение
осуществляется замысловатой поверхностью и даже незначительные
отклонения в ее форме приводят к ошибкам разделения. Именно это
интуитивное представление о сравнительно легко разделимых областях
привело к гипотезе компактности.
Наряду с геометрической интерпретацией проблемы обучения распознаванию
образов существует и иной подход, который назван структурным, или
лингвистическим. Поясним лингвистический подход на примере
распознавания зрительных изображений. Сначала выделяется набор исходных
понятий — типичных фрагментов, встречающихся на изображениях, и
характеристик взаимного расположения фрагментов — "слева",
"снизу", "внутри" и т. д. Эти исходные понятия образуют словарь,
позволяющий строить различные логические высказывания, иногда
называемые предположениями. Задача состоит в том, чтобы из большого
количества высказываний, которые могли бы быть построены с
использованием этих понятий, отобрать наиболее существенные для данного
конкретного случая.
Далее, просматривая конечное и по возможности небольшое число объектов
из каждого образа, нужно построить описание этих образов. Построенные
описания должны быть столь полными, чтобы решить вопрос о том, к какому
образу принадлежит данный объект. При реализации лингвистического
подхода возникают две задачи: задача построения исходного словаря, т.
е. набор типичных фрагментов, и задача построения правил описания из
элементов заданного словаря.
В рамках лингвистической интерпретации проводится аналогия между
структурой изображений и синтаксисом языка. Стремление к этой аналогии
было вызвано возможностью использовать аппарат математической
лингвистики, т. е. методы по своей природе являются синтаксическими.
Использование аппарата математической лингвистики для описания
структуры изображений можно применять только после того, как
произведена сегментация изображений на составные части, т. е.
выработаны слова для описания типичных фрагментов и методы их поиска.
После предварительной работы, обеспечивающей выделение слов, возникают
собственно лингвистические задачи, состоящие из задач автоматического
грамматического разбора описаний для распознавания изображений. При
этом проявляется самостоятельная область исследований, которая требует
не только знания основ математической лингвистики, но и овладения
приемами, которые разработаны специально для лингвистической обработки
изображений.
СИСТЕМАТИКА МЕТОДОВ РАСПОЗНАВАНИЯ
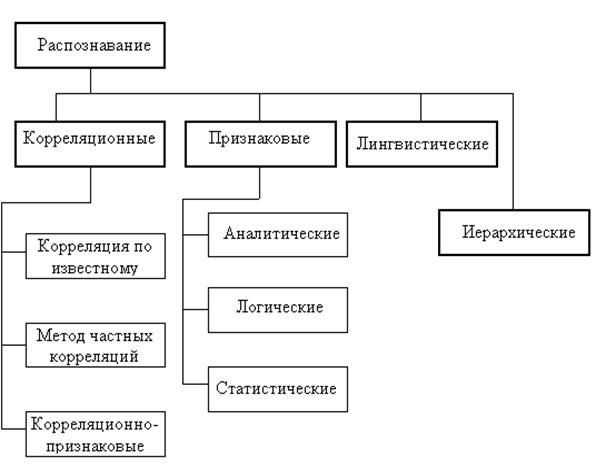
Схема 1. Классификация методов распознавания.
Рассмотрим три группы, относящихся к группе признаковых:
- Логические.
Системы
из этой подгруппы используют бинарное представление признаков, то есть
признак может принимать только два значения :0 или 1. В этом же
заключается основной недостаток подобных систем, так как два образа с
выраженностью произвольного признака равной 0,6 и 0,9 будут
представлены координатой 1. Основное преимущество логических
систем в их быстродействии.
- Аналитические.
Системы
из этой подгруппы характеризуются набором формул и критериев. Основной
недостаток систем этой группы - отсутствие единого методического
подхода к построению аналитической части. Преимуществом систем
этой группы является возможность адаптации к используемому виду и
размерности данных соответствующих аналитических выражений.
- Статистические.
Системы
из этой подгруппы используют статистические оценки (среднее значение,
дисперсию, статистические критерии и так далее) для реализации
процесса классификации. Основной недостаток систем этой группы -
зависимость результатов от качества используемых данных. Основное
преимущество - при достоверных и однородных данных получается
высокий уровень надежности результатов.[5,6]
АНАЛИТИЧЕСКИЕ МЕТОДЫ
В работе для распределения по классам используются аналитические методы распознавания. Рассмотрим подробно эту группу методов.
Метод обобщенного портрета. Его особенности:
- метод
обобщенного портрета полагает наличие характеристической точки в
пространстве признаков, в координатах которой обобщены признаки
конкретного класса;
- в
методе обобщенного портрета обязательно наличие некоторой области
(области обобщения) вокруг характеристической точки. Эта область и
является искомым классом;
- вариантом метода является случай, когда характеристическую точку не указывают, а область, занимаемую классом, отграничивают.
Варианты метода обобщенного портрета:
- В
качестве характеристической точки выбирается
статистическое
значение (среднее значение). Тогда область обобщения – это
гиперсфера с центром в характеристической точке и радиусом, равным
расстоянию от характеристической точки до самого дальнего
«представителя множества».
- Характеристическая
точка представлена в распределенном виде, то есть для каждого признака
существуют экстремальные его значения (максимальное, минимальное),
совокупность этих экстремумов заменяют собой характеристическую точку.
Таким образом, область обобщения – гиперпараллелепипед, размеры
ребер которого равны размаху минимум – максимум по
соответствующему признаку.
- Характеристическая
точка не указывается, а область отграничивается. Необходимое
отграничение области выполняется следующим образом: из всего множества
точек отбираются те, для каждой которых существуют 2 прямые,
соединяющие эту точку с двумя другими точками класса. Причем эти прямые
расположены так, что все точки рассматриваемого класса расположены по
одну сторону от прямой. В результате вокруг класса можно построить
оболочку из отрезков этих прямых. Эта оболочка будет отделять внешний
класс от внутреннего. Справедливо и для отделения внешних точек. [7]
Алгоритмы
метода обобщенного портрета реализуют идею минимизации эмпирического
риска в классе линейных и кусочно-линейных функций.
В общем
случае метод обобщенного портрета состоит в специальном способе
построения разделяющей гиперплоскости. В случае если обучающая
последовательность может быть разделена гиперплоскостью, существует
целое семейство разделяющих гиперплоскостей. Особенность метода
заключается в том, что с его помощью строится оптимальная
разделяющая гиперплоскость (то есть гиперплоскость, которая из
всех разделяющих гиперплоскостей наиболее далеко отстоит от ближайшего
к ней элемента последовательности). Важной особенностью метода
обобщенного портрета является возможность установить (в случае,
если это так), что «безошибочного» разделения элементов
последовательности не существует.[4]
Метод построения разделяющей гиперплоскости. Построение
разделяющей гиперплоскости используется для определения принадлежности
объекта к тому или иному классу образов. Рассмотрим этапы построения
разделяющей гиперплоскости.
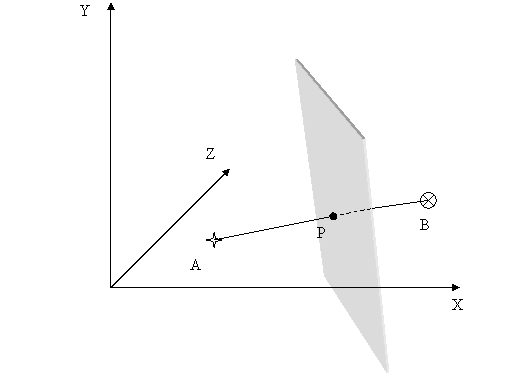
Рисунок 1. Построение разделяющей гиперплоскости.
На рисунке 1 схематически изображен процесс построения разделяющей
гиперплоскости. Нам известны координаты двух точек(объектов): A,B.
Которые представлены на рисунке в виде звездочки (точка А), и в виде
кружочка (точка В). Необходимо построить разделяющую гиперплоскость,
которая отделяла бы образы «похожие» на А, от образов
«похожих» на В.
Для построения, нам необходимо провести между точками А и В,
соединяющую их линию. На середине этой линии отложим точку Р, через
которую будет проходить разделяющая гиперплоскость. Теперь, зная
координаты точки Р, а также имея вектор АВ, построить плоскость,
проходящую через точку Р, и перпендикулярную вектору АВ. Теперь чтобы
принять решение о принадлежности образа к тому или иному классу, нужно
определить расстояние от этого образа до гиперплоскости, кроме того,
знак полученного расстояния будет говорить о положении образа с одной
или другой стороны от гиперплоскости.
Опишем общее уравнение плоскости:
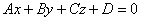
Тогда
исходя из уравнения плоскости, проходящей через точку, P(x1,y1,z1),
перпендикулярно прямой с направляющим вектором N(A,B,C):
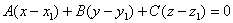
находим коэффициентD
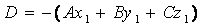
Где вектор N(A,B,C) – перпендикулярен к плоскости. Направляющие косинусы этого вектора:
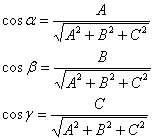
Подставляя эти значения в формулу для нахождения расстояния от
точки М(a,b,c) до плоскости:
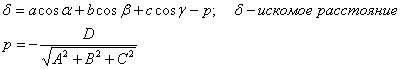
Получаем:
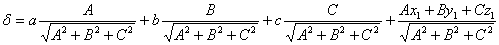
Разделяющая гиперплоскость не может быть построена без базисных точек. В качестве базисных точек могут быть выбраны:
- наугад взятые точки , по одной из множества А и множества В;
- точки, выбранные из А и В с учетом определенных
обстоятельств (например, имеющие минимальные расстояния между собой);
- точки, выбранные на основании каких-либо статистических характеристик.
Пусть нам даны множества А и В, каждое из которых состоит из 5 элементов (рисунок 2):

Рисунок 2. Разделение классов А и В гиперплоскостью
В качестве базисных точек выберем точки, координаты которых являются
средними арифметическими значениями соответствующие координат точек
каждого класса.
В качестве разделяющей классы А и В гиперплоскости выберем следующую плоскость:
R(х,у) = 2(Асред Всред)*Р+| Bсред |2-|Aсред|2 = 0, это векторное уравнение.
Отметим, что все расстояния точек Ai от гиперплоскости отрицательны:
Все расстояния точек Вi от разделяющей гиперплоскости положительны
Следовательно, R(x,y) разделяет множества А и В и если добавить новый
элемент в В, то такое расстояние будет положительно.
Существуют модификации данного метода, более сложные и основываются на
построении градиента. [7,4]
Метод "ФОРЕЛЬ"
относится к аналитическим методам. В методе используется критерий,
оценивающий плотность распределений образов в объеме, ограниченном
сферой фиксированного радиуса. При переходе от шага к шагу центр этой
сферы движется в сторону увеличения плотности точек – образов
(рисунок 3). Сфера стабилизируется в определенном положении, когда
плотность точек внутри ее становится максимальной, и любое перемещение
сферы ведет к ухудшению ситуации. Точки-образы, попадающие внутрь
стабилизировавшейся сферы, образуют класс N1. Процесс повторяется с
любой точки из оставшихся и завершается новой стабилизацией сферы,
внутри которой находится класс N2 и так далее. Количество классов,
получаемых при использовании метода, связано с величиной радиуса сферы.

Рисунок 3. Процесс перемещения формального элемента (сферы) по множеству объектов.[5]
Алгоритм. Задается радиус сферы R.
1-й шаг.
Строится сфера радиуса R с центром в любой точке так, чтобы внутрь
среды попала хотя бы одна точка - образ ZI. Определяется центр сферы.
Этот центр назовем C(1).
2-й шаг.
Определяются точки - образы ZI(1), для которых | ZI(1) - CI(1) | <R
т.е. эти точки попадают внутрь сферы.
3-й шаг.
Вычисляется центр тяжести таких ZI(1).
Если внутрь сферы попало k точек, то координаты центра тяжести 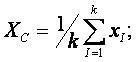 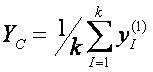
Этот центр тяжести назовем С(2)
4-й шаг.
Строится сфера радиуса R с центром в точке С(2).
Определяются точки ZI(2), для которых | ZI(2) - CI(2) | <R.
5-й шаг.
Вычисляется центр тяжести таких ZI(2); этот центр тяжести назовем С(3) и так далее.
Процесс "движения" среды, т.е. переход от С(k) к С(k+1)
останавливается тогда, когда расстояние | С(k) - С(k+1) | < .
Сфера с центром в С(k+1) представляет собой таксон S1.
6-й шаг.
Точки - образы I S1 из рассмотрения исключаются. В качестве начальной
берётся любая точка - образ из оставшихся, и процесс продолжается
с шага 1.
7-й шаг.
Последовательность таксонов S1, S2, ...., является последовательностью
классов P1, P2, ..., соответствующих радиусу сферы = R.
Замечание. Минимум суммарного объема сфер - таксонов дает рациональное разбиение набора образов на классы.
При всей своей наглядности и интерпретируемости результатов алгоритм
«Форель» обладает существенным недостатком: результаты
таксономии в большинстве случаев зависят от начального выбора центра
гиперсферы и ее радиуса. Существуют различные приёмы, уменьшающие эту
зависимость, но радикального решения этой задачи нет.
Метод дробящихся эталонов. Для
построения решающих правил нужна обучающая выборка. Обучающая
выборка – это множество объектов, заданных значениями
признаков и принадлежность которых к тому или иному классу достоверно
известна "учителю" и сообщается учителем "обучаемой" системе. По
обучающей выборке система строит решающие правила. Качество решающих
правил оценивается по контрольной (экзаменационной) выборке, в которую
входят объекты, заданные значениями признаков, и принадлежность которых
тому или иному образу известна только "учителю".
Метод построения эталонов. Для каждого класса по обучающей выборке строится эталон, имеющий значения признаков
 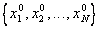 , ,
где 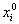 = =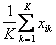 , ,
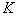 – количество объектов данного образа в обучающей выборке, – количество объектов данного образа в обучающей выборке,
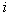 – номер признака. – номер признака.
По существу, эталон – это усреднённый по обучающей выборке
абстрактный объект (рисунок 5). Абстрактным мы его называем
потому, что он может не совпадать не только ни с одним объектом
обучающей выборки, но и ни с одним объектом генеральной совокупности.
Распознавание осуществляется следующим образом. На вход системы поступает объект 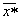 ,
принадлежность которого к тому или иному образу системе неизвестна. От
этого объекта измеряются расстояния до эталонов всех образов, и ,
принадлежность которого к тому или иному образу системе неизвестна. От
этого объекта измеряются расстояния до эталонов всех образов, и 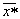 система
относит к тому образу, расстояние до эталона которого минимально.
Расстояние измеряется в той метрике, которая введена для решения
определённой задачи распознавания. система
относит к тому образу, расстояние до эталона которого минимально.
Расстояние измеряется в той метрике, которая введена для решения
определённой задачи распознавания.

Рисунок 5. Решающее правило "Минимум расстояния
до эталона класса":
Процесс обучения состоит в следующем. На первом этапе в обучающей
выборке " охватывают " все объекты каждого класса гиперсферой возможно
меньшего радиуса. Сделать это можно, например, так. Строится эталон
каждого класса. Вычисляется расстояние от эталона до всех объектов
данного класса, входящих в обучающую выборку. Выбирается максимальное
из этих расстояний 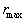 . Строится гиперсфера с центром в эталоне и радиусом . Строится гиперсфера с центром в эталоне и радиусом 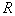 = =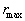 + +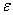 .
Она охватывает все объекты данного класса. Такая процедура проводится
для всех классов (образов). На рисунке 6 приведён пример двух
образов в двухмерном признаковом пространстве. .
Она охватывает все объекты данного класса. Такая процедура проводится
для всех классов (образов). На рисунке 6 приведён пример двух
образов в двухмерном признаковом пространстве.

Рисунок 6. Решающее правило типа «Метод дробящихся эталонов».
Если гиперсферы различных образов пересекаются и в области перекрытия
оказываются объекты более чем одного образа, то для них строятся
гиперсферы второго уровня, затем третьего до тех пор, пока
области не окажутся непересекающимися, либо в области пересечения будут
присутствовать объекты только одного образа.
Распознавание осуществляется следующим образом. Определяется
местонахождение объекта относительно гиперсфер первого уровня. При
попадании объекта в гиперсферу, соответствующую одному и только одному
образу, процедура распознавания прекращается. Если же объект оказался в
области перекрытия гиперсфер, которая при обучении содержала объекты
более чем одного образа, то переходим к гиперсферам второго уровня и
проводим действия такие же, как для гиперсфер первого уровня. Этот
процесс продолжается до тех пор, пока принадлежность неизвестного
объекта тому или иному образу не определится однозначно. Правда, это
событие может и не наступить. В частности, неизвестный объект может не
попасть ни в одну из гиперсфер какого-либо уровня. В этих случаях
"учитель" должен включить в решающие правила соответствующие действия.
Например, система может либо отказаться от решения об однозначном
отнесении объекта к какому-либо образу, либо использовать критерий
минимума расстояния до эталонов данного или предшествующего уровня.
Какой из этих приёмов эффективнее, сказать трудно, так как метод
дробящихся эталонов носит в основном эмпирический характер.[4,5]
Метод k-внутригрупповых средних.
Опишем алгоритм:
1 шаг. Выбирается К исходных центров 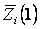 будущих кластеров, например, первые К-образов. будущих кластеров, например, первые К-образов. 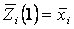 , где i=(1,2, …, K). , где i=(1,2, …, K).
2 шаг. Вычисляется матрица расстояний между объектами и выбранными центрами классов по евклидовой метрике.
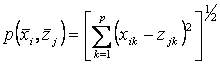 , ,
где : 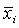 - объект, характеризующийся набором признаков; - объект, характеризующийся набором признаков;
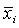 = ( = (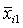 , ,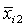 , …, , …, 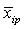 ) - (i=1, 2, …, n), ) - (i=1, 2, …, n),
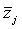 = ( = (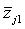 , ,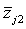 , …, , …, 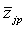 ) - (j=1, 2, …, K), ) - (j=1, 2, …, K),
n-количество объектов, p – количество признаков.
3 шаг. Распределяются объекты 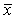 по классам по классам 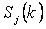 на k-том шаге итерации по следующему правилу: на k-том шаге итерации по следующему правилу:
 , если , если 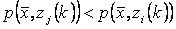 для всех i=(1,2, …, K), для всех i=(1,2, …, K), 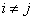 , где , где 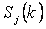 - множество объектов j-того класса с центром - множество объектов j-того класса с центром 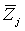 . В случае равенства расстояний элемент . В случае равенства расстояний элемент 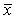 относится к классу, имеющему меньший порядковый номер. относится к классу, имеющему меньший порядковый номер.
4 шаг. Корректируем центры классов, то есть вычисляются новые центры классов по формуле:
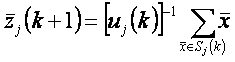
где 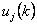 - число объектов, входящих в класс - число объектов, входящих в класс 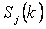 . .
5 шаг. Проверяем сходимость алгоритма, то есть равенства
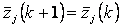 (j=1, 2, …, K). (j=1, 2, …, K).
Если это равенство выполняется, то процедура нахождения классов
заканчивается. В противном случае осуществляется переход к следующей
итерации, то есть алгоритм повторяется с шага 2.
Качество работы алгоритма зависит от:
- числа выбираемых центров класса;
- координат центров классов;
- геометрических особенностей расположения данных в евклидовом пространстве;
- выбранной меры близости (сходства) между объектами.[9]
|