Тема 5. Нейронные сети

Биологический нейрон

Центральная нервная система имеет клеточное строение. Единица – нервная клетка, нейрон. Нейрон имеет следующие основные свойства:
1. Участвует в обмене веществ и рассеивает энергию. Меняет внутреннее состояние с течением времени, реагирует на входные сигналы и формирует выходные воздействия и поэтому       является активной динамической системой.
2. Имеет множество синапсов – контактов для передачи информации.
3. Нейрон взаимодействует путем обмена электрохимическими сигналами двух видов:   электротоническими  (с затуханием) и нервными импульсами (спайками), распространяющимися без затухания.

Биологический нейрон содержит следующие структурные единицы (рис.1):
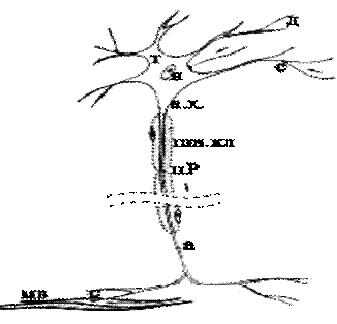рис.1 Биологический нейрон
Тело клетки (т) — сома: содержит ядро (я), митохондрии (обеспечивают клетку энергией), другие органеллы, поддерживающие жизнедеятельность клетки.
Дендриты (д) – входные волокна, собирают информацию от других нейронов. Активность в дендритах меняется плавно. Длина их обычно не больше 1 мм.
Мембрана – поддерживает постоянный состав цитоплазмы внутри клетки, обеспечивает проведение нервных импульсов.
Цитоплазма — внутренняя среда клетки.
Аксон (а), один или ни одного у каждой клетки, – длинное, иногда больше метра, выходное нервное волокно клетки. Импульс генерируется в лоном холмике (а.х.). Аксон обеспечивает проведение импульса и передачу воздействия на другие нейроны или мышечные волокна (мв). Ближе к концу аксон часто ветвится.
Синапс (с) – место контакта нервных волокон — передает возбуждение от клетки к клетке. Передача через синапс почти всегда однонаправленная. Различают пресинаптические и постсинаптические клетки — по направлению передачи импульса.
Шванновские клетки (шв.кл). Специфические клетки, почти целиком состоящие из миелина, органического изолирующего вещества. Плотно «обматывают» нервное волокно 250 слоями миелина. Неизолированные места нервного волокна между шванновскими клетками называются перехватами Ранвье (пР). За счет миелиновой изоляции скорость распространения нервных импульсов возрастает в 5-10 раз и уменьшаются затраты энергии на проведение импульсов. Миелинизированные волокна встречаются только у высших животных.
В центральной нервной системе человека насчитывается от 100 до 1000 типов нервных клеток, в зависимости выбранной степени детализации. Они отличаются картиной дендритов, наличием и длиной аксона и распределением синапсов около клетки.
Клетки сильно связаны между собой. У нейрона может быть больше 1000 синапсов. Близкие по функциям клетки образуют скопления, шаровидные или параллельные слоистые. В мозгу выделены сотни скоплений. Кора головного мозга – тоже скопление. Толщина коры — 2 мм, площадь — около квадратного фута [5].

Формальный нейрон

Биологический нейрон — сложная система, математическая модель которого до сих пор полностью не построена. Введено множество моделей, различающихся вычислительной сложностью и сходством с реальным нейроном. Одна из важнейших — формальный нейрон (рис.1).  Несмотря на простоту ФН, сети, построенные из таких нейронов, могут сформировать произвольную многомерную функцию на выходе.
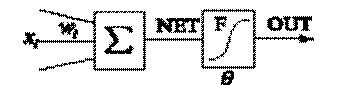рис. 1  Формальный нейрон
Нейрон состоит из взвешенного сумматора и нелинейного элемента.
Функционирование нейрона определяется формулами:
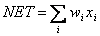          (1)                    OUT= F(NET)           (2)
где xi — входные сигналы, совокупность всех входных сигналов нейрона образует вектор x;
w i — весовые коэффициенты, совокупность весовых коэффициентов образует вектор весов w;
NET — взвешенная сумма входных сигналов, значение NET передается на нелинейный элемент;

— пороговый уровень данного нейрона;
F — нелинейная функция, называемая функцией активации (функция преобразования).
Нейрон имеет несколько входных сигналов x и один выходной сигнал OUT. Параметрами нейрона, определяющими его работу, являются: вектор весов w, пороговый уровень ?и вид функции активации F.
Функционирование нейрона происходит следующим образом.
В текущий момент времени через входные синапсы  на нейрон направляются сигналы от других нейронов и/или из внешнего мира. Каждый синапс имеет параметр, называемый весом синапса, и представляющий какое-либо число. Сигнал, проходящий через синапс, умножается на вес этого синапса. В зависимости от веса, сигнал может быть усилен (модуль веса > 1) или ослаблен (модуль веса < 1) по амплитуде. Сигналы от всех синапсов, ведущих к данному нейрону, принимает сумматор.
Сумматор производит суммирование всех пришедших сигналов и подает на собственно нейрон (преобразователь) одно число - полученную сумму. Величина этого числа будет зависеть как от величин исходных сигналов, так и от весов синапсов. Нейрон, получивший это число, преобразует его согласно своей функции, в результате которой получается другое число, и отправляет его по "аксону" всем остальным нейронам через соответствующие синапсы. Последующие нейроны производят с полученными сигналами такие же операции, лишь с тем различием, что во-первых, веса их синапсов могут быть уже другими, во-вторых, другие нейроны могут иметь другой вид функции преобразования [10].

Виды функций активации

Основные виды функций активации, получившие распространение в искусственных НС.
1. Жесткая ступенька :
     
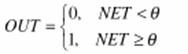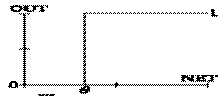
Используется в классическом формальном нейроне. Развита полная теория, позволяющая синтезировать произвольные логические схемы на основе ФН с такой нелинейностью. Функция вычисляется двумя-тремя машинными инструкциями, поэтому нейроны с такой нелинейностью требуют малых вычислительных затрат.
Эта функция чрезмерно упрощена и не позволяет моделировать схемы с непрерывными сигналами. Отсутствие первой производной затрудняет применение градиентных методов для обучения таких нейронов.
2. Логистическая функция (сигмоида, функция Ферми):
                
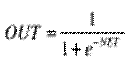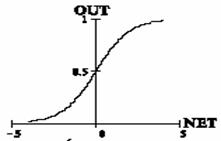
Применяется очень часто для многослойных перцептронов и других сетей с непрерывными сигналами. Гладкость, непрерывность функции — важные положительные качества. Непрерывность первой производной позволяет обучать сеть градиентными методами (например, метод обратного распространения ошибки).
Функция симметрична относительно точки (NET=0, OUT=1/2), это делает равноправными значения OUT=0 и OUT=1, что существенно в работе сети. Тем не менее, диапазон выходных значений от 0 до 1 несимметричен, из-за этого обучение значительно замедляется.
Данная функция — сжимающая, т.е. для малых значений NET коэффициент передачи K=OUT/NET велик, для больших значений он снижается. Поэтому диапазон сигналов, с которыми нейрон работает без насыщения, оказывается широким.
Значение производной легко выражается через саму функцию. Быстрый расчет производной ускоряет обучение.
Выбор функции активации определяется:
1. Спецификой задачи.
2. Удобством реализации на ЭВМ, в виде электрической схемы или другим способом.
3. Алгоритмом обучения: некоторые алгоритмы накладывают ограничения на    вид функции активации, их нужно учитывать.
Чаще всего вид нелинейности не оказывает принципиального влияния на решение задачи. Однако удачный выбор может сократить время обучения в несколько раз  [5].
Итак, модель формального нейрона не является биоподобной и скорее похожа на математическую абстракцию, чем на живой нейрон. Тем удивительнее оказывается многообразие задач, решаемых с помощью таких нейронов и универсальность получаемых алгоритмов.

Искусственные нейронные сети

Искусственные нейронные сети (НС) — совокупность моделей биологических нейронных сетей. Представляют собой сеть элементов — искусственных нейронов — связанных между собой синаптическими соединениями. Сеть обрабатывает входную информацию и в процессе изменения своего состояния во времени формирует совокупность выходных сигналов.
Работа сети состоит в преобразовании входных сигналов во времени, в результате чего меняется внутреннее состояние сети и формируются выходные воздействия. Обычно НС оперирует цифровыми, а не символьными величинами.
Большинство моделей НС требуют обучения. В общем случае, обучение — такой выбор параметров сети, при котором сеть лучше всего справляется с поставленной проблемой. Обучение — это задача многомерной оптимизации, и для ее решения существует множество алгоритмов.
Искусственные нейронные сети — набор математических и алгоритмических методов для решения широкого круга задач. Выделим характерные черты искусственных нейросетей как универсального инструмента для решения задач:
1. НС дают возможность лучше понять организацию нервной системы человека и животных на средних уровнях: память, обработка сенсорной информации, моторика.
2.  НС — средство обработки информации:
а) гибкая модель для нелинейной аппроксимации многомерных функций;
б)  средство прогнозирования во времени для процессов, зависящих
от многих переменных;
в) классификатор по многим признакам, дающий разбиение входного пространства на области;
г) средство распознавания образов;
д) инструмент для поиска по ассоциациям;
е) модель для поиска закономерностей в массивах данных.
3. НС свободны от ограничений обычных компьютеров благодаря параллельной обработке и сильной связанности нейронов.
4. В перспективе НС должны помочь понять принципы, на которых построены  высшие функции нервной системы: сознание, эмоции, мышление.

Современные искусственные НС по сложности и "интеллекту" приближаются к нервной системе таракана, но уже сейчас демонстрируют ценные свойства:
1. Обучаемость. Выбрав одну из моделей НС, создав сеть и выполнив алгоритм обучения, мы можем обучить сеть решению задачи, которая ей по силам. Нет никаких гарантий, что это удастся сделать при выбранных сети, алгоритме и задаче, но если все сделано правильно, то обучение бывает успешным.
2. Способность к обобщению. После обучения сеть становится нечувствительной к малым      изменениям входных сигналов (шуму или вариациям входных образов) и дает правильный результат на выходе.
3. Способность к абстрагированию. Если предъявить сети несколько искаженных вариантов входного образа, то сеть сама может создать на выходе идеальный образ, с которым она никогда не встречалась.

Архитектура нейронной сети

Основой работы самообучающихся нейропрограмм является нейронная сеть, представляющая собой совокупность нейронов - простых элементов, связанных между собой определенным образом. Нейроны и межнейронные связи задаются программно на обычном компьютере или могут иметь "материальную" основу - особую микросхему (нейрочип), которые применяются в специально созданных нейрокомпьютерах. Структура взаимосвязей между нейронами в нейрокомпьютере или нейропрограмме аналогична таковой в биологических объектах. Искусственный нейрон имеет коммуникации с другими нейронами через синапсы, передающие сигналы от других нейронов к данному (дендриты) или от данного нейрона к другим (аксон). Кроме того, нейрон может быть связан сам с собой. Несколько нейронов, связанных между собой определенным образом, образуют нейронную сеть [10].
Нейросеть, также как и биологический аналог, должна иметь каналы для связи с внешним миром. Одни каналы обеспечивают поступление информации из внешнего мира на нейросеть, другие выводят информацию из нейросети во внешний мир. Поэтому одни нейроны сети рассматривается как входные, другие же - как выходные. Часть нейронов может не сообщаться с внешним миром, а взаимодействовать с входными, выходными и такими же нейронами ("скрытые" нейроны).
Очевидно, что существует огромное количество способов соединения нейронов, растущее с увеличением числа нейронов в сети. Наиболее употребительной является слоистая архитектура (рис.3), в которой нейроны располагаются “слоями”. В наиболее общем случае аксоны каждого нейрона одного слоя направлены к нейронам следующего слоя. Таким образом, нейроны первого слоя являются входными (принимающими информацию из внешнего мира), нейроны последнего слоя - выходными (выдающими информацию во внешний мир).

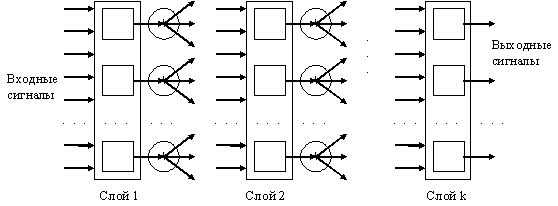
Рис. 3. Слоистая сеть

Число нейронов в каждом слое может быть любым и никак заранее не связано с количеством нейронов в других слоях. Стандартный способ подачи входных сигналов: все нейроны первого слоя получают каждый входной сигнал. Особое распространение получили трехслойные сети, в которых каждый слой имеет свое наименование: первый – входной, второй – скрытый, третий – выходной [3].
Другой вид архитектуры - полносвязная, когда каждый нейрон соединен с каждым, в том числе сам с собой. Пример простейшей нейросети из 3 нейронов показан на рис. 4. Для удобства изображения из каждого нейрона выходит не один, а несколько аксонов, направленных на другие нейроны или во внешний мир, что аналогично присоединенным к одному аксону через синапсы нескольким дендритам.

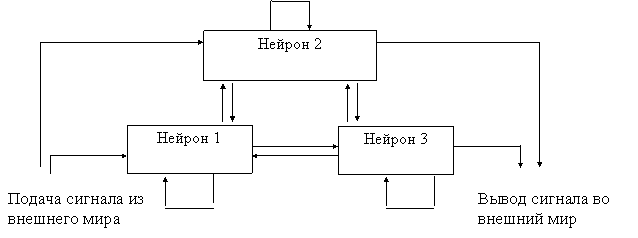
Рис. 4. Схема простейшей нейронной сети из 3 нейронов. Сеть имеет 13 синапсов, 4 из которых служат для связи с внешним миром, а остальные соединяют нейроны между собой

Слоистая или полносвязная архитектуры не налагают существенных ограничений на участвующие в них элементы. Единственное жесткое требование, предъявляемое архитектурой к элементам сети, это соответствие размерности вектора входных сигналов элемента (она определяется архитектурой) числу его входов.
Если полносвязная сеть функционирует до получения ответа заданное число тактов k, то ее можно представить как частный случай k-слойной сети, все слои которой одинаковы и каждый из них соответствует такту функционирования полносвязной сети.
Существенное различие между полносвязной и слоистой сетями возникает тогда, когда число тактов функционирования заранее не ограничено – слоистая сеть так работать не может.

Функционирование нейросети

            В случае эмуляции нейросети на обычном компьютере все математические операции осуществляет программа. Нейронная сеть при этом представляет собой массив синаптических весов. Этот массив может находиться либо на диске компьютера в виде файла определенного формата (при хранении нейросети) либо в оперативной памяти компьютера (когда нейросеть функционирует).
При создании новой нейросети в памяти компьютера отводится место под массив синаптических весов, называемый картой. Этот массив заполняется совершенно случайными числами из определенного диапазона. Поэтому каждая созданная сеть даже при одних и тех же параметрах (число нейронов, их характеристика) является уникальной. Уникальность сетей проявляется в том, что сети с одинаковыми параметрами, обучающиеся на одинаковых задачах, ведут себя неодинаково. Это касается времени обучения, качества обучения, уверенности в выдаваемых ответах при тестировании. В этом еще одно сходство сетей с биообъектами.
Рассмотрим работу сети безотносительно к процессу обучения или выдачи решения. После инициализации сети веса всех синапсов случайны. В начальный момент времени на входные нейроны через входные синапсы (один или несколько) подается из внешнего мира вектор входных сигналов, представляющий набор чисел (или одно число). Далее этот сигнал начинает распространяться по всем связям между нейронами, изменяясь при прохождении через каждый нейрон согласно схеме функционирования нейрона. В конечном итоге, после одного прохода выходные нейроны выдадут во внешний мир какие-либо сигналы. Вся процедура однократного прохождения сигналов по нейронной сети является тактом функционирования сети. Можно не считывать сигналы с выходных нейронов после одного такта функционирования, а продолжить обмен сигналами еще несколько раз, не подавая сигналов на вход. Обычно количество тактов функционирования между подачей сигналов на вход и снятием сигналов с выхода фиксировано для данной сети. Как правило, этот параметр задается при инициализации сети и хранится в файле сети вместе с матрицей коэффициентов (как и некоторые другие параметры - число нейронов, характеристика нейронов и т.д.).
Таким образом, нейронная сеть, получающая на входе некоторый сигнал, способна после прохода его по нейронам выдавать на выходе определенный ответ, который зависит от весовых коэффициентов всех нейронов и от самого сигнала. Очевидно, что при осуществлении таких процедур на только что инициализированной сети мы будем получать на выходе сигналы, лишенные всякого смысла (весовые коэффициенты случайны). Чтобы добиться выдачи сетью требуемого результата, необходимо обучить ее [2].

Общая схема обучения нейронной сети

Алгоритмы обучения бывают с учителем и без. Алгоритм называется алгоритмом с учителем, если при обучении известны и входные, и выходные вектора сети. Имеются пары вход + выход — известные условия задачи и решение. В процессе обучения сеть меняет свои параметры и учится давать нужное отображение X Y. Сеть учится давать результаты, которые нам уже известны. За счет способности к обобщению сетью могут быть получены новые результаты, если подать на вход вектор, который не встречался при обучении.

Обучение с учителем

Для обучения нейронной сети с учителем необходима обучающая выборка (задачник), состоящая из примеров. Каждый пример представляет собой задачу одного и того же типа с индивидуальным набором условий (входных параметров) и заранее известным ответом. Например, в качестве входных параметров в одном примере могут использоваться данные обследования одного больного, тогда заранее известным ответом в этом примере может быть диагноз. Несколько примеров с разными ответами образуют задачник. Задачник располагается в базе данных, каждая запись которой является примером [1].
Общая схема обучения нейросети с учителем:

1. Из обучающей выборки берется текущий пример (изначально, первый) и его входные параметры (представляющие в совокупности вектор входных сигналов) подаются его на входные синапсы обучаемой нейросети. Обычно каждый входной параметр примера подается на один соответствующий входной синапс.
2. Нейросеть производит заданное количество тактов функционирования, при этом вектор входных сигналов распространяется по связям между нейронами (прямое функционирование).
3. Измеряются сигналы, выданные теми нейронами, которые считаются выходными.
4. Производится интерпретация выданных сигналов, и вычисляется оценка, характеризующая различие между выданным сетью ответом и требуемым ответом, имеющимся в примере. Оценка вычисляется с помощью соответствующей функции оценки. Чем меньше оценка, тем лучше распознан пример, тем ближе выданный сетью ответ к требуемому. Оценка, равная нулю, означает что требуемое соответствие вычисленного и известного ответов достигнуто. Заметим, что только что инициализированная (необученная) нейросеть может выдать правильный ответ только совершенно случайно.
5. Если оценка примера равна нулю, ничего не предпринимается. В противном случае на основании оценки вычисляются поправочные коэффициенты для каждого синаптического веса матрицы связей, после чего производится подстройка синаптических весов (обратное функционирование). В коррекции весов синапсов и заключается обучение.
6. Осуществляется переход к следующему примеру задачника и вышеперечисленные операции повторяются. Проход по всем примерам обучающей выборки с первого по последний считается одним циклом обучения.

            При прохождении цикла каждый пример имеет свою оценку. Вычисляется, кроме того, суммарная оценка множества всех примеров обучающей выборки. Если после прохождения нескольких циклов она равна нулю, обучение считается законченным, в противном случае циклы повторяются.
Количество циклов обучения, также как и время, требующееся для полного обучения, зависят от многих факторов - величины обучающей выборки, количества входных параметров, вида задачи, типа и параметров нейросети и даже от случайного расклада весов синапсов при инициализации сети [3].

Обучение без учителя

Алгоритм относится к обучению без учителя, если известны только входные вектора, и на их основе сеть учится давать наилучшие значения выходов. Что понимается под “наилучшими” — определяется алгоритмом обучения.
Для алгоритмов обучения с учителем нужны известные входные и выходные вектора, а эта информация не всегда доступна.
Вопрос о биологической правдоподобности обучения с учителем также открыт. Нейроны зрительной коры, например, учатся реагировать на световые импульсы лишь под действием самих импульсов, без внешнего учителя. Однако высшие этапы обучения, например, у детей, невозможны без "учителя" в лице его родителя. Кроме того, отдельные области в мозге вполне могут выполнять роль "учителей" для других, управляя их активностью. Поэтому нельзя однозначно сказать, какой тип обучения биологически правдоподобнее, с учителем или без.
При обучении без учителя сеть имеет для обучения лишь известные входные вектора. Правильные значения выходных векторов неизвестны. Какие вектора будут сформированы на выходе, зависит от алгоритма обучения. Обучающее множество состоит из S известных входных векторов xs  s =1... S, в процессе обучения сеть учится формировать выходные вектора ys для каждого вектора из обучающего множества xs.
Успех обучения во многом зависит от числа нейронов в сети, или, точнее, от числа синапсов. Именно весовые коэффициенты синапсов хранят "опыт" сети. Теоретически, бесконечно увеличивая число нейронов и синапсов, всегда можно добиться полного обучения сети на данном задачнике, однако это ли является целью создателя экспертной системы? Очевидно, нет. Главное, чтобы обученная сеть хорошо распознавала примеры, как раз не входящие в задачник.
Проблема заключается в том, что сеть с заведомо большим (избыточным) числом синапсов (относительно данного задачника) может хорошо обучиться, просто "механически запомнив" имеющиеся примеры. Такая сеть обучится быстро (нет необходимости как можно более точной подстройки весов) за счет количества, а не качества.
Хорошим практическим выходом из данной затруднительной ситуации были бы сети, способные автоматически наращивать число нейронов при невозможности дальнейшего обучения, не теряя при этом уже имеющегося опыта [1].

  Классификация нейронных сетей

 Однослойный перцептрон

Круг проблем, которые под силу однослойному перцептрону, очень ограничен. Рассмотрим однослойную сеть из одного нейрона (рис 5).
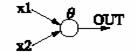Рис.5  Сеть из одного нейрона.
Выход сети: y = F(w1x1+w2x2). Если F имеет вид жесткой ступеньки с двумя возможными значениями, 0 и 1, то выход сети будет иметь вид (рис. 6). Гиперплоскость (в случае многих входов), разделяющая различные значения выхода, называется решающей поверхностью. Для жесткой ступеньки решающая поверхность задается уравнением:                        w1x1+w2x2
Рис.6 Возможный выход, если F имеет вид жесткой ступеньки
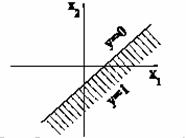Для двухвходового нейрона она имеет вид прямой, произвольно повернутой и смещенной из начала координат. Угол поворота определяется коэффициентами  w1, w2, а смещение из начала
координат — порогом.
Если выбрана гладкая функция активации, то выход сети будет плавно меняться от нуля до единицы в направлении, перпендикулярном прямой. Зависимость выходного сигнала от входов удобно представлять полутоновой картой: черному цвету соответствует значение выхода, равное 0, белому — равное 1. По осям отложены значения входов. Реальная зависимость для функции активации в виде гиперболического тангенса — на рис.7 [5].

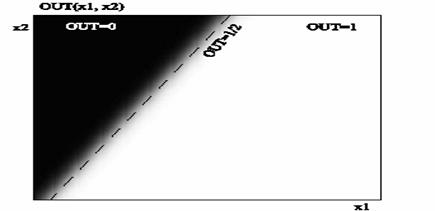
Рис.7  Выход однослойного перцептрона в виде полутоновой карты.

Многослойный перцептрон

Формальные нейроны могут объединяться в сети различным образом. Самым распространенным видом сети стал многослойный перцептрон (рис. 8).

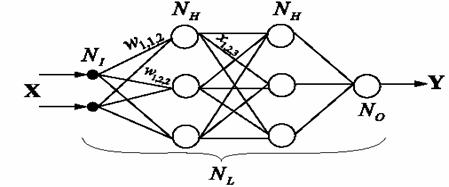
Рис.8 . Многослойный перцептрон.
Сеть состоит из произвольного количества слоев нейронов. Нейроны каждого слоя соединяются с нейронами предыдущего и последующего слоев по принципу "каждый с каждым". Первый слой (слева) называется сенсорным или входным, внутренние слои называются скрытыми или ассоциативными, последний (самый правый, на рисунке состоит из одного нейрона) — выходным или результативным. Количество нейронов в слоях может быть произвольным. Обычно во всех скрытых слоях одинаковое количество нейронов.
Обозначим количество слоев и нейронов в слое. Входной слой: NI нейронов; NH нейронов в каждом скрытом слое; NO выходных нейронов. x — вектор входных сигналы сети, y - вектор выходных сигналов.
Существует путаница с подсчетом количества слоев в сети. Входной слой не выполняет никаких вычислений, а лишь распределяет входные сигналы, поэтому иногда его считают, иногда — нет. Обозначим через NL полное количество слоев в сети, считая входной.
Работа многослойного перцептрона (МСП) описывается формулами:
                   
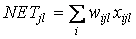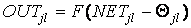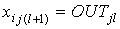
где индексом i всегда будем обозначать номер входа, j — номер нейрона в слое, l — номер слоя.
xijl — i-й входной сигнал j-го нейрона в слое l;
wijl — весовой коэффициент i-го входа нейрона номер j в слое l;
NETjl — сигнал NET j-го нейрона в слое l;   OUTjl — выходной сигнал нейрона;
?jl??— пороговый уровень нейрона j в слое l;
Введем обозначения: wjl — вектор-столбец весов для всех входов нейрона j в слое l; Wl — матрица весов всех нейронов в слоя l. В столбцах матрицы расположены вектора wjl . Аналогично x jl — входной вектор-столбец слоя l.
Каждый слой рассчитывает нелинейное преобразование от линейной комбинации сигналов предыдущего слоя. Отсюда видно, что линейная функция активации может применяется только для тех моделей сетей, где не требуется последовательное соединение слоев нейронов друг за другом. Для  многослойных сетей функция активации должна быть нелинейной, иначе можно построить эквивалентную однослойную сеть, и многослойность оказывается ненужной. Если применена линейная функция активации, то каждый слой будет давать на выходе линейную комбинацию входов. Следующий слой даст линейную комбинацию выходов предыдущего, а это эквивалентно одной линейной комбинации с другими коэффициентами, и может быть реализовано в виде одного слоя нейронов [5].
Многослойная сеть может формировать на выходе произвольную многомерную функцию при соответствующем выборе количества слоев, диапазона изменения сигналов и параметров нейронов.
Как и ряды, многослойные сети оказываются универсальным инструментом аппроксимации функций. Видно отличие работы нейронной сети от разложения функции в ряд:
 
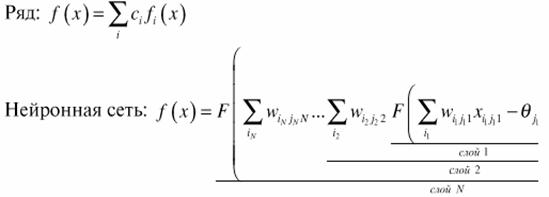
За счет поочередного расчета линейных комбинаций и нелинейных преобразований достигается аппроксимация произвольной многомерной функции при соответствующем выборе параметров сети.
В многослойном перцептроне нет обратных связей. Такие модели называются сетями прямого распространения. Они не обладают внутренним состоянием и не позволяют без дополнительных приемов моделировать развитие динамических систем [3].
Алгоритм решения задач с помощью МСП
Чтобы построить МСП, необходимо выбрать его параметры. Чаще всего выбор значений весов и  порогов требует обучения, т.е. пошаговых изменений весовых коэффициентов и пороговых уровней.
Общий алгоритм решения:
1. Определить, какой смысл вкладывается в компоненты входного вектора x. Входной вектор должен содержать формализованное условие задачи, т.е. всю информацию, необходимую для получения ответа.
2. Выбрать выходной вектор y таким образом, чтобы его компоненты содержали полный ответ поставленной задачи.
3. Выбрать вид нелинейности в нейронах (функцию активации). При этом желательно учесть специфику задачи, т.к. удачный выбор сократит время обучения.
4. Выбрать число слоев и нейронов в слое.
5. Задать диапазон изменения входов, выходов, весов и пороговых уровней, учитывая множество значений выбранной функции активации.
6. Присвоить начальные значения весовым коэффициентам и пороговым уровням и дополнительным параметрам (например, крутизне функции активации, если она будет настраиваться при обучении). Начальные значения не должны быть большими, чтобы нейроны не оказались в насыщении (на горизонтальном участке функции активации), иначе обучение будет очень медленным. Начальные значения не должны быть и слишком малыми, чтобы выходы большей части нейронов не были равны нулю, иначе обучение также замедлится.
7. Провести обучение, т.е. подобрать параметры сети так, чтобы задача решалась наилучшим образом. По окончании обучения сеть готова решить задачи того типа, которым она обучена.
8. Подать на вход сети условия задачи в виде вектора x. Рассчитать выходной вектор y, который и даст формализованное решение задачи.
Примеры  задач, решаемых с помощью МСП:
1. Задача классификации.
2. Распознавание букв алфавита.
3. Аппроксимация многомерной функции.
4. Синтез речи: NET-talk [5]
Сеть Кохонена
Задача классификации заключается в разбиении объектов на классы, когда основой разбиения служит вектор параметров объекта. Объекты в пределах одного класса считаются эквивалентными с точки зрения критерия разбиения. Сами классы часто бывают неизвестны заранее, а формируются динамически. Классы зависят от предъявляемых объектов, и поэтому добавление нового объекта требует корректирования системы классов [11].
Если для классификации применять нейронные сети, необходимо формализовать задачу. Самый очевидный способ: выберем в качестве входных данных вектор параметров единственного объекта. Результатом работы сети будет код класса, к которому принадлежит предъявленный на входе объект. В нейросетях принято кодирование номером канала. Поэтому сеть будет иметь M выходов, по числу классов, и чем большее значение принимает выход номер m0, тем больше "уверенность" сети в том, что входной объект принадлежит к классу m0 . Полезно применить функцию активации SOFTMAX, тогда сумма выходов всегда будет равна единице. Каждый выход можно будет трактовать как вероятность того, что объект принадлежит данному классу. Все выходы образуют полную группу, т.к. сумма выходов равна единице, и объект заведомо относится к одному из классов.
Выберем евклидову меру близости. В этом случае ядро класса, минимизирующее сумму мер близости для объектов этого класса, совпадает с центром тяжести объектов:
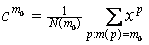           где N(m0)— число объектов x p в классе m0 .
При разбиении на классы должна быть минимизирована суммарная мера близости для всего множества  x p входных объектов.
Сеть нейронов, использующая евклидову меру близости для классификации объектов,  называется сетью Кохонена (рис. 9).
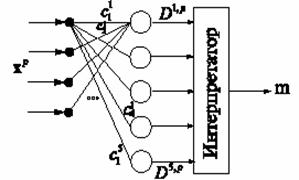Рис.9 . Сеть Кохонена
Нейроны слоя Кохонена генерируют сигналы Dm,p . Интерпретатор выбирает максимальный сигнал слоя Кохонена и выдает номер класса m, соответствующий номеру входа, по которому интерпретатором получен максимальный сигнал. Это соответствует номеру класса объекта, который был предъявлен на входе, в виде вектора x p .
Ядра cm являются весовыми коэффициентами нейронов. Каждый нейрон Кохонена запоминает одно ядро класса, и отвечает за определение объектов в своем классе, т.е. величина выхода нейрона тем больше, чем ближе объект к данному ядру класса. Общее количество классов совпадает с количеством нейронов Кохонена. Меняя количество нейронов, можно динамически менять количество классов [4].
Сеть Хопфилда
Для сетей прямого распространения были приняты ограничения: все сигналы в сети распространяются только от входа к выходу, но не наоборот. Сеть также предполагалась послойно - полносвязной. Оба эти ограничения несправедливы для биологических НС и сужают возможности модели. Сеть прямого распространения не имеет внутреннего состояния: значения выходов нейронов зависят только от входного вектора и не меняются во времени, если вход неизменен. Моделирование динамических процессов на таких сетях возможно только искусственными приемами, например, когда сетью на каждом шаге прогнозируется малое изменение состояния для исследуемого динамического объекта [10].
Чтобы расширить диапазон решаемых задач, были предложены сети с обратными связями. Полное математическое описание пока создано только для простейших случаев сетей с обратными связями. Дж. Хопфилд внес вклад в разработку и теории, и моделей таких сетей.
Рассмотрим однослойную сеть с обратными связями, где значение выхода каждого нейрона подается обратно на входы всех нейронов того же слоя (р. 10):
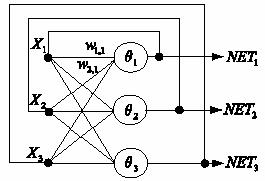Рис10 Сеть с обратными связями.
Входной вектор для сети в данном случае совпадает с выходным NET, взятым на предыдущей итерации. Предполагаем, что расчет сигналов NET происходит мгновенно и одновременно во всех нейронах, а распространение по обратным связям дает задержку в одну итерацию и происходит одновременно во всех нейронах: сеть работает синхронно. На каждой итерации по вектору X получается новый вектор NET, который отличается от X небольшим. Длина шага будет пропорциональна h - небольшому положительному числу, выбранного нами при создании сети.
Сформированный сигнал NET подается обратно на вход сети, и на следующей итерации становится новым значением X. Так, на каждой итерации происходит небольшое изменение вектора X в направлении антиградиента P, т.е. в сторону минимума многочлена P(x) [5].
Сети с обратными связями могут работать в качестве ассоциативной памяти. Это означает, что по вектору, поданному на вход, сетью будет создан на выходе один из запомненных ранее векторов, наиболее "похожий" (в некотором выбранном смысле) на данный входной вектор. Такой способ выборки данных называется адресацией по содержимому, в отличие от адресации по номеру ячейки памяти, принятому в ЭВМ фон-неймановского типа. Этот способ адресации широко используется в биологических НС. Например, один лишь запах жасмина может вызвать в памяти целый набор ассоциаций, причудливо связанных друг с другом и включающих в себя визуальные, звуковые и кинестетические образы. Память с такой адресацией является весьма перспективной для создания систем искусственного интеллекта, систем распознавания речевых сигналов и изображений [3].
Решение задач с помощью сетей Хопфилда
Решение некоторой задачи с помощью сетей Хопфилда распадается на этапы:
1. Построить функцию энергии таким образом, чтобы точка глобального минимума этой функции совпадала с решением задачи. При этом градиент функции энергии должен допускать вычисление с помощью НС.
2. Записать формулы для расчета параметров сети (весовых коэффициентов и пороговых уровней) для расчета градиента функции энергии.
3. Разорвать цепочку обратной связи и предъявить сети входной вектор. Рассчитать значения выходов.
4. Замкнуть обратную связь и предоставить сети возможность самостоятельно менять свое состояние (релаксация). Остановить процесс релаксации после того, как выходной вектор перестанет меняться, т.е. по достижении минимума функции энергии. Полученные выходы сети дают решение задачи [11].