Тема 6. Эвристические алгоритмы
Ещё со времён Ламарка развитие живого мира рассматривается как процесс постоянного совершенствования (приспособления) особей под влиянием среды. Моделируя отбор лучших планов, как процесс эволюции в популяции особей, можно получить решение задачи оптимизации, задав начальные условия эволюционного процесса, населив виртуальную вселенную существами — носителями информации и указав цель эволюционного процесса.
Природа поражает своей сложность и богатством всех своих проявлений. Среди примеров можно назвать сложные социальные системы, иммунные и нейронные системы, сложные взаимосвязи между видами. Они - всего лишь некоторые из чудес, которые стали более очевидны, когда мы стали глубже исследовать себя самих и мир вокруг нас. Наука - это одна из сменяющих друг друга систем веры, которыми мы пытается объяснять то, что наблюдаем, этим самым изменяя себя, чтобы приспособиться к новой информации, получаемой из внешнего мира. Многое из того, что мы видим и наблюдаем, можно объяснить единой теорией: теорией эволюции через наследственность, изменчивость и отбор.
Поэтому неудивительно, что ученые, занимающиеся компьютерными исследованиями, обратились к теории эволюции в поисках вдохновения. Возможность того, что вычислительная система, наделенная простыми механизмами изменчивости и отбора, могла бы функционировать по аналогии с законами эволюции в природных системах, была очень привлекательна. Эта надежда стала причиной появления ряда вычислительных систем, построенных на принципах естественного отбора.
Главная трудность с возможностью построения вычислительных систем, основанных на принципах естественного отбора и применением этих систем в прикладных задачах, состоит в том, что природные системы достаточно хаотичны, а все наши действия, фактически, носят четкую направленность. Мы используем компьютер как инструмент для решения определенных задач, которые мы сами и формулируем, и мы акцентируем внимание на максимально быстром выполнении при минимальных затратах. Природные системы не имеют никаких таких целей или ограничений, во всяком случае нам они не очевидны. Выживание в природе не направлено к некоторой фиксированной цели, вместо этого эволюция совершает шаг вперед в любом доступномее направлении.
Метод роящихся частиц
Это наиболее простой и, что удивительно, один из самых молодых методов эволюционного программирования, появившийся в середине 90-х годов. Группа исследователей, занимавшихся этологией птиц и рыб, их социальной организацией, пришла к выводу о возможности решения задач оптимизации с помощью моделирования поведения групп животных. В основу метода положен тот факт, что при формировании стаи птицы стремятся к некоторому центру “притяжения”, постепенно замедляя скорость полёта.
В реализации данного алгоритма многомерное пространство поиска населяется роем частиц (элементарных решений). Координаты частицы в пространстве однозначно определяют решение задачи оптимизации. Помимо координат каждая из частиц описывается скоростью перемещения и ускорением. В процессе перемещения частицы осуществляют “прочёсывание” пространства решений и тем самым находят текущий оптимум, к которому на следующем шаге устремляются остальные частицы. Для введения случайной составляющей в процесс поиска могут быть включены “сумасшедшие” частицы, закон движения которых отличается от закона движения остальных.
Схема работы алгоритма выглядит следующим образом.
- Создаётся исходная “случайная” популяция частиц.
- Для каждой частицы рассчитывается целевая функция.
- Лучшая частица с точки зрения целевой функции объявляется “центром притяжения”.
- Векторы скоростей всех частиц устремляются к этому “центру”, при этом чем дальше частица находится от него, тем большим ускорением она обладает.
- Осуществляется расчёт новых координат частиц в пространстве решений.
- Шаги 2—5 повторяются заданное число раз.
- Последний “центр тяжести” объявляется найденным оптимальным решением.
Этот алгоритм благодаря своей простоте (менее десяти строк кода) и скорости считается очень перспективным для задач планирования.
Одной из разновидности метода роящихся частиц является канонический метод роя частиц.
Рассмотрим задачу глобальной безусловной минимизации целевой функций 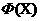 в в 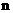 -мерном арифметическом пространстве -мерном арифметическом пространстве 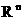 : :
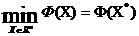 . (1) . (1)
Множество частиц обозначим 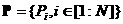 , где , где 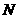 - количество частиц в рое (размер популяции). В момент времени - количество частиц в рое (размер популяции). В момент времени 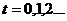 координаты частицы координаты частицы 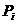 определяются вектором определяются вектором 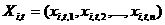 , а ее скорость - вектором , а ее скорость - вектором 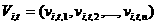 . Начальные координаты и скорости частицы . Начальные координаты и скорости частицы 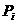 равны равны 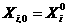 , , 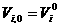 , соответственно. , соответственно.
Итерации в каноническом методе PSO выполняются по следующей схеме:
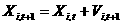 ; (2) ; (2)
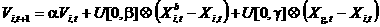 . (3) . (3)
Здесь 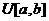 представляет собой представляет собой 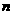 -мерный вектор псевдослучайных чисел, равномерно распределенных в интервале -мерный вектор псевдослучайных чисел, равномерно распределенных в интервале 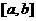 ; ;  - символ покомпонентного умножения векторов; - символ покомпонентного умножения векторов; 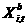 - вектор координат частицы - вектор координат частицы 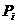 с наилучшим (в смысле (1)) значением целевой функции с наилучшим (в смысле (1)) значением целевой функции 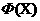 за все время поиска; за все время поиска; 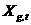 - вектор координат соседней с данной частицы с наилучшим за время поиска значением целевой функции - вектор координат соседней с данной частицы с наилучшим за время поиска значением целевой функции 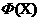 ; ; 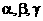 - свободные параметры алгоритма. - свободные параметры алгоритма.
Пересчет координат частиц по формулам (2), (3) может происходить по синхронной схеме (обновление координат частиц выполняется только после определения текущих скоростей всех 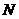 частиц) или по асинхронной схеме (расчет новых координат части производится до завершения указанных вычислений). частиц) или по асинхронной схеме (расчет новых координат части производится до завершения указанных вычислений).
В процессе итераций вектор 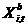 образует, так называемый, собственный путь (private guide) частицы образует, так называемый, собственный путь (private guide) частицы 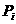 , а вектор , а вектор 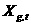 - локальный путь (local guide) этой частицы. - локальный путь (local guide) этой частицы.
Свободный параметр 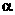 определяет «инерционные» свойства частиц (при определяет «инерционные» свойства частиц (при 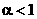 движение частиц, очевидно, замедляется). Рекомендуемое значение параметра движение частиц, очевидно, замедляется). Рекомендуемое значение параметра 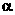 равно 0.7298. В процессе оптимизации может быть эффективным постепенное уменьшение коэффициента равно 0.7298. В процессе оптимизации может быть эффективным постепенное уменьшение коэффициента 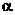 от 0.9 до 0.4. При этом большие значения параметра обеспечивают широкий обзор пространства поиска, а малые – точную локализацию минимума целевой функции. Рекомендуемые значения свободных параметров от 0.9 до 0.4. При этом большие значения параметра обеспечивают широкий обзор пространства поиска, а малые – точную локализацию минимума целевой функции. Рекомендуемые значения свободных параметров 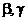 равны 1.49618. равны 1.49618.
Важнейшим понятием в методе PSO является понятие соседства частиц, которое определяется соответствующей топологией соседства.
Второй компонент в формуле (3) называется «когнитивным» компонентом (по социальной аналогии) и формализует тенденцию частицы вернуться в положение с минимальным значением целевой функции. Третий компонент в формуле (3) называется «социальным» компонентом. Компонент отражает влияние на данную частицу ее соседей.
Известны также методы, использующие несколько роев и миграцию частиц между ними. Идея многороевого метода с миграцией частиц состоит в формировании нескольких роев частиц и организации миграции частиц между роями. При этом каждый из роев использует, вообще говоря, свои значения свободных параметров и свою топологию соседства частиц.
Генетические алгоритмы
Генетические алгоритмы это алгоритмы, использующие методы "эволюционного вычисления". Эволюционное вычисление занимается решением проблем, используя приложения эволюционных механизмов. Эта область развилась из трех более или менее независимых разработок: генетических алгоритмов, эволюционного программирования и эволюционных стратегий. Весь три дисциплины начали изучаться в 60-х годах и 70-х годах (первые две в США, третья в Германии), но только в конце 80-х годов они начали признаваться. В настоящее время генетические алгоритмы рассматриваются как одни из наиболее успешных методов машинного обучения. По существу, они являются процедурами оптимизации, имитирующими при проектировании модели данных такие процессы, как генетическая рекомбинация, мутация и отбор, аналогичные тем, что обусловливают естественную эволюцию. Первые генетические алгоритмы были предложены в начале 70-х годов Джоном Холландом (John Holland) с целью имитации эволюционных процессов в живой природе.
Генетические алгоритмы - адаптивные методы поиска, которые в последнее время часто используются для решения задач функциональной оптимизации. Они основаны на генетических процессах биологических организмов: биологические популяции развиваются в течении нескольких поколений, подчиняясь законам естественного отбора и по принципу "выживает наиболее приспособленный" (survival of the fittest).
Схему конструирования генетического алгоритма для решения задач можно представить следующим образом:
- разработайте хорошее кодирование задачи в терминах строк ограниченного алфавита;
- постройте искусственную среду в компьютере, где решения могут конкурировать друг с другом. Обеспечьте объективную оценку успеха или неудачи, что в профессиональных терминах называется функцией пригодности;
- разработайте способы, которыми возможные решения могут быть объединены. Здесь очень популярна так называемая операция скрещивания (кроссинговер), в который строки отца и матери просто отрезаются и после выделения отрезанные части объединяются вместе. При репродукции могут быть применены другие операторы, такие как операторы мутации, инверсии и т.д.;
- введите хорошо изменяемую начальную популяцию и заставьте компьютер играть в "эволюцию", удаляя плохие решения из каждого поколения и заменяя их потомством или мутациями хороших решений;
- остановитесь, когда будет порождено семейство успешных решений.
Схема достаточна проста, но успех будет зависеть, прежде всего, от адекватного задаче кодирования (так называемая техника представления) и нахождения эффективных операторов мутации.
Удачи и недостатки генетических алгоритмов частично сходны с таковыми при естественном отборе вообще. Двумя недостатками являются большое перепроизводство объектов и случайный характер процесса поиска. В общем случае требуется масса вычислительной мощности, чтобы достигнуть чего-нибудь значительного. С другой стороны, методика устойчива; если решение существует, то генетический алгоритм с большой вероятностью найдет его. Однако, в специфической проблемной области исследования операций, генетические алгоритмы часто не согласовываются с общепринятыми алгоритмами, их работоспособность главным образом является следствием их широкой применимости и концептуальной ясности. Вместе со своими родственниками, нейронными сетями, они являются ядром самообучающихся систем.
Схема работы генетических алгоритмов выглядит следующим образом.
- Задается способ кодирования параметров задачи в “хромосомах”.
- Создается исходная популяция (начальное решение).
- Рассчитывается функция приспособленности каждой особи.
- Для наиболее приспособленных особей производится “скрещивание” и рождение новых особей, содержащих признаки обоих родителей. При этом передача признаков осуществляется в соответствии с одним из выбранных способов “обмена участков хромосом”. Наименее приспособленные особи “отмирают” и заменяются новорожденными.
- Осуществляется мутация некоторой части особей добавлением в процесс поиска элемента случайности.
- Шаги 2—5 итерационно повторяются заданное число раз.
- Из оставшейся популяции выбираются лучшие особи, “хромосомы” декодируются, а получаемое таким образом решение соответствует локальному оптимуму.
Генетические алгоритмы в различных формах применились ко многим научным и техническим проблемам. Генетические алгоритмы использовались при создании других вычислительных структур, например, автоматов или сетей сортировки. В машинном обучении они использовались при проектировании нейронных сетей или управлении роботами. Они также применялись при моделировании развития в различных предметных областях, включая биологические (экология, иммунология и популяционная генетика), социальный (такие как экономика и политические системы) и когнитивные системы.
Тем не менее, возможно наиболее популярное приложение генетических алгоритмов - оптимизация многопараметрических функций. Многие реальные задачи могут быть сформулированы как поиск оптимального значения, где значение - сложная функция, зависящая от некоторых входных параметров. В некоторых случаях, представляет интерес найти те значения параметров, при которых достигается наилучшее точное значение функции. В других случаях, точный оптимум не требуется - решением может считаться любое значение, которое лучше некоторой заданное величины. В этом случае, генетические алгоритмы - часто наиболее приемлемый метод для поиска "хороших" значений. Сила генетического алгоритма заключена в его способности манипулировать одновременно многими параметрами, эта особенность ГА использовалось в сотнях прикладных программ, включая проектирование самолетов, настройку параметров алгоритмов и поиску устойчивых состояний систем нелинейных дифференциальных уравнений.
Структура данных генетического алгоритма состоит из одной или большее количество хромосом (обычно из одной). Как правило, хромосома - это битовая строка, так что термин строка часто заменяет понятие "хромосома". В принципе, ГА не ограничены бинарным представление. Известны другие реализации, построенные исключительно на векторах вещественных чисел
Каждая хромосома (строка) представляет собой конкатенацию ряда подкомпонентов называемых генами. Гены располагаются в различных позициях или локусах хромосомы, и принимают значения, называемые аллелями. В представлениях с бинарными строками, ген - бит, локус - его позиция в строке, и аллель - его значение (0 или 1).
Табуированный поиск (Tabu Search)
Данная процедура представляет собой вариацию известного метода градиентного спуска с памятью. В процессе поиска ведётся список табуированных (запрещённых для перехода) позиций (из числа уже посещённых и рассчитанных). Критические параметры алгоритма — глубина списка запретов, определение текущего состояния, размер области вокруг текущего состояния. В процессе поиска осуществляются операции аспирации (включение в запрещённый список состояний вокруг текущего состояния) и диверсификации, которая добавляет фактор случайности в процесс поиска.
Моделирование отжига (Simulated Annealing).
Метод, разработанный в 80-х годах, основан на аналогии с физическим процессом охлаждения металла и переходом его в состояние с минимальной энергией кристаллической решётки. Изначально он использовался для моделирования поведения системы атомов при разных температурах, но впоследствии был расширен для решения комбинаторных задач.
Схема применения метода достаточно проста.
- Задается начальное условие.
- Выбираются соседние состояния и определяется вероятность перехода в каждое из этих состояний, которая зависит от их “энергии”.
- Уменьшается температура (от нее зависит вероятность перехода в новое состояние).
- Шаги 2—3 повторяются заданное число раз.
Муравьиные алгоритмы
Каждый, кто хоть раз в жизни наблюдал за муравьями, обязательно должен был заметить: вся деятельность этих насекомых имеет ярко выраженную групповую окраску. Работая вместе, группа муравьев способна затащить в муравейник кусок пищи или строительного материала, в 10 раз больше самих работников. Ученые давно знают об этом, но только в последнее время задумались о полезном применении муравьиного опыта в повседневной жизни.
Например, группа муравьев прекрасно умеет находить кратчайшую дорогу к пище. Если какое-нибудь препятствие - палка, камень, нога человека - встает на пути, бравые добытчики быстро находят новый оптимальный маршрут.
Муравьи решают проблемы поиска путей с помощью химической регуляции. Каждый муравей оставляет за собой на земле дорожку особых веществ - феромонов. Другой муравей, почуяв след на земле, устремляется по нему. Чем больше по одному пути прошло муравьев - тем явнее след, а чем явнее след - тем большее «желание» пойти в ту же сторону возникает у муравьев. Поскольку муравьи, нашедшие самый короткий путь к «кормушке», тратят меньше времени на путь туда и обратно, их след быстро становится самым заметным. Он привлекает большее число муравьев, и круг замыкается. Остальные пути - менее используемые - потихоньку пропадают.
Алгоритмы муравья, или оптимизация по принципу муравьиной колонии (это название было придумано изобретателем алгоритма, Марко Дориго), основаны на применении нескольких агентов и обладают специфическими свойствами, присущими муравьям, и используют их для ориентации в физическом пространстве. Алгоритмы муравья особенно интересны потому, что их можно использовать для решения не только статичных, но и динамических проблем, например, в изменяющихся сетях.
|