Практическая работа №4.
«Аппроксимация функций с помощью нейронных сетей»
Тема 5 «Нейронные сети»
Цель: изучение принципов обучения и функционирования многослойных сетей
Теория:
Структура нейрона представлена на рисунке 1. Внутри нейрона можно
выделить блок суммирования, определяющий взвешенную сумму всех входных
сигналов
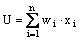
и блок функции активации Y = F(U). Таким образом, нейрон функционирует
за два такта: 1) суммирование входных сигналов и 2) вычисление Y по
функции активации.
Функция активации должна удовлетворять двум условиям: 1)
|F(U)| < 1 при любом U, 2) функция должна быть монотонной
неубывающей.
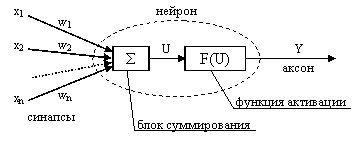
Рисунок 1 – Структура нейрона
Нейронная сеть (НС) представляет собой совокупность нейронов, связанных между собой соответствующим образом.
Нейроны образуют нейронные сети путем соединения синапсов с аксонами.
Наиболее распространенными и хорошо изученными являются трехслойные НС,
состоящие из трех слоев нейронов: входного, скрытого и выходного
(рисунок 2). Нейроны входного слоя имеют только по одному синапсу.
Количество нейронов входного слоя соответствует количеству входных
переменных сети Х. Задачей нейронов этого слоя является только
распределение входных сигналов по нейронам скрытого слоя, суммирования
и вычисления функции активации в них не происходит. Количество нейронов
в скрытом слое может быть различным и часто подбирается
экспериментально. Недостаточное или избыточное количество нейронов в
скрытом слое приводит к ухудшению точности аппроксимации. Кроме того,
избыточное количество усложняет сеть и уменьшает быстродействие.
Нейроны выходного слоя формируют выходные сигналы, их количество
соответствует количеству выходов Y. Пример НС с 3 входными, 4 скрытыми
и 2 выходными нейронами приведен на рисунке 2. Такая НС для краткости
обозначается как (3-4-2). Нij – нейроны.
Данные сети относятся к сетям прямого распространения, поскольку в них
входные сигналы последовательно проходят через все нейроны и после
преобразований напрямую подаются на выходы. Выходной сигнал yij каждого
j-го нейрона в i-м слое определяется как
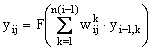 , ,
где n(i) – число нейронов в i-м слое.

Рисунок 2 – Нейронная сеть вида (3-4-2)
Наиболее
популярный класс многослойных сетей прямого распространения образуют
многослойные персептроны (MLP), в которых каждый вычислительный элемент
использует пороговую или сигмоидальную функцию активации. Многослойный
перцептрон может формировать сколь угодно сложные границы принятия
решения и реализовывать произвольные булевы функции.
Аппроксимация функций с помощью нейронных сетей
Нейронные сети относятся к классу аппроксиматоров и «черных
ящиков», аппроксимирующих некоторые функции вида Y = F(X), где Y
– вектор выходных переменных, Х – вектор входных.
Процесс аппроксимации заключается в подборе весовых коэффициентов wij и
называется обучением НС. То есть НС может функционировать в двух
режимах:
- эксплуатации, когда на вход подаются сигналы, а на выходе снимаются результаты вычислений;
- обучения, когда происходит корректировка весов таким образом, чтобы
выходные сигналы наиболее точно соответствовали желаемым.
От качества обучения НС зависит точность ее работы в режиме эксплуатации.
Структура процесса обучения представлена на рисунке3, где обозначены:
Yжел – желаемые значения выходных сигналов, Е – ошибка
обучения (Е = Yжел – Y), К – корректирующие воздействия
(обычно изменения весов Dwij).

Рисунок 3– Процесс обучения НС
Для обучения НС составляется обучающая выборка входных сигналов и
соответствующих им выходных. Выборка может быть разделена на две части:
рабочую выборку (на основе которой производится собственно обучение) и
тестирующую выборку (для проверки качества обучения).
Весам
синапсов необученной НС изначально присваиваются произвольные значения.
Далее на вход НС подается первый вектор Х из рабочей выборки,
определяется вектор Y и ошибка обучения Е. Исходя из значений вектора Е
корректируются веса синапсов. Затем подается следующий вектор Х из
выборки и т.д. Циклы обучения повторяются многократно, пока качество
обучения не станет удовлетворительным (это можно проверить по
тестирующей выборке).
Для обучения обычно используется НС с функциями активации сигмоидного типа:
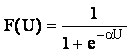 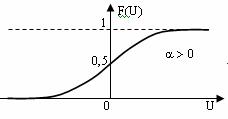
Целью обучения по правилу обратного распространения является минимизация ошибки обучения.
Задание:
- Выполнить ручной просчет для аппроксимации функции (заданной согласно варианту) с помощью НС на рис. 3.
Пример:
Выполнить аппроксимацию функции с помощью НС: y = x1 + x2,
x1, x2Є[1, 10], где Х – вектор входных переменных Х = {х1,
х2, …}, Y – вектор выходных переменных.
Так
как функция имеет один выходной сигнал (y), то выходной слой НС будет
состоять из одного нейрона, а также два входных сигнала (x1, x2), т.е.
входной слой будет состоять из двух нейронов.
В итоге получаем нейронную сеть следующей структуры (рис. 3)
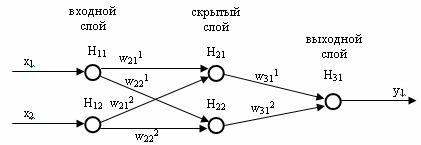
Рисунок 3 – Пример нейронной сети
В качестве функции активации будет использоваться сигмоидная с коэффициентом a = 1:
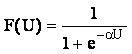 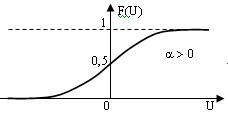
Начальные значения весов синаптических связей принимаются равными 0,5:
w211 = w221 = w212 = w222 = w311 = w312 = 0,5.
Скорость обучения принимается равной n = 0,2.
Строим обучающую выборку из пяти значений:
Х1
Х2
Y
0
1
1
2
0
2
3
1
4
1
1
2
4
2
6
Выполним нормировку обучающей выборки (поделив Х1 на 4, Х2 на 2, Y на 6):
Х1
Х2
Y
0
0,5
0,17
0,5
0
0,33
0,75
0,5
0,67
0,25
0,5
0,33
1
1
1
Далее выполняем обучение:
Шаг 1: На входы НС подается первый вектор входных параметров: х1 = 0 и х2 = 0,5. При этом ужел = 0,17.
Выходы нейронов входного слоя: Y11 = 0, Y12 = 0,5.
Для скрытого слоя:
U21 = w211*Y11 + w212*Y12 = 0,5*0 + 0,5*0,5 = 0,25;
U22 = w221*Y11 + w222*Y12 = 0,5*0 + 0,5*0,5 = 0,25;
Y21 = 1 / (1 + exp(-a*U21)) = 1 / (1 + exp(-0,25)) = 0,562;
Y22 = 1 / (1 + exp(-a*U22)) = 1 / (1 + exp(-0,25)) = 0,562.
Для выходного слоя:
U31 = w311*Y21 + w312*Y22 = 0,5*0,562 + 0,5*0,562 = 0,562;
Y31 = 1 / (1 + exp(-a*U31)) = 1 / (1 + exp(-0,562)) = 0,636.
Получили
выходное значение (0,636) не совпадающее с желаемым 0,17 поэтому
вычисляем величину градиента выходного и скрытого слоев.
Шаг 2: Величина градиента для выходного нейрона:
EI31 = (Y31 – yжел)*Y31*(1 – Y31) = (0,636 –
0,17)*0,636*(1 - 0,636) = 0,078.
Шаг 3. Величины градиентов для скрытого слоя:
EI21 = Y21*(1 – Y21)*[EI31*w311] = 0,562*(1 – 0,562)*0,078*0,5 = 0,0096,
EI22 = Y22*(1 – Y22)*[EI31*w312] = 0,562*(1 – 0,562)*0,078*0,5 = 0,0096.
Шаг 4. Коррекция весов синапсов:
w211 = w211 - n*Y11*EI21 = 0,5 – 0,2*0*0,0096 = 0,5
w221 = w221 - n*Y11*EI22 = 0,5 – 0,2*0*0,0096 = 0,5
w212 = w212 - n*Y12*EI21 = 0,5 – 0,2*0,5*0,0096 = 0,499
w222 = w222 - n*Y12*EI22 = 0,5 – 0,2*0,5*0,0096 = 0,499
w311 = w311 - n*Y21*EI31 = 0,5 – 0,2*0,562*0,078 = 0,491
w312 = w312 - n*Y22*EI31 = 0,5 – 0,2*0,562*0,078 = 0,491.
Шаг 5. Обнуляем все значения на НС, кроме весов синапсов. Повторяем шаг 1, только используя измененные веса синапсов.
Выходы нейронов входного слоя: Y11 = 0, Y12 = 0,5.
Для скрытого слоя:
U21 = w211*Y11 + w212*Y12 = 0,5*0 + 0,499*0,5 = 0,2495;
U22 = w221*Y11 + w222*Y12 = 0,5*0 + 0,499*0,5 = 0,2495;
Y21 = 1 / (1 + exp(-a*U21)) = 1 / (1 + exp(-0,2495)) = 0,562;
Y22 = 1 / (1 + exp(-a*U22)) = 1 / (1 + exp(-0,2495)) = 0,562.
Для выходного слоя:
U31 = w311*Y21 + w312*Y22 = 0,491*0,562 + 0,491*0,562 = 0,552;
Y31 = 1 / (1 + exp(-a*U31)) = 1 / (1 + exp(-0,552)) = 0,634.
Полученное
значение уже ближе к желаемому ужел = 0,17. То есть данный цикл
обучения приблизил ответ НС к желаемому на величину Dу = 0,636 –
0,634 = 0,002.
Шаг 6.
На вход нейронной сети подается второй вектор входных параметров:
х1 = 0,5 и х2 = 0. При этом ужел = 0,33. Повторяем шаги с 1 по 5,
используя измененные значения весов.
Выходы нейронов входного слоя: Y11 = 0,5, Y12 = 0.
- В блокноте создать текстовый файл и сохранить в нем обучающую выборку (не нормированную), дополнив ее еще 5 значениями.
- Придумать 2 тестовых примера, т.е. взять два набора входных значений и вручную просчитать значения функции.
- Запустить программу Neural Network Wizard
- В первом окне указать файл с обучающей выборкой и нажать кнопку Далее.
- В
новом окне перечислен список доступных полей, взятый из первой строки
указанного файла. Для каждого из полей необходимо указать, чем является
данная переменная. Если данная переменная входная, то в группе
«Использовать поле как» выбирается вариант
«Входное», если выходная – «Целевое».
Кроме того, для каждой переменной можно указать вид нормализации
(приведения к диапазону [0,1]) с соответствующими параметрами. Кнопка
«Далее» переводит к следующему окну.
- Определяется
структура и параметры НС: количество скрытых слоев, количество нейронов
в каждом слое, а также вид сигмоидной функции.
- Задаются
параметры обучения и критерии остановки обучения, если она требуется
(установить параметры «Использовать для обучения
нейросети»-90%, «Скорость обучения» - 0,2,
«Критерий остановки обучения» - прошло 50000 эпох). Кнопка
«Далее» показывает краткий предварительный отчет.
- В
следующем окне визуализирован процесс обучения. Чтобы запустить
обучение, нажимается кнопка «Пуск обучения». На верхней
диаграмме показано распределение ошибки обучения: по горизонтали
значение ошибки (чем правее столбец, тем больше ошибка), по вертикали
количество примеров из выборки с данной ошибкой. Зеленые столбцы
– ошибка на рабочей обучающей выборке, красные – на
тестовой. В процессе обучения столбцы должны стремиться в левую часть
диаграммы. Ниже диаграммы отображается распределение примеров на
рабочей и тестовой выборках. Каждый пример изображен здесь точкой. Чем
ближе точка к диагонали, тем точнее НС предсказала ее значение.
Остановка обучения происходит либо по ранее указанному критерию, либо с помощью той же кнопки «Пуск обучения».
Провести обучение, затем нажать кнопку Далее.
- В
следующем окне представляется возможность оценить точность работы НС в
эксплуатационном режиме. Для этого используются тестовые примеры.
Введите сначала набор входных значений первого тестового примера и
нажмите кнопку Расчет. Сравните полученное значение с тем, что у Вас
получилось при ручном вычислении значения функции. Введите второй
тестовый пример.
- Вернуться
к окну с настройками параметрами сети и увеличить (примерно в два раза)
количество нейронов в скрытом слое. Снова обучить сеть, провести
тестовые примеры и посмотреть, как изменился результат.
- Вернуться
к окну с настройками параметрами сети и увеличить (примерно в два раза)
количество скрытых слоев. Снова обучить сеть, провести тестовые примеры
и посмотреть, как изменился результат.
- Закрыть программу.
Отчет:
Отчет должен включать следующие разделы:
- Подробное описание ручного просчета для аппроксимации функции c зарисованной структурой нейронной сети
- Содержимое текстового файла с обучающей выборкой
- Два тестовых примера
- Результаты
работы программы после первого запуска. Рассчитать погрешность
полученных результатов от желаемых в тестовых примерах.
- Результаты
работы программы после второго запуска. Рассчитать погрешность
полученных результатов от желаемых в тестовых примерах, и погрешность
полученных результатов в первом запуске от второго.
- Результаты
работы программы после третьего запуска. Рассчитать погрешность
полученных результатов от желаемых в тестовых примерах, и погрешность
полученных результатов в первом запуске от второго и погрешность - во
втором запуске от третьего.
- Сделать вывод, когда были получены лучшие результаты.
Варианты заданий:
Соответствует номеру в списке
Вариант |
Задание |
1 |
y = 2*sin2x, х I[0, 1] |
2 |
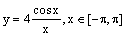
|
3 |
y1 = 0.5*x2 – 4.8*x + 3.5, y2 = x3 – 12, y3 = x + 3,5, x I [1, 10] |
4 |
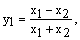 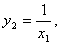 x1, x2 I [1, 10] x1, x2 I [1, 10]
|
5 |
y1 =x1 – x2, y2 = x1 + x2, y3 = x1*x2; x1, x2 I [1, 10] |
6 |
y1 = x1*sin(x2), y2 = x1*cos(x2); x1 I [1, 10], x2 I [-90°, +90°] |
7 |
y1 = x1*x2 + x3, y2 = 2*y1; x1, x2, x3 I [1, 10] |
8 |
y1 = 1,5*x1 + (x2 – 2*x3), y2 = x3 – y1; x1, x2, x3 I [1, 10] |
9 |
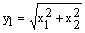 , , 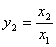 ; x1, x2 I [-10, 10] ; x1, x2 I [-10, 10]
|
10 |
y1 = 2,3*x1*x2 – 0,5*x12 + 1,8*x2, y2 = y12; x1, x2 I [1, 10] |
11 |
y = 2*x1 + 5*x1*x2 + x2; x1, x2 I [-5, 5] |
12 |
y = sin x1*sin x2*sin x3 ; x1, x2, x3 I [0, p] |
13 |
y = 2*x1*cos x2, x1 I [0,1], x2 I [0, p] |
14 |
y = x1 + x2 + x3, xi I [0, 10] |
15 |
y = x1*х1 + x2* x2 + x3*x3, xi I [0, 10] |
16 |
y = 2x1 + 3x2 + 4x3, xi I [0, 10] |
17 |
y = 5(x1 + x2) – x3, xi I [0, 10] |
18 |
y = x1 + x2 - x3, xi I [0, 10] |
19 |
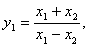 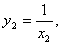 x1, x2 I [1, 10] x1, x2 I [1, 10]
|
20 |
y1 =x1 – x2, y2 = x1 + x2, y3 = x1*x2; x1, x2 I [1, 10] |
|