4.1. Модели контроля
Реальные сложные системы можно исследовать с помощью двух типов математических моделей: аналитических и имитационных. В аналитических моделях поведение сложных систем записывается в виде некоторых функциональных соотношений или логических условий. Наиболее полное исследование удается провести в том случае, когда получены явные зависимости, связывающие искомые величины с параметрами сложной системы и начальными условиями ее изучения. Однако аналитическое исследование удается выполнить только для сравнительно простых систем.
Термин "имитационное моделирование" означает, что мы имеем дело с такими математическими моделями, с помощью которых результат нельзя заранее вычислить или предсказать, поэтому для прогноза поведения реальной сложной системы необходим эксперимент (имитация) на модели при заданных исходных данных. Имитация представляет собой численный метод проведения на ЭВМ экспериментов с математическими моделями, описывающими поведение сложной системы в течение заданного или формируемого периода времени. Поведение компонентов сложной системы и их взаимодействие в имитационной модели чаще всего описываются набором алгоритмов, реализуемых на некотором языке моделирования. Имитируя различные реальные ситуации на имитационной модели, исследователь получает возможность решения таких задач, как оценка эффективности различных принципов управления системой, сравнение вариантов структуры системы, определение степени влияния изменений параметров системы и начальных условий имитации ее поведения на показатель эффективности системы.
Совместная работа циклов контроля и управления придает управляемому процессу динамические свойства [17]. С помощью моделей цикла контроля постоянно анализируется фактическое протекание управляемого процесса в ГАП, прогнозируется ожидаемый характер развития управляемого процесса и определяется фактическая и прогнозируемая степень достижения поставленных целей. При этом в цикле контроля решаются следующие основные задачи [17];
- по имеющимся данным производится оценка параметров состояния П1, П2 ... , характеризующих положение управляемых объектов ГАП, проверка выполнения событий С1, С2, ... , предусмотренных решениями, оценка значений параметров К1, К2, ... , характеризующих поставленную цель, например, поддержание контролируемого параметра X в заданных пределах от К1 до К2 Оценки вычисляются как для текущих значений параметров П, К и X, так и для прогнозируемых на заданный момент в будущем;
- по полученным значениям параметров и вероятностей событий определяются функции, позволяющие оценить степень достижения поставленных целей и выполнения принятых решений, т.е. функции качества управления ω;
- вырабатываются значения диалогового сигнала тревоги L.
Если цель выполняется в должной степени, то значение L принимается равным нулю. Если контролируемый параметр X недопустимо отклоняется от заданных значений К1 или К2, вырабатывается сигнал L=1. Для УКВ - это сигнал тревоги, указание на необходимость внесения коррекции в технологический процесс. Далее выполняется цикл управления, в котором корректируются решения, новые решения ставятся на контроль и орган управления ГАП начинает функционировать в цикле контроля. Структура процесса контроля решений представлена на рис. 29.
Следует отметить, что анализ фактического состояния не требует вычисления функции ω. Значение диалогового сигнала L здесь вычисляется непосредственно по факту осуществления события:
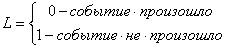
Поэтому контроль по прогнозируемым событиям идентичен контролю по параметрам, в связи с чем далее рассматриваются преимущественно методы контроля по параметрам [10].
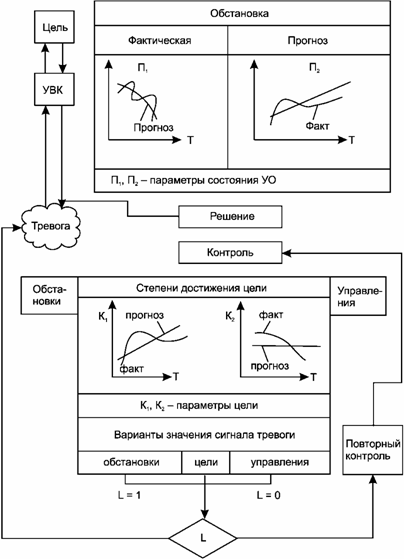
Рис. 29. Структура процесса контроля решений
Рассмотрим случай, когда контроль за ходом управляемого процесса ведется по фактическим значениям детерминированного параметра X. Можно считать, что управляемый процесс протекает в соответствии с заданной целью, если для параметра X, фактически характеризующего процесс, выполняется условие 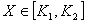 . В этом случае ω= 1. Если фактическое значение параметра состояния меньше нижней границы К1 требуемого диапазона, т.е. X <К1 то управляемый процесс протекает хуже, чем требуется. Степень ухудшения можно оценить по значению
. В этом случае ω= 1. Если фактическое значение параметра состояния меньше нижней границы К1 требуемого диапазона, т.е. X <К1 то управляемый процесс протекает хуже, чем требуется. Степень ухудшения можно оценить по значению
ω= 1-(К1-Х)/К1=Х/К1
Аналогично, если выполняется условие X > К2.
ω=1 + (Х-К2)/К2=Х/К2
Объединяя эти соотношения, получим для функции качества управления следующие выражения:
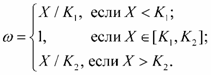 (36)
(36)
Тогда в соответствии с этим выражением очевидно соотношение:
ω = Y(X, K1, K2) (37)
Выбор для вычисления ω простейшей функции Y определяется наглядностью получаемых результатов. В самом деле, использование Y позволяет не только установить факт попадания или непопадания параметра X в заданный интервал значений [K1, K2], но и определить степень отклонения X от границ K1 и K2 при выходе X за его пределы. В этом смысле качество управления ω = Y аналогично вероятности выполнения поставленной задачи.
Следует отметить, что в силу неконтролируемых случайных воздействий нижняя K1 и верхняя K2 границы требуемого диапазона могут смещаться случайным образом. Поэтому, наряду с требуемым диапазоном необходимо рассматривать также допустимый диапазон 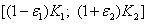 . При нахождении параметра X в допустимом диапазоне качество управления снижается, но не настолько, чтобы вырабатывался сигнал "тревога". Иначе говоря, в этом диапазоне формируется сигнал управления (подналадки). И лишь при выходе значения X за пределы допустимого диапазона должен быть выработан сигнал L=1 ("тревога", управление, подналадка, стоп и т.д.).
. При нахождении параметра X в допустимом диапазоне качество управления снижается, но не настолько, чтобы вырабатывался сигнал "тревога". Иначе говоря, в этом диапазоне формируется сигнал управления (подналадки). И лишь при выходе значения X за пределы допустимого диапазона должен быть выработан сигнал L=1 ("тревога", управление, подналадка, стоп и т.д.).
Схема формирования диалоговых сигналов, характеризующих состояние управляемого процесса, показана на рис. 30. Как уже отмечалось, сигнал "тревога" L=1 вырабатывается при выходе параметра состояния X за пределы допустимого диапазона 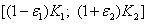 . При принятом способе вычисления качества управления это эквивалентно непопаданию ω в интервал
. При принятом способе вычисления качества управления это эквивалентно непопаданию ω в интервал 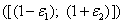 , где
, где 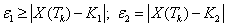 . В этих выражениях Х(Тk ) – значения параметров, вырабатываемые управляемой системой в конце цикла обработки. Желаемый диапазон [K1, K2] в соответствии с характером процесса может стягиваться в точку. При этом К1=К2 и малейшее смещение параметров состояния Х в сторону больших или меньших , чем заданный диапазон значений приводило бы при e1=e2=0 к выработке сигнала «тревога» и, следовательно, к необходимости коррекции первоначального состояния системы. Поскольку точное совпадение Х с заданным диапазоном маловероятно, орган управления ГАП при таком подходе исправно пребывал бы в состоянии «тревога» (пульсирующая подналадка, пульсирующая коррекция). Введение отличных от нуля величин e1 и e2 повышает устойчивость управления. Другими словами с помощью величин e1 и e2 можно регулировать скорость реакции органа управления на изменение в обстановке, тем меньше должны быть e1 и e2. И, наоборот, снижение точности данных об обстановке требует увеличения допустимых диапазонов изменения параметров состояния, т.е. увеличения значения e1 и e2.
. В этих выражениях Х(Тk ) – значения параметров, вырабатываемые управляемой системой в конце цикла обработки. Желаемый диапазон [K1, K2] в соответствии с характером процесса может стягиваться в точку. При этом К1=К2 и малейшее смещение параметров состояния Х в сторону больших или меньших , чем заданный диапазон значений приводило бы при e1=e2=0 к выработке сигнала «тревога» и, следовательно, к необходимости коррекции первоначального состояния системы. Поскольку точное совпадение Х с заданным диапазоном маловероятно, орган управления ГАП при таком подходе исправно пребывал бы в состоянии «тревога» (пульсирующая подналадка, пульсирующая коррекция). Введение отличных от нуля величин e1 и e2 повышает устойчивость управления. Другими словами с помощью величин e1 и e2 можно регулировать скорость реакции органа управления на изменение в обстановке, тем меньше должны быть e1 и e2. И, наоборот, снижение точности данных об обстановке требует увеличения допустимых диапазонов изменения параметров состояния, т.е. увеличения значения e1 и e2.
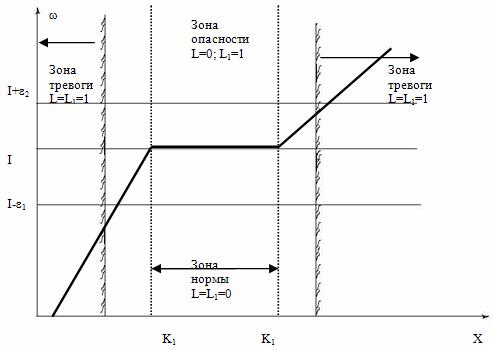
Рис.30. Схема формирования диалоговых сигналов
Таким образом. Приходим к следующему выражению для определения значений диалогового сигнала L:
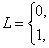 если
если 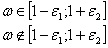 (38)
(38)
Область значения параметра состояния Х, в которой L=1 назовем зоной тревоги. Помимо ее имеет смысл рассматривать еще две зоны:
-зону опасности, в которой значение качества управления еще не вышло за пределы диапазона 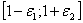 , но уже меньше или больше единицы. В этой зоне формируется сигнал «опасность», диалоговое значение которого может быть определено следующим образом:
, но уже меньше или больше единицы. В этой зоне формируется сигнал «опасность», диалоговое значение которого может быть определено следующим образом:
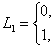 если
если 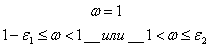
где L1- значение сигнала «опасность»,
-зону нормы, в которой качество управления принимает значение равное единице.
Ясно, что в зоне нормы оба диалоговых сигнала равны нулю. Можно считать, что в зоне нормы управляемый процесс протекает в соответствии с планом и в корректировке (подналадке) не нуждается. В зоне опасности корректировка процесса является еще преждевременной, но сигнал L=1 должен служить для органа управления признаком возможности перехода через некоторое время в зону тревоги. Наконец, при попадании в зону тревоги необходима корректировка (подналадка, поднастройка) управляемого процесса обработки.
Рассмотрим общую модель контроля по оцениваемым или прогнозируемым значениям недетерминированного параметра состояния (17).
Управляемые процессы, как правило, являются случайными, поэтому для описания и прогноза их протекания необходимо пользоваться вероятностными характеристиками. Исчерпывающей среди вероятностных характеристик является плотность f(х) или F(х) функции распределения случайных величины Х. Определив функцию f(х) или F(х), можно найти такие важные характеристики процесса, как вероятность того, что поставленная задача будет выполнена в заданном объеме (Р1) или в объеме не меньшем
Заданного (РII), или вероятность того, что цель не будет достигнута (РIII):
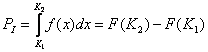
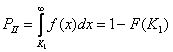
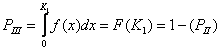
Вероятностные характеристики РI, РII и им подобные информативны сами по себе не могут использоваться и для вычисления функции w. Для того, это стало возможным, необходимо задать границы диапазона Р1 и Р2, за пределы которого не должна выходить вероятность решения поставленной задачи. Тогда, используя в качестве основной вероятностной характеристики величину, например РII, для функции w получаем соотношение, аналогичное:
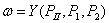 (39)
(39)
Значение величин Р1 и Р2 обычно не составляет труда; представление о порядке этих величин дают часть используемые значения: Р1=0,75¸0,80; Р2 =0,85¸0,90.
Однако метрологически такой подход для контроля по параметрам имеет недостатки, связанные с тем, что необоснованно увеличивается степень субъективности модели, поскольку УВК наряду с параметрами К1 и К2 должен дополнительно задавать значения Р1 и Р2, чем фактически меняет модель определения качества управления w. Поэтому следует искать пути обобщения модели (39) на рассматриваемый более общий случай.
Наиболее простым является использование оцениваемых или прогнозируемых значений математического ожидания 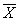 параметра Х. Для многих ситуаций этот путь может оказаться единственным, если значение
параметра Х. Для многих ситуаций этот путь может оказаться единственным, если значение 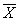 поддается оценке, а F(Х) –плотность распределения – известна. В этом случае для определения качества управления можно использовать ранее полученные соотношения (37), заменив во всех формулах Х и
поддается оценке, а F(Х) –плотность распределения – известна. В этом случае для определения качества управления можно использовать ранее полученные соотношения (37), заменив во всех формулах Х и 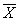 . Если кроме математического ожидания
. Если кроме математического ожидания 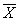 известна еще и дисперсия или среднеквадратическое отклонение s, то можно получить полные и достоверные оценки качества управления w. Зная плотность распределения параметров состояния f(Х), можно найти плотность распределения g(w) качества управления w, представляющего собой функцию случайного аргумента Х:
известна еще и дисперсия или среднеквадратическое отклонение s, то можно получить полные и достоверные оценки качества управления w. Зная плотность распределения параметров состояния f(Х), можно найти плотность распределения g(w) качества управления w, представляющего собой функцию случайного аргумента Х:
 если
если 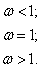
Как видно, w – смещенная (дискретно-непрерывная) случайная величина, поэтому плотность распределения g(w) в точке w=1 терпит разрыв. Соответственно имеет разрыв и закон распределения G(w) качества управления. Если обозначить через F(х) закон распределения параметра состояния Х, а закон F(ч) известен, поскольку известна плотность f(Х), то закон G(w) связан с F(х) следующим образом:
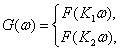 при
при 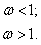
Плотность и закон распределения функции качества управления представлены на рис. 31 и 32 соответственно.
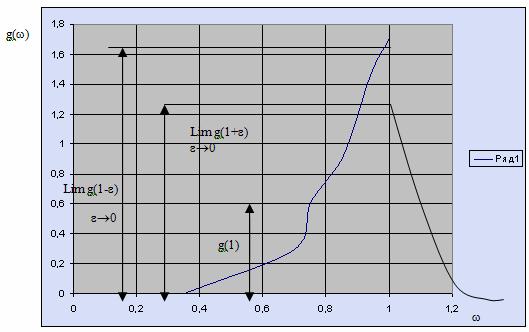
Рис 31. Плотность распределения функции качества управления w
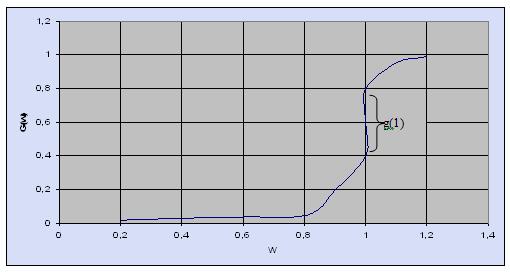
Рис 32. Закон распределения функции качества управления w
Для формирования диалоговых сигналов L и L1 необходимы значения математического ожидания 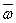 и дисперсии Dw или среднеквадратического отклонения
и дисперсии Dw или среднеквадратического отклонения 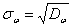 качества управления w.
качества управления w.
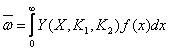 (40)
(40)
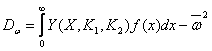 (41)
(41)
Если f – плотность нормального распределения, то формулы (40) и (41) преобразуются к виду:
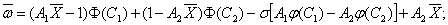 (42)
(42)
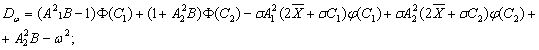 (43)
(43)
где 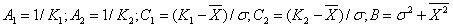
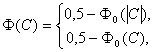 если
если 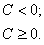
Функции 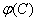 и
и 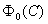 подробно табулированы, имеют стандартные программы для их определения, поэтому вычисления по формулам (42) и (43) не представляют труда.
подробно табулированы, имеют стандартные программы для их определения, поэтому вычисления по формулам (42) и (43) не представляют труда.
Таким образом, для недетерменированных параметров состояния выработка диалогового сигнала тревоги L ведется путем анализа попадания или непопадания значения математического ожидания качества управления 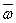 в интервал
в интервал 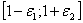 .
.
Сложнее обстоит дело с формированием сигнала опасности L1. Точечный прогноз 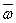 является в данном случае недостаточным, необходим интервальный прогноз, т.е. отыскание такого диапазона
является в данном случае недостаточным, необходим интервальный прогноз, т.е. отыскание такого диапазона 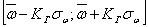 , в который с заданной вероятностью попадает значение значения качества управления w. Практически задача сводится к отысканию коэффициентов гарантии КГ из уравнения
, в который с заданной вероятностью попадает значение значения качества управления w. Практически задача сводится к отысканию коэффициентов гарантии КГ из уравнения
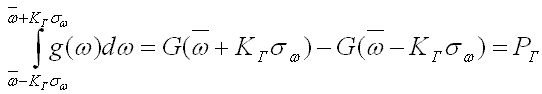 (44)
(44)
Для получения аналитического решения уравнения (44) необходимо аппроксимировать функцию g(w). Однако в связи с тем, что функция g(w) имеет разрыв в точке w = 1, аппроксимация ее известными непрерывными плотностями распределения не представляется возможной. Поэтому для отыскания решения уравнения (44) приходится использовать один из итерационных методов. Например, метод Ньютона. Зависимость коэффициента гарантии КГ и ширины полосы гарантированных значений качества управления от погрешности s прогноза параметра состояния при PГ = 0,95 представлены на рис. 33 и 34.
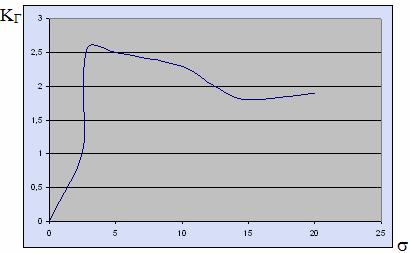
Рис.33 Зависимость коэффициента гарантии КГ от погрешности s параметра состояния
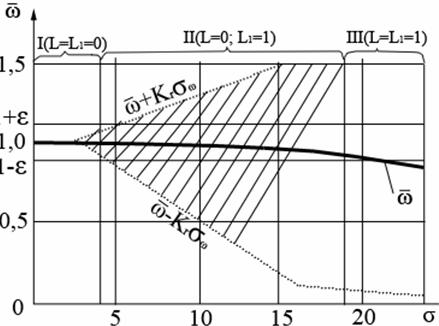
Рис.34. Зависимость ширины полосы гарантированных значений качества управления от погрешности s параметра состояния: I - зона нормы; II - зона опасности; III - зона тревоги
Как видно из рис.34, всю область изменения параметра s можно разбить на три зоны: 1 – зона нормы; II – зона опасности; III – зона тревоги.
В зоне I математическое ожидание качества управления со и полоса, в которую с гарантией 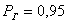 попадают все значения
попадают все значения 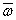 , целиком содержатся в требуемом интервале
, целиком содержатся в требуемом интервале 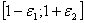 , поэтому ее называют зоной нормы.
, поэтому ее называют зоной нормы.
В зоне II значения 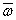 по-прежнему находятся в интервале
по-прежнему находятся в интервале 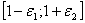 , но полоса
, но полоса 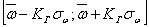 хотя бы одной из своих границ выходит за пределы, поэтому ее называют зоной опасности.
хотя бы одной из своих границ выходит за пределы, поэтому ее называют зоной опасности.
В зоне III значения 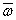 выходят за пределы вышеуказанного интервала и, как принято ранее, она считается зоной тревоги.
выходят за пределы вышеуказанного интервала и, как принято ранее, она считается зоной тревоги.
Таким образом, значение диалогового сигнала опасности 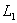 может быть определено следующим образом:
может быть определено следующим образом:
0, если 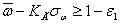 и
и 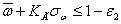
1, если 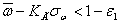 и
и 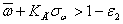
В реальных процессах необходимо учитывать возможность одновременного изменения обоих параметров 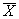 и σ, а также границ желаемого и допустимого диапазонов.
и σ, а также границ желаемого и допустимого диапазонов.
4.2. Модели формирования погрешностей технологических процессов
В реальных условиях любой технологический процесс совершается под воздействием многих случайных возмущений, зависящих от колебаний величины припуска на обработку, твердости материала заготовки, тепловых и силовых деформаций технологической системы и т.д.
В качестве критерия точности обработки деталей может быть принят показатель качества, учитывающий отклонения размеров в фиксированном сечении. При этом предполагается, что погрешностями формы детали в продольном и поперечном сечениях в задачах управления обработкой можно пренебречь, например, когда точность формы обеспечивается технологически. Примером такого процесса является обработка колец подшипников на токарных и шлифовальных автоматах.
Величину показателя качества, т.е. размера детали, обработанной в i-ом цикле (что эквивалентно отклонению размера детали от некоторого номинала) можно записать следующим образом:
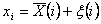
где X - уровень размерной настройки станка в i-ом цикле или математическое ожидание размера детали; 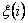 - случайное отклонение размера детали от уровня настройки.
- случайное отклонение размера детали от уровня настройки.
Известно, что основными причинами смещения уровня настройки являются тепловые деформации системы СПИД и размерный износ режущего инструмента. Тепловые деформации зависят от конструкции отдельных узлов станка, количества охлаждающей жидкости и степени ее загрязнения, протяженности температурных размерных цепей, характеристики и степени затупления режущего инструмента и режима правки, величины подач, скорости и глубины резания, материала и размера заготовок, температуры окружающей среды, сил трения, количества и качества смазки и т.д.
Силовые деформации технологической системы зависят от жесткости стыков, глубины резания, величины подачи, размера, твердости и качества заготовки, качества и размеров режущего инструмента, степени его затупления и характера правки, скорости резания, степени нагревания узлов станка, смазки и т.д.
Размерный износ режущего инструмента, например, при круглом шлифовании зависит не только от метода шлифования, но и от глубины резания, величины продольной подачи, окружной скорости детали, ее диаметра, твердости и качества материала заготовки, качества шлифовального круга его диаметра и степени затупления, метода и режима правки круга, геометрии правящего инструмента, скорости резания, вибрации и т.д.
В реальных технологических процессах смещение размерной настройки технологического оборудования вызывается совокупным действием многих факторов, однако, как правило, один из них имеет доминирующее значение. Поэтому можно ожидать, что указанные ниже модели окажутся подходящими для описания процесса настройки в широкой области технологических процессов. Кроме того, весьма типичной является ситуация, когда интенсивные тепловые деформации системы СПИД сопровождаются значительным износом инструмента, но рассеивание случайной величины износа в каждом цикле невелико и процесс износа можно считать неслучайным.
С учетом изложенных факторов процессы смещения настройки могут быть описаны тремя математическими моделями [6].
Модель 1 - стационарный случайный процесс, наложенный на неслучайную линейную функцию.
Примерный вид одной реализации процесса, характерного для этой модели, представлен на рис. 35. Основными характеристиками модели 1 являются: а - интенсивность неслучайного смещения настройки, приходящаяся на одну деталь (тренд); К(τ) - корреляционная функция случайной функциональной составляющей; 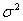 - дисперсия собственно случайной составляющей.
- дисперсия собственно случайной составляющей.

Рис.35. График погрешности обработки при модели 1
Математическое ожидание процесса X(i), описанного моделью 1 , есть неслучайная функция
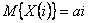
Дисперсия этого процесса
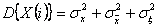
Модель 2 – нестационарный случайный процесс с независимыми приращениями. На рис.36 представлена реализация процесса, характерного для этой модели. Его основными характеристиками являются: 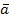 -математическое ожидание интенсивности смещения настройки, приходящееся на одну деталь;
-математическое ожидание интенсивности смещения настройки, приходящееся на одну деталь; 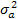 - дисперсия интенсивности смещения настройки по реализации;
- дисперсия интенсивности смещения настройки по реализации; 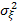 - дисперсия собственно-случайной составляющей.
- дисперсия собственно-случайной составляющей.
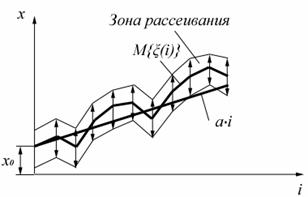
Рис.36. График погрешности обработки при модели 2
Дисперсия этого процесса - линейная функция времени
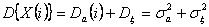
Математическое ожидание процесса есть неслучайная функция
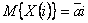
Модель 3 - стационарный случайный процесс, наложенный на случайную линейную функцию. Случайная величина а, определяющая интенсивность смещения настройки, приходящаяся на одну деталь (тренд), остается постоянной в пределах одной реализации случайного процесса, но меняется от реализации к реализации (a=const по реализации, a=var по ансамблю). Основными характеристиками модели (рис.37) являются: 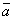 - математическое ожидание интенсивности смещения настройки, приходящееся на одну деталь;
- математическое ожидание интенсивности смещения настройки, приходящееся на одну деталь; 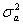 - дисперсия интенсивности смещения настройки по ансамблю; Кх(τ) - корреляционная функция случайной функциональной составляющей;
- дисперсия интенсивности смещения настройки по ансамблю; Кх(τ) - корреляционная функция случайной функциональной составляющей; 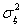 - дисперсия собственно-случайной составляющей.
- дисперсия собственно-случайной составляющей.
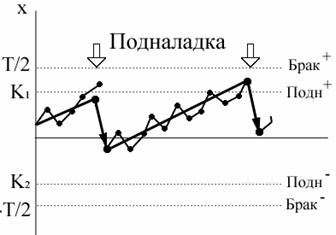
Рис.37 . График погрешности обработки при модели 3
Математическое ожидание процесса есть неслучайная линейная функция времени
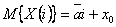
Дисперсия этого процесса представляет собой квадратичную функцию времени
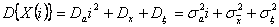
Выбор математической модели осуществляется обычно после предварительного исследования технологических процессов с целью установления степени его отлаженности, сбора статических данных в условиях действующего производства и их обработки.
4.3. Точность подналадочных систем
Подналадка представляет собой одну из форм осуществления размерных обратных связей при обработке на металлорежущих станках. К подналадкам относятся измерительные приборы, которые через цепь обратной связи вызывают изменение настройки металлорежущего станка или измерительного устройства, управляющего работой станка, когда значение контролируемого параметра выходит за допустимые границы или отклоняется от заданного значения. Подналадочные системы применяются в основном при обработке методом "на проход", в частности, при сквозном бесцен троном шлифовании. Однако в сочетании с жесткими упорами или средствами контроля в процессе обработки (например, с чувствительными упорами) подналадчики могут применяться и при врезных процессах.
Подналадка может осуществляться по результатам контроля группы деталей (частный случай - подналадка по одной детали), по положению центра группирования случайных погрешностей, при этом наиболее часто применяются методы подналадки по среднему арифметическому значению или по медиане выборки деталей.
Подналадочный импульс А формируется в зависимости от принятого для данного технологического процесса алгоритма подналадки.
4.3.1. Подналадка по N - деталям подряд
Подналадочный импульс подается тогда, когда N деталей подряд оказались за пределами сигнальной границы. Наиболее распространен данный алгоритм подналадки для N=1. В этом случае
 (45)
(45)
где А - амплитуда подналадочного импульса; К1 , К2 - положения нижней и верхней сигнальной границ относительного номинального значения размера изделия, принятого за нуль.
Если расстояние между сигнальными границами свести к нулю и совместить их с серединой поля допуска Т, то получим метод пульсирующей подналадки. В этом случае Подналадочный импульс подается на каждом такте технологического процесса. График изменения размеров деталей при подналадке по одной детали представлен на рис. 38.
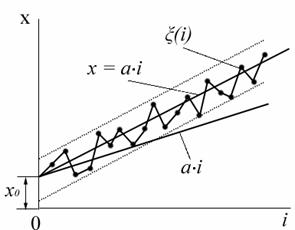
Рис.38. Схема подналадки по одной детали
Для формирования подналадочного импульса по N -деталям подряд введем вспомогательную функцию
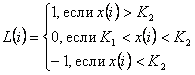 (46)
(46)
Функция L(i) эквивалентна функции тревоги, рассмотренной ранее. С учетом (45) и (46) алгоритм подналадки по N - деталям подряд можно представить в виде
A(i) = AL(i). (47)
График изменения размеров деталей при N=4 показан на рис.39.
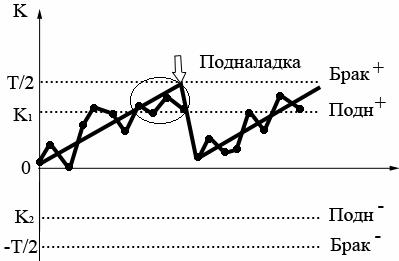
Рис.39. Схема подналадки по четырем деталям подряд
На стадии проектирования подналадочной системы необходимо исследование исходного технологического процесса, по результатам которого производится прогнозная оценка точности разрабатываемого устройства. Структура предельной погрешности при подналадке по одной детали представлена на рис. 40. Прогнозное значение предельной погрешности подналадки может быть представлено в виде
δ= А+2В + 6σ+Е, (48)
где А - величина подналадочного импульса;
В - зона формирования подналадочного импульса (зона опасности);
σ - величина собственно случайных погрешностей обработки. Диапазоны, ограниченные интервалами Зσ, представляют собой зоны тревоги, т.е. зоны, в которых вероятность подналадки равна 1;
Е - паспортная величина погрешности измерительного преобразователя измерительной позиции поднададчика.
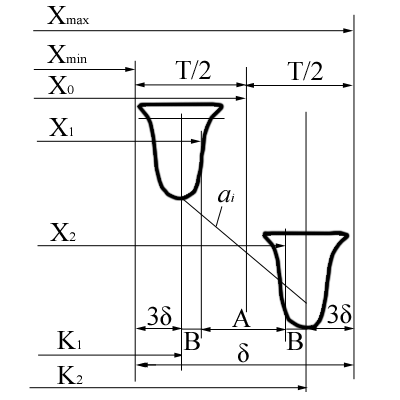
Рис.40. Структура предельной погрешности при подналадке по одной детали
Интервалы зон тревоги и опасности определяются параметрами исходного технологического процесса. При нормальном законе распределения случайных погрешностей обработки и измерения величина σ определяется по известной формуле
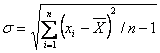 ,
,
где n - число обработанньгх деталей за период наблюдения.
Интервал зоны формирования подналадочного импульса В может быть найден из выражения
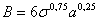
где a - величина функциональной погрешности обработки, приходящаяся на одну деталь.
Датчик предельных размеров измерительной позиции полналадчика настроен на нижнюю ki и верхнюю К2 сигнальные границы и фиксирует выход размера детали только за эти границы. При выходе размера детали за сигнальные границы УКВ управляет исполнительными механизмами станка (или несколько станков), которые осуществляют подналадочные перемещения.
Под влиянием неконтролируемых возмущений сигнальные границы К1 и К2 могут смещаться, занимая некоторые текущие положения Х1 и Х2. Информация о влиянии функциональных воздействий на технологический процесс вводится в вычислительное устройство [28] дискретно через временной коммутатор. Временной коммутатор подключает датчики одного или нескольких станков через заданные промежутки времени. Этот временной интервал может изменяться в зависимости от интенсивности изменения поля рассеивания δ и a.
Подналадочная система считается работающей удовлетворительно, если обеспечивается условие δ < Т.
Блок-схема алгоритма управления точностью обработки с помощью подналадочной системы показана на рис.41. Выполнение программы начинается с ввода исходных данных, представляющихсобой константы, вспомогательные параметры не изменяющиеся во времени, например, номинальный размер, Т/2 и другая информация (оператор 1). Исходная информация дополняется текущей информацией от датчиков, регистрирующих состояние технологической среды в тот или иной момент времени (оператор 2). На основании поступившей информации вычисляются среднеквадратическое отклонение σ, величина функциональной погрешности, приходящаяся на одну деталь, интервал формирования подналадочного импульса В, наибольший Хmаx и наименьший Xmin предельные размеры детали, положение нижней К1 и верхней К2 сигнальных границ (оператор 3). Далее определяются текущие нижняя Х1i и верхняя X2i сигнальные границы, в которых допускается смещение уровня настройки (оператор 4) и фактическое значение контролируемого параметра Xi (оператор 5). В связи с сужением возможного диапазона смещения настройки под влиянием случайных факторов, из-за увеличения составляющих предельной погрешности от быстропротекающих процессов и погрешности формы, может наступить момент, когда проведение подналадок станет невозможным. Это соответствует состоянию системы, когда достигается положение К1=К2, т.е. сигнальные границы стягиваются в точку. Поэтому программой предусмотрена проверка возможности проведения подналадки (операторы 6 и 7).
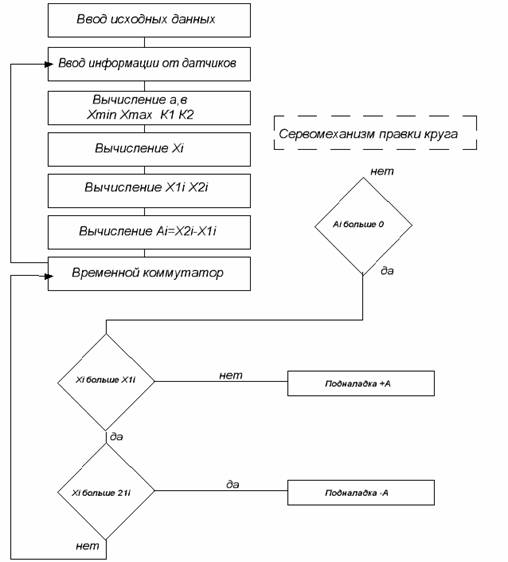
Рис.41. Блок-схема алгоритма управления точностью обработки
Если возможность имеется, то определяется направление подналадочного импульса А, и выдается команда на исполнение подналадки (операторы 8-11).
4.3.2. Подналадка по среднему арифметическому
Подналадочные системы не могут компенсировать влияние собственно случайных погрешностей обработки. В условиях данного технологического процесса при различных методах подналадки могут изменяться любые составляющие предельной погрешности (например А, В, Е), за исключением 6σ. Постоянство составляющей 6σ и является выражением того, что подналадочные системы не в состоянии компенсировать собственно случайные погрешности обработки. Однако при соответствующем выполнении подналадочной системы можно в значительной степени избежать влияние грубых погрешностей обработки, устранить возможность возникновения повторных импульсов и существенно уменьшить величину параметра В (последние два фактора зависят от собственно случайных погрешностей, к которым относятся и грубые погрешности).
При подналадке по среднему арифметическому при каждом такте технологического процесса анализируется выборка деталей объемом N. Подналадочный импульс подается, когда среднее арифметическое выборки деталей X выходит за установленные сигнальные границы, т.е.
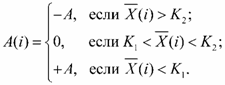 (50)
(50)
График изменения размеров деталей при подналадке по среднему арифметическому представлен на рис.42.
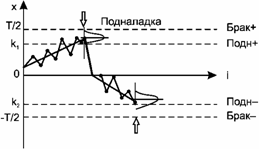
Рис. 42. График изменения размеров деталей при подналадке по среднему арифметическому
Структура предельной погрешности подналадки по среднему арифметическому выборки деталей такая же, как и при подналадке по одной детали, но некоторые составляющие изменяют свое значение. Предельная погрешность подналадки по среднему арифметическому размеру деталей выборки может быть выражена следующим образом
δc = A + 6σ + 2Bc + Ec ; (51)
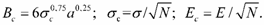
Таким образом, выражение (51) в окончательном виде может быть представлено так
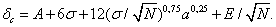 (52)
(52)
4.3.3. Подналадка по медиане
При подналадке по медиане на каждом такте технологического процесса анализируется выборка деталей объемом N и осуществляется вычисление медианы ХM эмпирической кривой распределения размеров. Подналадочный импульс подается, если размеры более чем N/2 деталей в выборке перешли за установленные сигнальные границы, т.е.
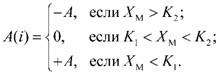 (53)
(53)
Основное преимущество подналадки по медиане по сравнению с подналадкой по среднему арифметическому заключается в том, что на ее точность влияние грубых погрешностей размеров практически не сказывается.
Суммарная погрешность при подналадке по медиане имеет такую же структуру, как и при подналадке по одной детали и среднему арифметическому. Разница заключается только в величинах третьего и четвертого слагаемых, которые уменьшаются при усредненных подналадках. Поскольку удельный вес четвертого слагаемого весьма невелик, то погрешности при различных методах подналадки различаются в основном значением параметра В.
Предельная погрешность подналадки по медиане выборки деталей определяется из выражения:
δм = A + 6σ + 2Bм + Eм ; (54)
где 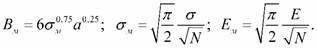
Окончательно выражение (54) преобразуется к виду
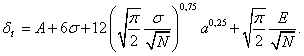 (55)
(55)
График изменения размеров деталей при подналадке по медиане выборки деталей представлен на рис. 43.
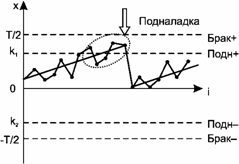
Рис. 43. График изменения размеров деталей при подналадке по медиане
4.3.4. Ограничения па величину подналадочного импульса
Анализ зависимости (48), (52) и (55) показывает, что для уменьшения величины предельной погрешности подналадки необходимо уменьшение величины подналадочного импульса. Возможность уменьшения параметра А ограничивается несколькими факторами, главным из которых является порог чувствительности исполнительных органов станка. Дело в том, что при малых скоростях перемещения исполнительных органов наблюдается [21] резко выраженная неравномерность движения, которое происходит прерывисто, с периодически чередующимися срывами и остановками. Такого рода скачкообразное движение весьма характерно дня технологических систем, когда необходимо обеспечить перемещения со скоростями порядка нескольких миллиметров в минуту и ниже. Подобные перемещения имеют место при подналадке.
Рассмотрим модель исполнительного органа станка, представляющую собой упругую систему (рис.44). Эта система состоит из задающего устройства, имеющего постоянную скорость движения V, и твердого тела (платформы, шлифовальной или ведущей бабки, каретки и т.д.) массой m. При сообщении подналадочного импульса задающее устройство перемещает платформу посредством привода с приведенной жесткостью С.
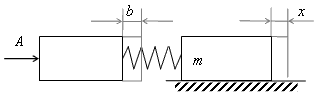
Рис. 44. Модель привода исполнительного органа станка
Величина перемещения задающего устройства b является реакцией - этого устройства на входное воздействие в виде подналадочного импульса А. Очевидно, что пока не будет преодолена сила статического трения F0 движение передвигаемого узла начаться не может и x=0. Иначе, движение произойдет, если b<F0/C . В идеальном случае, т.е. при отсутствии сил статического и кинетического трения b=x. В реальных условиях возникает погрешность перестановки ∆, которая определяется величиной рассогласования (величиной порога чувствительности рабочего органа)
∆=b-x (56)
где ∆ - перемещение рабочего органа станка, например, шлифовальной бабки.
Подналадка произойдет, если величина подналадочного импульса А будет больше порога чувствительности передвигаемого узла
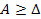 (57)
(57)
Величина перемещения b задающего устройства может быть определена [21] из выражения
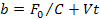 (58)
(58)
где V - скорость перемещения задающего устройства.
Величина перемещения х рабочего органа определится уравнением свободного движения тела
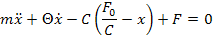
где F - сила кинетического трения; 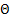 - коэффициент затухания.
- коэффициент затухания.
Решение этого уравнения при малом затухании может быть принято как
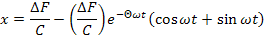
что к моменту остановки (после прекращения подналадочного воздействия) при 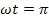
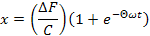
В этом выражении 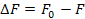 представляет собой разность сил статического и кинетического трения.
представляет собой разность сил статического и кинетического трения.
В предельном случае при 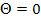 величина перемещения равна
величина перемещения равна
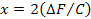
Таким образом, во всех случаях величина перемещения х равна
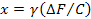 (59)
(59)
где 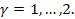 При
При 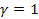 принимает наименьшее значение, а при
принимает наименьшее значение, а при 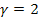 - наибольшее.
- наибольшее.
Наибольшее возможное рассогласование в положениях задающего устройства b и передвигаемого узла x определяется из условия, что величина перемещения задающего устройства, которая характеризуется выражением (58), при t = 0 принимает максимальное значение, т.е.
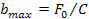 (60)
(60)
а величина перестановки х из выражения (59) при 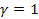 - минимальное, т.е.
- минимальное, т.е.
xmin = ΔF0 / C, (61)
Следовательно, условие (56) с учетом (60) и (61) можно представить в виде
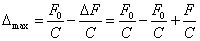
или
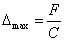
Величина F представляет собой
F = (μП – μД)N,
где N – нормальное усилие на направляющих передвигаемого узла.
В окончательном виде выражение (56) может быть представлено как
Δ = (μП – μД)N/C, (62)
где μП и μД – коэффициенты трения покоя и движения соответственно.
В случае, если нормальная сила определяется только собственным весом узла, передвигаемого по горизонтальным направляющим, порог чувствительности
Δ = (μП – μД)mg/C,
Соответственно условие подналадки (57) можно переписать в виде
А³ (μП – μД)mg/C. (63)
Величина жесткости привода С определяется из выражения
С = ES/l, (64)
Е – модуль упругости первого рода; S – площадь поперечного сечения элемента привода (винта, штока, поршня и т.д.); l – длина неразрезанной части винта или рабочая длина штока поршня.
Значения коэффициентов трения покоя и движения в зависимости от материалов трущихся пар представлены в табл. 2.
Условие (63) справедливо в случае перемещения исполнительных органов станка с докритическими скоростями. В случае перемещения узла со скоростью больше критического значения характер его движения становится плавным и равномерным. На рис.45 верхняя штриховая линия соответствует равномерному перемещению заданного устройства при критических скоростях, а сплошная - прерывистому перемещению узла с докритическими скоростями при чередовании скачков и остановок.
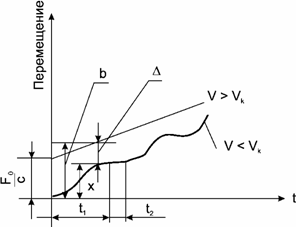
Рис. 45. Характер перемещения исполнительного органа станка при малых скоростях
Таблица 2
Значения коэффициентов трения покоя и движения
|
Материал трущейся пары |
Коэффициент трения покоя μП |
Коэффициент трения движения μД |
|
Чугун – чугун |
0,25–0,27 |
0,15–0,17 |
|
Сталь – чугун |
0,20–0,25 |
0,05–0,15 |
|
Сталь – сталь |
0,13–0,16 |
0,05–0,10 |
|
Сталь – бронза |
0,15–0,20 |
0,10–0,15 |
|
Чугун – бронза |
0,20–0,25 |
0,15–0,17 |
|
Чугун – текстолит |
0,25–0,30 |
0,17–0,20 |
|
Чугун - фторопласт |
0,05–0,07 |
0,02–0,03 |
Заданные свойства системы (жесткость, масса, коэффициент относительного рассеяния энергии колебаний) и известные характеристики силы трения определяют значение критической скорости движения. Для практических расчетов рекомендуется формула для определения критической скорости [21].
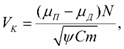 (65)
(65)
где y – относительное рассеяние энергии при колебаниях.
Значения относительного рассеяния энергии при колебаниях в отдельных элементах привода представлены в табл. 3.
Критические скорости исполнительных органов станка шлифовальной группы в зависимости от их параметров колеблются в пределах от 20 до 60 мм/мин, а скорости рабочих подач – от 0,8 мм/мин (при черновом шлифовании) до 0,1 мм/мин (при чистовом шлифовании). Потому при шлифовании следует учитывать наличие порога чувствительности и ожидать скачкообразного перемещения исполнительного органа. Практическую величину скачка можно определить как
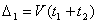 (66)
(66)
где V - действительная скорость перемещения шлифовальной бабки; t1 - продолжительность скачка; t2 - продолжительность остановки.
Таблица 3
Значения коэффициентов относительного рассеяния энергии при колебаниях
Продолжительность скачка можно определить по формуле
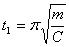
а продолжительность остановки
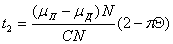
где 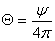 .
.
4.3.5. Оценка точности подналадки методом имитационного моделирования
На стадии проектирования системы управляющего контроля выбор ее структуры, метода и параметров подналадки основан на минимизации погрешности обработки управляемого технологического процесса. Натурные испытания с реальными технологическими процессами требуют аппаратурной реализации (макетирования) системы управляющего контроля, больших финансовых затрат, вызывают проблемы с контролем деталей и статистической обработкой результатов. В этих условиях целесообразно проводить имитационное моделирование на ЭВМ хода технологического процесса с системой управляющего контроля. Имитация на ЭВМ представляет собой численный метод проведения экспериментов с математическими моделями, описывающими поведение реального технологического процесса и взаимодействующей с ним системы управляющего контроля. В результате экспериментов с имитационными моделями можно оценивать статистические параметры погрешности технологического процесса при его управлении по различным алгоритмам и при различных управляющих воздействиях, что позволяет выбрать оптимальную по точности структуру системы управляющего контроля, метод управления (в частности, метод и параметры подналадки).
Рассмотрим реализацию этой идеи на примере программы SHLIF, алгоритм которой приведен на рис.46.
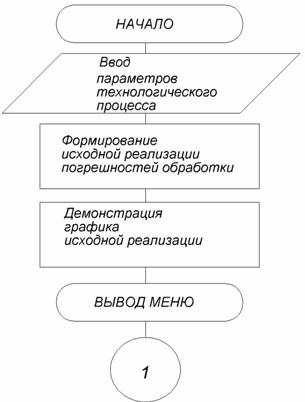
Рис.46. Алгоритм расчета точности подналадки методом имитационного моделирования (начало)
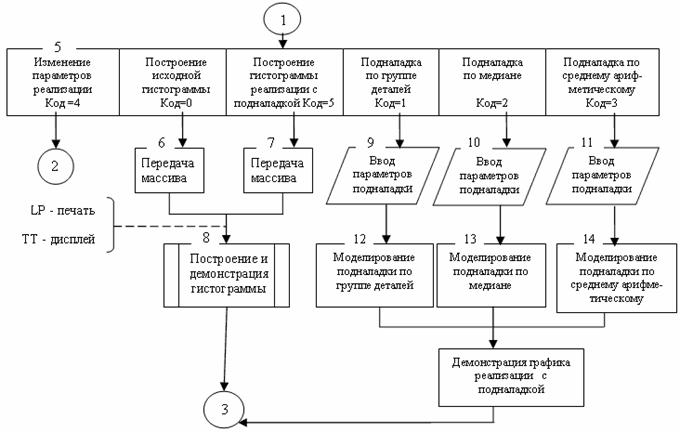
Рис.46. Алгоритм расчёта точности подналадки методом имитационного моделирования (окончание)
В блоке 1 программа для моделирования реализации погрешности обработки технологического процесса без управления запрашивает его статистические параметры: число обрабатываемых деталей N (длину реализации), начальный уровень настройки М, среднеквадратическое отклонение собственно случайных погрешностей обработки S, функциональную составляющую погрешности обработки, приходящуюся на одну деталь a. Для моделирования подналадки запрашивается верхняя сигнальная граница настройки К1 и нижняя сигнальная граница настройки К2. Пример ввода исходной информации приведен на рис.47.

Рис.47. Пример ввода исходной информации при имитационном моделировании подналадки и распечатка меню программы
Блок 2 формирует реализацию погрешности обработки технологического процесса без управления (исходную), представляя ее "МОДЕЛЬЮ 1".
Блок 3 демонстрирует на дисплее график исходной реализации, его пример приведен на рис.48.
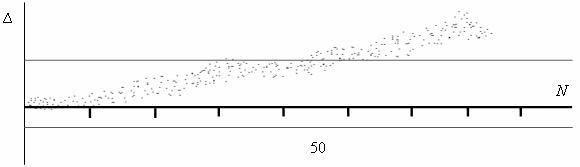
Рис.48. График смоделированной программы SHLIF исходной реализации погрешности обработки анализируемого технологического процесса
Далее выводится па дисплее меню (блок 5, пример на рис.47) и запрашивается код перехода. Имеются следующие возможности дальнейшей работы:
- изменение параметров подналадки, при этом осуществляется возврат к блоку;
- построение гистограммы и демонстрация статистических показателей точности технологического процесса (блок 8, примеры распечатки приведены на рис. 49, 50);

Рис. 49. Точностные характеристики анализируемого технологического процесса без подналадки, смоделированного программой SHLIF
- моделирование подналадки по группе деталей, по медиане или по среднему арифметическому, при этом из исходной реализации в соответствии с алгоритмами, описанными в разд. 4.3.1, 4.3.2., 4.3.3, формируется реализация погрешности обработки технологического процесса с подналадкой.
Блок 15 приводит демонстрацию графиков этих реализаций. Их примеры приведены на рис. 51, 52, 53, черточками на графиках показаны моменты подналадки.
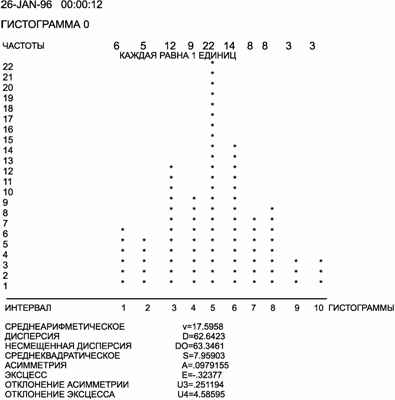
Рис. 50. Точностные характеристики технологического процесса с подналадкой по группе деталей
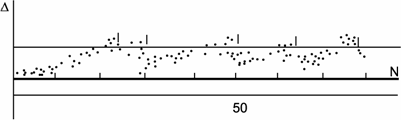
Рис. 51. График реализации погрешности обработки технологического процесса с подналадкой по 4-м деталям подряд
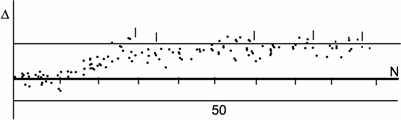
Рис. 52. График реализации погрешности обработки технологического процесса с подналадкой по медиане с объемом выборки N=4
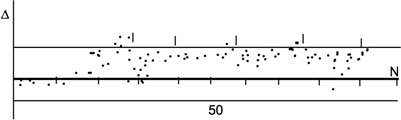
Рис. 53. График реализации погрешности обработки технологического процесса с подналадкой по среднему арифметическому с объемом выборки N=4
Затем происходит возврат на меню программы (блок 4), здесь возможно по коду 5 перейти к построению гистограммы реализации погрешности обработки и выводу статистических параметров оценок точности, пример которых приведен на рис. 50. По запросу программы, вводя параметры Р или ТТ, вывод гистограммы и статистической таблицы осуществляется на печать или дисплей соответственно.
Экспериментируя с имитационной моделью на ЭВМ, можно оценить статистические параметры точности технологического процесса с подналадкой, выбрать метод подналадки и ее параметры (объем выборки и величину импульса подналадки) из условия минимизации погрешности обработки.

