3. ДИНАМИЧЕСКИЙ АНАЛИЗ СИСТЕМ АКТИВНОГО КОНТРОЛЯ
3.1. Станок как динамический объект управления
3.2. Динамические погрешности приборов активного контроля
3.3. Динамическая погрешность суммирования сигналов
3.1. Станок как динамический объект управления
Точность систем активного контроля существенно связана с динамикой объекта управления. Динамические свойства объекта управления необходимо учитывать при установлении параметров цикла обработки детали.
Ниже рассмотрена динамика объекта управления (активного контроля размеров детали) на станках, производящих шлифование деталей методом врезания. К объекту управления относят процесс шлифования и механическую часть станка, связанную с подачей шлифовального круга и креплением обрабатываемой детали, а также саму деталь [10].
Реальный станок представляет собой сложную динамическую систему со значительным числом степеней свободы. Полное рассмотрение реальной системы затруднительно, а результаты такого анализа будут сложны для практического применения. Чтобы выявить основные причины, влияющие на изменение размера детали, рассмотрим упрощенную динамическую модель объекта с одной степенью свободы, изображена рис.21. Ограничить число степеней свободы станка в динамической модели можно на том основании, что деталь и инструмент в сечении, перпендикулярном оси вращения, имеют форму окружности, вследствие чего можно считать, что изменение размера происходит только под действием нормальной составляющей движения. Влиянием тангенциальной составляющей можно пренебречь, как величиной второго порядка малости.
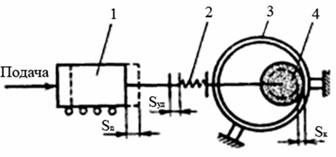
Рис. 21. Динамическая модель объекта управления: 1- шлифовальная бабка: 2 - упругая связь; 3 – обрабатываемая деталь: 4 - шлифовальный круг
Анализ динамической модели объекта активного контроля проводим в предположении, что станок представляет собой линейную упругую систему с сопротивлением, пропорциональным первой степени скорости; усилие резания пропорционально фактической толщине снимаемого слоя металла.
Объект управления при обработке неупругой детали, например, при шлифовании желоба наружного кольца подшипника (см. рис. 21) в соответствии с динамической моделью представляем как замкнутую систему, состоящую из пяти звеньев.
Первое звено - подача шлифовального круга. Входным сигналом звена является перемещение шлифовальной бабки SП, выходным сигналом - нормальная сила f, с которой шлифовальный круг воздействует на обрабатываемую деталь. Уравнение звена
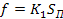
где К1 - жесткость системы, Н/м.
Второе звено - скорость износа шлифовального круга. Входным сигналом звена является нормальная сила , а выходным скорость износа шлифовального круга 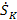 . Уравнение звена . Уравнение звена
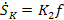
где К2 - степень износа шлифовального круга, М/(Н*с).
Третье звено - износ шлифовального круга. Входным сигналом звена является скорость износа шлифовального круга 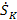 , а выходным - величина износа круга SК , т.е. это звено является интегрирующим, и операцию, которую оно производит, можно представить в виде , а выходным - величина износа круга SК , т.е. это звено является интегрирующим, и операцию, которую оно производит, можно представить в виде
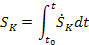
Четвертое звено – скорость съема припуска детали. Выходным сигналом звена является сила f, а выходным скорость съема припуска, т.е. скорость изменения размера детали 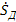 .Уравнение звена .Уравнение звена
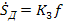
где К3 - удельный съем припуска, М/(Н*с).
Пятое звено - съем припуска детали. Входной сигнал - скорость съема припуска, выходной - величина снятого припуска Sд; за время шлифования. Уравнение звена
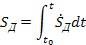
На основании полученных уравнений звеньев можно составить структурную схему объекта управления. Но поскольку структурная схема является графическим представлением зависимостей, имеющих место между изображениями по Лапласу для внешних возмущений и для переменных параметров этого объекта, то предварительно определим передаточные функции звеньев, которые представляют собой отношения упомянутых изображений.
Передаточная функция для:
- первого звена 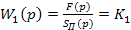
- второго звена 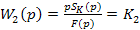
- третьего звена 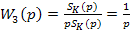
- четвертого звена 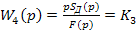
- пятого звена 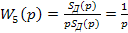
В соответствии с общим уравнением процесса шлифования
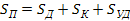
Где Sуд - величина упругих деформаций системы, и используя по данные передаточные функции, составляем структурную схему объекта управления (рис.22).
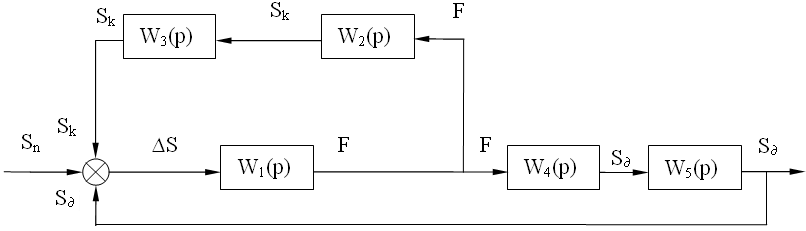
Рис. 22.Структурная схема объекта управления
На основе методов теории автоматического управления находим передаточную функцию разомкнутой системы, которая соответствует структурной схеме, где выходная величина – съем припуска SД:
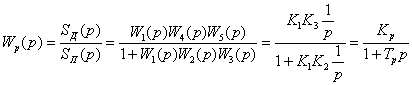 , ,
где Кр =К3 /К2 – коэффициент передачи разомкнутой системы объекта; Тр = 1/К1К2 – постоянная времени разомкнутой системы объекта.
Передаточная функция замкнутой системы объекта управления
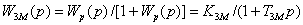 , ,
где К3М =Кр /(1 + Кр) = 1/[К1(К2 +К3)] – коэффициент передачи замкнутой системы объекта;
Т3M = Тр /(1 + Кр) = 1/[К1(К2 +К3)]- постоянная времени замкнутой системы объекта.
Таким образом, передаточная функция объекта управления при шлифовании неупругой детали соответствует апериодическому звену с постоянной времени Т3М и коэффициентом передачи К3М.
3.2. Динамические погрешности приборов активного контроля
Вибрация измерительных наконечников. Механическая измерительная система контактных приборов активного контроля в процессе шлифования находится в динамическом режиме вследствие изменения размера детали и действия вибраций. Частота и амплитуда вибраций измерительных наконечников приборов зависят от множества факторов: режимов обработки, характеристик режущего инструмента, погрешностей геометрической формы детали и т. д.
При внутреннем шлифовании колец подшипников на жестких опорах погрешность геометрической формы детали оказывает на динамику измерения более существенное влияние, чем при шлифовании в патроне. Экспериментальные работы показали, что при бесцентровом шлифовании на жестких опорах посадочных отверстий колец подшипников копируются геометрические отклонения формы базовой поверхности. Очевидно, такое же влияние существует и при шлифовании дорожек качения наружных колец, когда щлифуемая дорожка копирует погрешности геометрической формы наружной цилиндрической поверхности.
На рис.23 приведена схема бесцентрового шлифования на жестких опорах. Базовая поверхность шлифуемого кольца имеет контакт с жесткими опорами в точках А и В. Шлифуемая поверхность контактирует с абразивным кругом в точке Е и с измерительными наконечниками в точках С и О. Все отмеченные точки как обрабатываемой поверхности так и базовой поверхности кольца находятся в одной плоскости. Взаимное расположение точек. А, В, С, D определяется углами 2φ, φ, 0 и 0+180°.
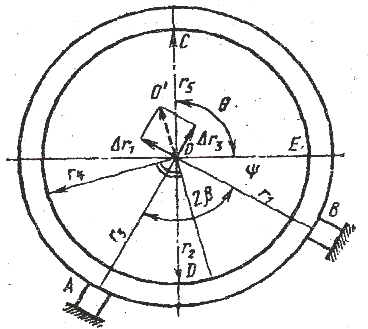
Рис.23.Схема бесцентрового внутреннего шлифования
Погрешности формы базовой поверхности вызывают изменение положения геометрического центра вращения кольца О. Перемещение центра вращения можно рассматривать как функцию мгновенных значений радиусов r1 и r3.
Перемещение центра и, следовательно, кольца имеет горизонтальную и вертикальную составляющие. Горизонтальная составляющая совпадает с направлением касательной в точке контакта изделия с измерительными наконечниками и оказывает на их колебание пренебрежимо малое влияние. Основное же влияние оказывает вертикальная составляющая. Суммируя вертикальную составляющую перемещения центра с величиной изменения мгновенных значений радиусов r2 и r4 , найдём общую величину перемещения измерительных наконечников, вызванную погрешностью форы кольца.
Вибрация наконечников, вызываемая погрешностью формы детали, зависит от значения углов 2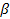 , , 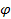 , 0. Доля влияния каждой гармоники на вибрацию наконечника характеризуется своим коэффициентом передачи , 0. Доля влияния каждой гармоники на вибрацию наконечника характеризуется своим коэффициентом передачи
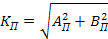
В рассматриваемом случае
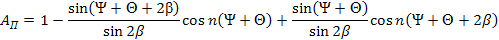
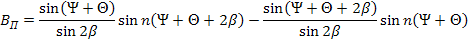
где n- номер гармоники.
По данной формуле были вычислены значения КП для распространенных углов наладки жестких опор при расположении измерительных наконечников в точках C и D.
Значения параметров вибрации измерительных наконечников процессе шлифования можно определить только экспериментально. Вызывают ли такие значения вибрации отрыв измерительного наконечника от детали, можно выяснить, воспользовавшись выражением критической частоты:
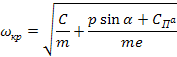
которое на основании равенства Р = mg можно записать как
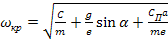 (10) (10)
где СП - приведенная жесткость пружин датчика; m - масса подвижной системы; g - ускорение силы тяжести; e - амплитуда вибраций; 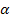 - угол наклона измерительного стержня к горизонтальной оси; - угол наклона измерительного стержня к горизонтальной оси; 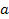 - предварительное растяжение пружины; Р - сила тяжести подвижной системы. - предварительное растяжение пружины; Р - сила тяжести подвижной системы.
Из формулы (10) следует, что увеличивать измерительное усилие 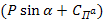 целесообразно только за сёт упругих связей. Увеличение силы тяжести подвижной системы измерительной головки (при положительном значении sinα ) лишь уменьшает значение критической частоты. целесообразно только за сёт упругих связей. Увеличение силы тяжести подвижной системы измерительной головки (при положительном значении sinα ) лишь уменьшает значение критической частоты.
Минимально возможное значение критической частоты получим из формулы (10) при отсутствии упругих связей или при неограниченном увеличении массы подвижной системы, т.е.
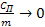 и и 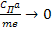
тогда
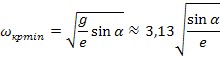
(амплитуда вибраций выражается в микрометрах).
Минимальное критическое ускорение для рассматриваемого случая
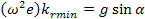
откуда следует, что при верхнем вертикальном расположении измерительного стержня минимальное критическое ускорение равно ускорению силы тяжести.
Динамический анализ двухконтактной измерительной головки. В промышленности широко используют двухконтактные приборы активного действия. Динамический анализ даухконтактных измерительных головок с независимым подвесом измерительных стержней сводится к анализу одноконтактных. Ниже приводится анализ двухконтактных измерительных головок с зависимым I подвесом измерительных стержней, т.е. упругой связью между ними. Анализ распространяется и на приборы с так называемыми плавающими корпусами.
Расчетная схема нагружения двухконтактной измерительной головки с зависимым подвесом измерительных стержней приведена на рис. 24. Измерительные стержни 2 (верхний) и 7 (нижний) контактируют с обрабатываемой поверхностью детали 1 в точках А и В, которые соответственно и выбирают за начало координат. Стержень 7 подвешен на двух плоских пружинах 5 к корпусу прибора. Стержень 2 подвешен на двух плоских пружинах 4 к стержню 7. Измерительное усилие обеспечивается с помощью пружин 3 и 6.
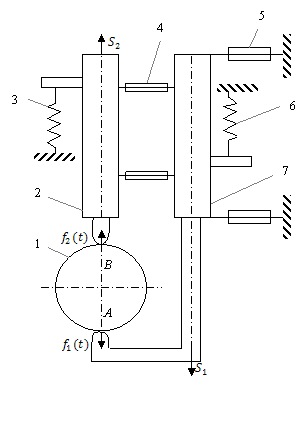
Рис. 24. Расчетная схема нагружения измерительной головки
Характер вибраций датчиков различен в зависимости от конкретных условий работы. Для удобства исследования динамических характеристик закон движения точки соприкосновения измерительного стержня с измеряемой поверхностью запишем в виде гармонических колебаний:
для нижнего измерительного стержня 7
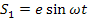 (11) (11)
для верхнего измерительного/ стержня 2
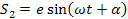 (12) (12)
Динамический анализ проводим для каждого стержня в отдельности при условии, что другой стержень движется без отрыва от детали. Внутренним трением упругих элементов пренебрегаем.
Динамический анализ нижнего измерительного стержня.
Механическая схема датчика представляет собой систему с упругими связями и может быть описана уравнением Лагранжа II рода:
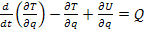 (13) (13)
где Т - кинетическая энергия системы; U - потенциальная энергия системы; q - обобщенная координата системы; 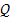 - обобщенная сила системы. - обобщенная сила системы.
Для нижнего стержня кинетическая и потенциальная энергии могут быть найдены из выражений
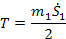
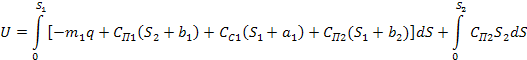
где 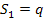 - перемещение стержня; m1 - масса измерительного стержня; - перемещение стержня; m1 - масса измерительного стержня; 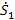 - скорость перемещения стержня; - скорость перемещения стержня; 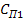 - жесткость плотских пружин 5; - жесткость плотских пружин 5; 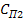 - жесткость плоских пружин 4; - жесткость плоских пружин 4; 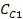 - жесткость спиральной пружины 6; a1 - предварительное растяжение спиральной пружины 6; b1 - предварительный изгиб плоских пружин 5; b2 -предварительный изгиб плоских пружин 4; q - ускорение силы тяжести. - жесткость спиральной пружины 6; a1 - предварительное растяжение спиральной пружины 6; b1 - предварительный изгиб плоских пружин 5; b2 -предварительный изгиб плоских пружин 4; q - ускорение силы тяжести.
Подставляя эти выражения в уравнение (13) и принимая, что 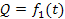 - внешняя сила, действующая на стержень (реакция детали), получим - внешняя сила, действующая на стержень (реакция детали), получим
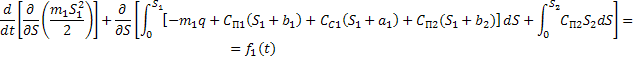 (14) (14)
После преобразования будем иметь
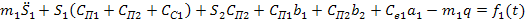 (15) (15)
Обозначим: 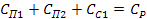 - приведенная жесткость; - приведенная жесткость; 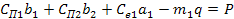 - приведенная статическая сила. Тогда окончательно получим - приведенная статическая сила. Тогда окончательно получим
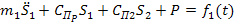 (16) (16)
Полученное равенство является дифференциальным уравнением движения измерительного стержня 7 без учета сил трения и влияния вибраций станка на корпус измерительной головки.
Критическая частота вибраций. Под критической частотой понимают частоту, при которой начинается разрыв кинематической пары измерительной цепи при определенной амплитуде. В данном случае разрыв возможен только в месте соприкосновения стержня 7 с измеряемой поверхностью (точка А на рис. 24).
Отрыв стержня 7 от измеряемой поверхности становится возможным при исчезновении реакции детали на измерительный наконечник, т.е. при f1(t) = 0 . Тогда из уравнения (16) получим критическую величину ускорения
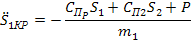 (17) (17)
Используя законы движения (11) и (12), перепишем равенство (17)
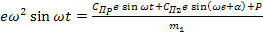 (18) (18)
Наибольшее ускорение подвижная система получит при 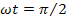 . .
Тогда
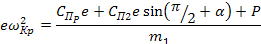
Отсюда
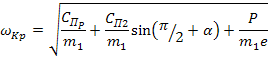 (19) (19)
Рассмотрим предельно возможные значения второго слагаемого подкоренного выражения в зависимости от значений угла α:
1) α =0 в случае овальности или другой четной гармоники погрешности формы детали:
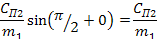
2) 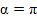 в случае перемещения детали, вызванного вибрацией, а также при смещении детали из-за погрешностей формы базовой поверхности при шлифовании на жестких опорах: в случае перемещения детали, вызванного вибрацией, а также при смещении детали из-за погрешностей формы базовой поверхности при шлифовании на жестких опорах:
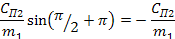
Следовательно, минимальное значение критической частоты, на которое следует ориентироваться при анализе соответствующих измерительных головок, имеет вид
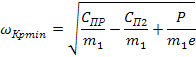
Так как 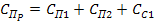 , то можно записать , то можно записать
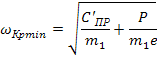 , ,
где
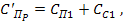
Таким образом, при определении критической частоты нижнего стержня упругая связь с верхним стержнем не учитывается.
Динамический анализ верхнего измерительного стержня.
Аналогично предыдущему составим дифференциальное уравнение, движения для верхнего стержня 2:
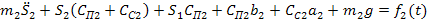 (20) (20)
Обозначим 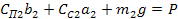 - приведенная статическая сила. - приведенная статическая сила.
Тогда уравнение (20) примет вид
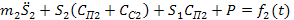 . .
При условии отрыва 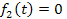 определяем критическое ускорение, из которого получаем выражение критической частоты определяем критическое ускорение, из которого получаем выражение критической частоты
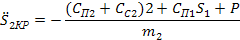 (21) (21)
Для упрощения дальнейших выкладок изменим начало отсчета так, чтобы
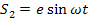 (22) (22)
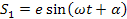 (23) (23)
Подставляем формулы (22) и (23) в уравнение (21) при 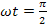
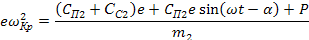
Отсюда
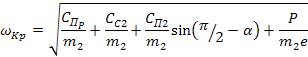
Минимальное значение критической частоты будет при 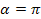 , когда , когда 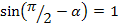 : :
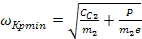 (24) (24)
В этом случае собственная частота колебаний системы определяется только жесткостью спиральной пружины.
За критическую частоту датчика принимаем ее минимальное значение, полученное при расчете обоих стержней.
3.3. Динамическая погрешность суммирования сигналов
Двухконтактные приборы активного контроля значительно снижают влияние вибраций на точность измерения размеров обрабатываемых деталей. Такие приборы можно разделить на приборы с одной двухконтактной измерительной головкой, где суммирование сигналов не требуется, поскольку датчик один, и на приборы с двумя одноконтактными измерительными головками, каждая из которых имеет свой датчик, сигналы которых суммируются.
Приборы с двумя измерительными головками получили распространение, поскольку имеют сравнительно простую конструкцию самих головок, позволяют контролировать детали в большом диапазоне размеров и легко переходить от контроля размеров наружных поверхностей к контролю внутренних. Однако у этих приборов может возникнуть погрешность, которую назовем динамической погрешностью суммирования.
Для анализа динамической погрешности суммирования рассмотрим влияние вибрации в случае постоянного измеряемого размера, когда сигнал в приборе возникает только из-за вибрации его корпуса относительно измеряемой детали.
Как уже отмечалось, суммирование сигналов имеется у приборов с двумя раздельными датчиками. В этом случае при вибрации детали относительно прибора на выходе датчиков возникают одинаковые, но противоположные по знаку сигналы y1 и y2. При сложении сигналов в схеме суммирования должно иметь место
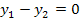 (25) (25)
что и выполняется при статической настройке приборов. В динамике равенство (25) может нарушаться, в результате чего появляется динамическая погрешность суммирования
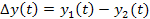 (26) (26)
В общем виде динамическую погрешность суммирования можно рассмотреть, воспользовавшись методом теории автоматического регулирования. На рис.25 изображена структурная схема прибора активного контроля с суммированием сигналов от двух датчиков. Сигналы размера детали Х1(р) и Х2(р) (оперативное изображение по Лапласу) воздействуют на датчики 2 и 3, имеющие передаточные функции W1(р) и W2(р). С выхода датчиков преобразованные сигналы
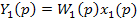
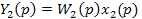
поступают на сумматор 4.
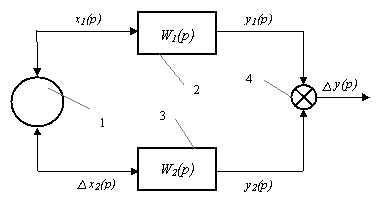
Рис.25. Структурная схема прибора с суммированием сигналов
Так как при вибрации детали (без отрыва измерительных наконечников от детали) х1 = х2 = х, то погрешность суммирования согласно уравнению (26) будет равна
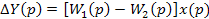 (27) (27)
Выражение (27) показывает, что динамическая погрешность суммирования зависит от разности передаточных функций звеньев, включенных до суммирования сигналов.
Проанализируем динамическую погрешность распространенной схемы суммирования, выполненной на двухапериодических звеньях, на примере электрической схемы (рис.26,а). В этой схеме элементы Ri1 и Ri2 - внутренние сопротивления источников сигнала; R1 и R2 - резисторы, на которых выполняется суммирование; C1 и С2 - элементы сглаживающего фильтра.
а)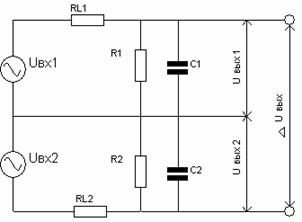
б) 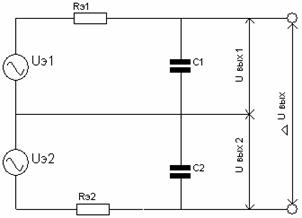
Рис 26. Схема суммирования: а – схема суммирования с двумя апериодическими звеньями; б – эквивалентная схема суммирования.
Используя представления об эквивалентном генераторе преобразуем схему в эквивалентную (рис. 26, б), где
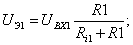 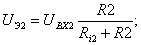
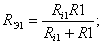 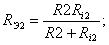
Цепи состоящие из 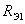 , С1 и , С1 и 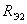 , С2 образуют апериодические звенья, передаточные функции которых соответственно равны: , С2 образуют апериодические звенья, передаточные функции которых соответственно равны:
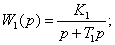 (28) (28)
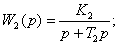 (29) (29)
где 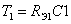 и и 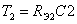 - постоянные времени; - постоянные времени;
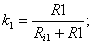 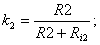 - коэффициенты передачи. - коэффициенты передачи.
Получив передаточные функции для каналов первого (28) и второго (29) датчиков на основании уравнения (27) и учитывая, что 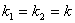 (каналы статистически согласованы), запишем выражение динамической погрешности для рассматриваемого случая: (каналы статистически согласованы), запишем выражение динамической погрешности для рассматриваемого случая:
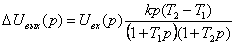 (30) (30)
Передаточную функцию погрешности можно получить из уравнения (30):
 (31) (31)
Для анализа динамики схемы суммирования используем типовое возмущение в виде гармонического возмездия.
Частотную функцию погрешности, которая выражает реакцию динамического звена на гармоническое воздействие, получим из формулы (31) путем замены оператора p на jw:
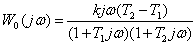 (32) (32)
Правая часть уравнения (32) представляет собой комплексное выражение, в котором умножением числителя и знаменателя на число, комплексно сопряженное знаменателю, можно выделить вещественную и мнимую части и после этого определить модуль вектора. Фаза в данном случае нас не интересует.
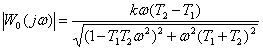 (33) (33)
Модуль вектора W0(jw) является амплитудно-частотной характеристикой и представляет собой зависимость абсолютного значения динамической погрешности суммирования от частоты вибрации при определенных параметрах схемы суммирования. На рис 27 графически изображена амплитудно - частотная характеристика при различных постоянных времени Т1 и Т2 и коэффициентов передачи k1 и k2. Значения этих величин наибольшее для кривой 1 и наименьшее для кривой 3.
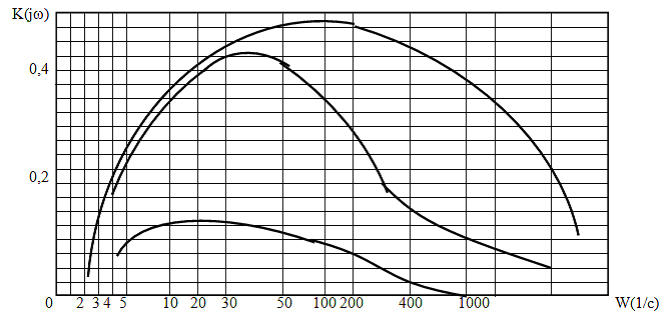
Рис. 27. Амплитудно – частотная характеристика схемы суммирования
Наиболее опасным случаем вибраций с точки зрения погрешности является скачок - ступенчатое воздействие. Принимая, что 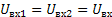 (отрыв измерительных наконечников от детали отсутствует), а k1=k2=k , напишем выражение динамической погрешности суммирования при ступенчатом воздействии: (отрыв измерительных наконечников от детали отсутствует), а k1=k2=k , напишем выражение динамической погрешности суммирования при ступенчатом воздействии:
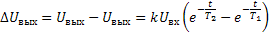 (34) (34)
Найдем максимальное значение динамической погрешности суммирования. Для этого определим время tM , за которое функция (34) достигает экстремума,
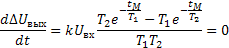
откуда
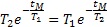
Логарифмируя и преобразуя, получим
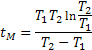
Подставляя значение tM в (34), получим максимальное значение динамической ошибки суммирования
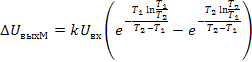 (35) (35)
На рис.28 приведена зависимость нормированной максимальной погрешности от параметров схемы.
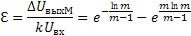
где 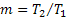
Штриховыми линиями показаны зоны возможных погрешностей при ±10%-ном (m=1,49) и при ±20%-ном (m=2,26) разбросе номинальных величин элементов схем суммирования.
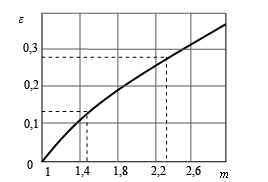
Рис.28. Зависимость нормированной максимальной погрешности от параметров схемы суммирования
Уравнения (33), (34) и (35) показывают, что величина динамической погрешности зависит от разности постоянных времен T1 и Т2. Следовательно, для уменьшения динамической погрешности требуется применять точные элементы или производить их подбор.
Рассмотренный пример возникновения динамической погрешности в схеме суммирования показывает, что качество работы систем активного контроля с суммированием сигналов характеризуется не только известными составляющими погрешности, но и так называемой динамической погрешностью суммирования. Характер данной погрешности определяется различием в каналах обоих датчиков форм переходных процессов, представляющих собой закон изменения во времени измеряемой величины вследствие измерения входного сигнала.
Как уже отмечалось выше, приборы с двумя измерительными головками позволяют контролировать детали в большом диапазоне размеров и быстро перенастраиваться с одного размера на другой, что обусловливает возможность их использования в гибких производственных системах.
С помощью этих систем, в частности, можно легко переходить от контроля наружных поверхностей к контролю внутренних. |

