.jpg)

.jpg) |
 |
|
Пример решения
На вход стационарной линейной системы Lc, описанной линейным дифференциальным уравнением с постоянными коэффициентами d3Y(t)/dt3-5d2Y(t)/dt2+12dY(t)/dt-8Y(t)=d2X(t)/dt2+X(t), подается стационарный белый шум Х(t) с характеристиками mx S*=13/2 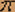 , K*x=13 , K*x=13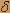 ( (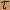 ), где ), где 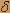 ( (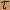 ) -дельта - функция. ) -дельта - функция. Найти характеристики случайного процесса Y(t) на выходе системы Lc. Считая Х(t) и Y(t) оригиналами с нулевыми начальными условиями, перейдем к операционному уравнению для изображений 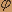 (u) и (u) и .jpg) (u); (u);(u3-5u2+12u-8) .jpg) (u)=(u2+1) (u)=(u2+1)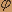 (u) (u).jpg) (u)=(u2+1)/(u3-5u2+12u-8) (u)=(u2+1)/(u3-5u2+12u-8)Следовательно, передаточная функция имеет вид G(u)=(u2+1)/(u3-5u2+12u-8)=(u2+1)/(u-1)(u2-4u+8). Частотная характеристика имеет вид G(iw)=-(1-w2)/(1+iw)(8-w2-4iw) .jpg) =(w4-2w2+1)/(w2+1)(64-16w2+w4+162)=(w4-2w2+1)/(w2+)(w4+64) =(w4-2w2+1)/(w2+1)(64-16w2+w4+162)=(w4-2w2+1)/(w2+)(w4+64) Находим my my=G(0)mx=-1/8mx Находим S*y(w)= .jpg) S*x(w)=13/2 S*x(w)=13/2 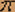 ((w4-2w2+1)/(w2+)(w4+64)) ((w4-2w2+1)/(w2+)(w4+64))Разложим рациональную дробь на простейшие (w4-2w2+1)/(w2+1)(w4+64)=A/(w2+1)+(Bw2+C)/(w4+64) w4-2w2+1=A(w4+64)+Bw2(w2+1)+C(w2+1) w4|A+B=1 w2|B+C=-2; A-C=3 w0|64A+C=1; 64A+C=1; 64A=4; A=4/65; B=61/65; C=-191/65. Следовательно S*y(w)=2/5 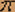 (1/w2+1)+61/10 (1/w2+1)+61/10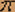 ((w2/9w4+64)-191/10 ((w2/9w4+64)-191/10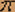 (1/w4+64) (1/w4+64)Находим Ky( 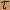 )по таблице соответствия Ky( )по таблице соответствия Ky(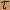 ) и S*y(w) ) и S*y(w) Ky( 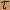 )=2/5-| )=2/5-|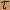 |+61/40e-2| |+61/40e-2|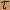 |(cos2 |(cos2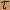 )+191/160e-2| )+191/160e-2|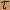 |(cos2 |(cos2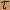 +sin2| +sin2|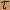 |) |)Ky( 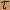 )=2/5-| )=2/5-|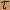 |+87/32e-2| |+87/32e-2|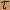 |cos2 |cos2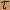 -53/160e-2| -53/160e-2|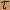 |sin2 |sin2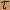
|
.jpg) |
|