.jpg)

.jpg) |
 |
|
Пример решения
Дана выборка 460213312531224443252512303051213040221051424 21310612142202422122 Объем выборки n=65 Начало первого интервала xmin=0. Длина интервала h=1. а=0,02. Требуется для выборки: а) составить вариационный ряд, б) найти частоты, относительные частоты и накопительные частоты, в) построить полигон, г) составить эмпирическую функцию распределения и построить ее график.
.jpg) .jpg)
д) найти числовые характеристики (выборочную среднюю, выборочную дисперсию, выборочное среднеквадратное отклонение) x0=( 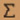 nixi)/n=(0+13+40+24+36+25+12)/65=2.31 nixi)/n=(0+13+40+24+36+25+12)/65=2.31Db=( 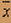 k2)b-( k2)b-(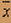 b)2=(0+13+80+72+144+125+72)/65-(2.31)2=2.45 b)2=(0+13+80+72+144+125+72)/65-(2.31)2=2.45( 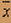 k2)b=( k2)b=(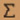 nixi)/n nixi)/n.jpg) = =.jpg) =1.57 =1.57S2=(n*/(n-1))Db=(65/64)2.45=2.48 S= .jpg) =1.57 =1.57е) найти теоретически (выравниваемые) частоты случайной величины х, в предположении, что х распределена по показательному закону, и по нормальному: n'k=(nh/ .jpg) b) b)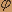 (tk) для нормального распределения (tk) для нормального распределения n'k=(nh/xb)ek-x/xb для показательного распределения где, tk=(xk-xb)/S, a 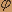 (tk) - по таблице. (tk) - по таблице.
.jpg) ж) построить теоретически кривые распределения случайных величин х и у; з) проверить гипотезы о виде распределения случайных величин х и у с заданным уровнем значимости 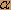
xн2= 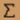 (ni-ni,)2/ni, (ni-ni,)2/ni,m=I=S-1, I=7 - количество интервалов Для показательного распределения S=1 .jpg) m=5, m=5,Для нормального распределения S=2 .jpg) m=4, m=4,Для уровня значимости .jpg) Kкр1-Kкр2=15.1-12.8=2.3 2.3/3=0.8 xпок2=25.44 Kкр.пок=13.6 x2 .jpg) 13.6 13.6Гипотеза о показательности распределения отвергается. xнор2=6.69 Kкр.нор=11.8 x2 .jpg) 11.8 11.8Гипотеза о нормальности распределения принимается.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
.jpg) |
|