.jpg)

.jpg) |
 |
|
Учебное задание Задача 1 Дана выборка А случайных величин X. Требуется а) составить вариационный ряд; б) найти частоты, относительные частоты, и накопленные частоты; в) построить полигон и гистограмму; г) составить эмпирическую функцию распределения и построить ее график; д) найти числовые характеристики (выборочную среднюю, выборочную дисперсию, выборочное среднеквадратическое отклонение); е) найти теоретические (выравниваемые) частоты случайной величины X, в предположении, что X распределена по показательному закону и по нормальному закону; ж) построить теоретические кривые распределения случайной величины X; з) проверить гипотезы о виде распределения случайных величин X с заданным уровнем значимости . Задача 2 Для элементарных случайных функций x0, x0cos2t,x0t2, где X0=X-M(X), найти характеристики и построить семейство реализаций (м(х)-выборочная средняя). Задача 3 Найти характеристики случайных функций u(t)=ae-bt, v(t)=cedxt, w(t)=fx+gt, где a, b, c, d, vf, g - неслучайные величины (смотри задание), в предположении, что X распределено по показательному закону. Задача 4 Найти характеристики случайных функций z1(t)=(a1cost+a2t2+a3t+a4et)v(t)+b1t2+b2sint+b3lnt+b4, z2(t)=(a4t2+a5sint+a2t+a1lnt)dv(t)/dt+b4et+b3t2+b2t+b1,где v(t) - элементарная случайная функция, определенная в пункте 3, a1, a2, a3, a4, b1, b2, b3, b4-неслучайные величины из задания. Задача 5 Найти характеристики случайных функций Z4(t)=(a1eat+a2lg(bt)+a3tc+a4ln(dt)) 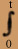 u(s)ds+b1Int+b2t3+b3sint+b4, где u(t) - элементарная случайная функция, определенная в пункте 3, a, b, c, d- неслучайные величины из таблицы 1, a1, a2, a3, a4,
b1, b2, b3, b4-неслучайные величины из задания.
u(s)ds+b1Int+b2t3+b3sint+b4, где u(t) - элементарная случайная функция, определенная в пункте 3, a, b, c, d- неслучайные величины из таблицы 1, a1, a2, a3, a4,
b1, b2, b3, b4-неслучайные величины из задания.
Задача 6 На вход стационарной линейной системы , Lc, описанной линейным дифференциальным уравнением с постоянными коэффициентами a3d3/dt3y(t)+a2d2/dt2y(t)+a1d/dty(t)+a0y(t)=b2d2/dt2x(t)+b1d/dtx(t)+b0x(t), подается стационарный белый шум x(t) с характеристиками mx, Sx(u)=c/2 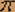 ,
Kx( ,
Kx(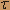 )=c )=c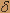 ( (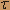 ), где ), где 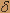 ( (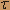 ) - дельта-функция. ) - дельта-функция. Найти характеристики случайного процесса y(t) на выходе системы Lc.Коэффициенты линейного дифференциального уравнения приведены в таблице 3.
|
.jpg) |
|