( 7.1 ) Как было упомянуто ранее, одним из показателей работы САУ является ее способность возвращаться в исходное состояние после воздействия какого - то возмущения.
Под действием некоторого возмущения выходная величина (управляемая величина) отклоняется от заданного значения. Если вели- чина этого отклонения увеличивается со временем, то система является неустойчивой. Для устойчивой системы характерно уменьшение этого отклонения со временем.
В настоящее время разработаны методы оценки устойчивости системы, позволяющие дать ее оценку, не решая дифференциальных уравнений, а основываясь на их коэффициентах. Наиболее распространенными в настоящее время являются следующие критерии: Гурвица, А.В. Михайлова и Найквиста.
7.1. Необходимое и достаточное условия устойчивости
С математической точки зрения переходный процесс представляет собой общее решение дифференциального уравнения, описывающего поведение САР.
( 7.1 )
Общее решение находим на основе решения характеристического уравнения САУ.
а 0 р n + . . . +а n = 0 ( 7.2 )
Если все корни этого уравнения простые ( это не влияет на общ- ность наших рассуждений ) , то переходной процесс будет выражен так:
где С 1 , С 2 , ... , С n - произвольные постоянные.
Для устойчивости САУ необходимо, чтобы переходные процессы, вызванные теми или иными внешними воздействиями, со временем затухали, т.е.
( 7.3 )
Т.к. коэффициенты уравнения (6.15) вещественные, то его корни могут быть либо вещественными, либо комплексно сопряженными. .
Для вещественных корней р k = a k
( 7.4 )
Для комплексно сопряженных корней р к , к + 1 = a к ± j w к ,
( 7.5 )
Так как вещественные корни являются частным случаем комплексных корней, то из выражений (7.3) , (7.4) и (7.5) можно вывести необходимое и достаточное условие устойчивости линейных систем.
Для устойчивости линейной САУ необходимо и достаточно, чтобы вещественные части всех корней характеристического уравнения САУ были отрицательны, т.е. чтобы
(7.6)
Другими словами все корни характеристического уравнения должны быть расположены в левой полуплоскости графика (рис. 7.1, а ).
Рис.7.1. Расположение корней характеристического уравнения САР пятого порядка: а - для устойчивой САР; б - для неустойчивой САР.
Если хотя бы один корень или пара корней находятся в правой полуплоскости ( рис. 7.1, б ) , то САР будет неустойчивой.
Возможен случай, когда хотя бы один вещественный корень или пара комплексных корней находятся на мнимой оси ( a к = 0), а остальные - в левой полуплоскости, то это соответствует границе устойчивости (рис. 7.2).
Рис. 7.2. Расположение корней характеристического уравнения САУ на границе устойчивости: а - апериодическая устойчивость; б- колебательная устойчивость
Из условия (7.6) можно сформулировать необходимое условие устойчивости САУ, которое часто используется на практике. Оно формулируется так: для устойчивости линейной САУ необходимо, чтобы все коэффициенты характеристического уравнения (7.6) были положительными, т.е.
a к > 0 , k = 1, 2, ... , n ( 7.7 )
7.2. Критерии оценки устойчивости САУ
Полученное условие (7.6) с математической точки зрения означает, что исследование устойчивости САР сводится к задаче определения знаков действительных частей корней характеристического уравнения. Эту процедуру можно осуществить, совсем не решая уравнения, так как для уравнений высоких порядков это является достаточно трудоемкой задачей и на практике неприемлемо. Причем, такой подход совсем не годится при исследованиях, связанных с вариацией величин этих коэффициентов.
Поэтому в теории разработаны методы исследования устойчивости САР, совершенно не требующие определения корней характеристического уравнения. Эти методы получили название критериев устойчивости.
Широко распространены три критерия устойчивости: алгебраический метод Гурвица и два частотных - Михайлова и Найквитса. Каждый из них имеет свою более или менее определенную область применения.
7.2.1 Критерий устойчивости Гурвица
Данный критерий формулируется следующим образом.
Если характеристическое уравнение замкнутой системы имеет вид (7.2 ) и а 0 > 0 , то для устойчивости линейной САУ необходимо и дос- таточно, чтобы были положительны n определителей Гурвица D 1 , D 2 , ... , D n , т.е. выполнялась система неравенств
D k > 0 , k = 1, 2, ... , n ( 7.8 )
Эти n определителей представляют собою диагональные определители квадратной матрицы n -го порядка, составленной из коэффициентов уравнения ( 7.2 ) и имеющей вид:
( 7.9 ),
тогда имеем:
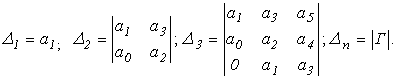(7.10 )
Несложно убедиться, что D n = a n ? D n - 1 . Поэтому условие D n > 0 разделяется на два условия: а n > 0 и D n - 1 > 0 и вычислять последний определитель D n не нужно.
Следует заметить, что условие D n - 1 = 0 является необходимым и достаточным условием наличия пары чисто мнимых корней ± j w 0 в уравнении (7.2) . В этом случае САР находится на границе колебательной устойчивости или может быть неустойчивой. Все зависит от взаимного рас-положения корней относительно оси j w . Условие нахождения САУ на границе колебательной устойчивости по критерию Гурвица имеет вид:
D 1 > 0 ; D 2 > 0; . . . ; D n - 2 > 0; D n - 1 = 0 ( 7.11 )
Данный метод из-за своей громоздкости не применяется для систем выше 5 го порядка.
В таблице 1 приведены условия устойчивости по критерию Гурвица для систем от 1 го до 5 го порядков.
Таблица7.1.
Условия устойчивости по Гурвицу
Порядок уравнения |
Условия устойчивости |
1 |
а 0 > 0; a 1 > 0 |
2 |
a 0 > 0; a 1 > 0; a 2 > 0 |
3 |
a 0 > 0; a 1 > 0; a 2 > 0; a 3 > 0; a 1 a 2 > a 0 a 3 |
4 |
a 0 > 0; a 1 > 0; a 2 > 0; a 3 > 0; a 4 > 0; a 3 ( a 1 a 2 - a 0 a 3 ) - a 2 1 a 4 > 0 |
5 |
a 0 > 0; a 1 > 0; a 2 > 0; a 3 > 0; a 4 > 0; a 5 > 0; a 1 a 2 > a 0 a 3 ; ( a 1 a 2 - a 0 a 3 ) ( a 3 a 4 - a 2 a 5 ) > ( a 1 a 4 - a 0 a 5 ) 2 . |
7.2.2. Критерий устойчивости Михайлова
Критерий устойчивости Михайлова позволяет судить об устойчивости САУ по кривой Михайлова - годографу вектора D(j w ):
D( j w ) = D( p) | p = j w = a n ( j w ) n + . . . + a 0 , ( 7.12 )
что и представляет собой полином замкнутой системы.
Годографом этого вектора будет некоторая кривая на плоскости [ X ( w ), jY ( w )] при изменении w от нуля до бесконечности.
В правой части выражения (7.12) выделим действительную и мнимую составляющие и получим
D( j w ) = X( w ) + jY( w ), ( 7.13 )
где
X( w ) = Re D( j w ) = a n - a n - 2 w 2 + a n - 4 w 4 - ...
( 7.14 )
Y( w ) = I m D( j w ) = a n - 1 w - a n - 3 w 3 + a n - 5 w 5 ...
Кривую Михайлова строят по точкам в плоскости [ X( w ); jY( w ) ] согласно (7.13), причем каждой точке соответствует свое значение w . Направление возрастания w на кривой указывается стрелкой.
По критерию Михайлова для устойчивой системы необходимо и достаточно, чтобы при изменении угловой частоты от 0 до ? годограф, описываемый концом вектора D(j w ), начинался на вещественной поло- жительной полуоси и, вращаясь только против часовой стрелки, нигде не обращался в нуль, проходил, повернувшись на угол j = n p / 2, последо- вательно число квадрантов, равное степени n характеристического урав- нения ( 7.2 ).
На рис. 7.3 представлены годографы Михайлова для различных систем.
7.2.3. Критерий устойчивости Найквиста.
Используя критерий устойчивости Найквиста, устойчивость замкнутой системы автоматического регулирования определяют по час- тотным характеристикам разомкнутой системы. Для этого обычно используют АФХ или ЛАЧХ разомкнутой системы.
АФХ разомкнутой системы получают следующим образом. Нужно разорвать цепь внешней обратной связи системы на структурной схеме и проанализировать динамические звенья, входящие в главный контур. Если главный контур системы не имеет неустойчивых звеньев и содержит не более одного интегрирующего звена, то можно применять этот критерий. По структурной схеме разомкнутой устойчивой системы определяют передаточную функцию разомкнутой системы W раз ( р) . Вместо оператора р подставляем j w и получаем уравнение АФХ разомкнутой системы. Правую часть этого уравнения представляем в виде:
W раз ( j w ) = X( w ) + jY( w ). ( 7.15 )
Изменяя частоту w от 0 до ? , получаем пары значений X( w ) и Y( w ) , по которым на комплексной плоскости [ X ( w ); jY( w ) ] строим АФХ разомкнутой системы.
Если эта характеристика не охватывает точку с координатами (-1; j0), то замкнутая система устойчива. На рис. 7.4 представлены АФХ устойчивых и неустойчивых систем ( статической и астатической ).
7.2.4. Определение областей устойчивости
Рассмотренные ранее характеристики определения устойчивости позволяют определить устойчива ли система при определенных значениях параметров и практически мало пригодны, чтобы дать ответ на вопрос об устойчивости системы при их изменениях в некоторых пределах. На этот вопрос дает ответ так называемый метод D - разбиений. Метод D – разбиений достаточно трудоемкий, а поэтому мы рассмотрим простой случай: метод D - разбиения по одному комплексному параметру на примере некоторой астатической системы автоматического регулирования, кото- рая описывается уравнением 4 го порядка:
( 7.16 )
где y ( t) - выходная величина; x ( t) - входная величина; k - коэффициент усиления.
Характеристическое уравнение уравнения (7.2) имеет вид
а 0 р 4 + а 1 р 3 + а 2 р 2 + а 3 р + k = 0 ( 7.17 )
Допустим, что в уравнении (7.17) нам известны все коэффициенты a 0, а 1 , а 2 , а 3 , а коэффициент усиления k неизвестен. Положим, что при некотором значении коэффициента усиления k два корня характеристического уравнения находятся в левой полуплоскости комплексной плоскости, а два - в правой полуплоскости. Из этого следует, что система неустойчива (два корня имеют положительные действительные части). Поскольку коэффициенты алгебраического уравнения и значения корней связаны между собой, то, изменяя величину коэффициента усиления k , можно корни, находящиеся в правой полуплоскости, перевести ближе к мнимой оси, поместить на ось или даже в другую полуплоскость. Корни же, находящиеся в левой полуплоскости, могут при определенных условиях там и находиться. В этом случае система станет устойчивой.
На комплексной плоскости коэффициента усиления k можно выделить область его значений, при которых система будет устойчивой. Эта область и будет областью устойчивости. Другими словами - при значениях коэффициента k внутри этой области система будет устойчивой, а вне ее - неустойчивой.
Границей области устойчивости являются значения коэффициента усиления k , при которых хотя бы один корень расположен на мнимой оси. Таким образом , за границу устойчивости принимаем отображение мнимой оси комплексной плоскости корней характеристического уравнения на комплексной плоскости коэффициента усиления k . Подобным образом мы можем действовать в отношении любого из коэффициентов характеристического уравнения, но удобнее и нагляднее пользоваться конкретными параметрами - постоянными времени, коэффициентами усиления, которые линейно входят в уравнение и их легко можно изменять.
Положим, что в данном уравнении (7.17) мы имеем три коэффициента усиления k = k 1 ? k 2 ? k 3 , тогда, сделав замену р = j w и разделив действительную и мнимую части, получаем:
( 7.18 )
Пусть коэффициент k 1 нам неизвестен, т.е. k 1 = k x . Определим его из уравнения (7.18):
( 7.19 )
Изменяя теперь w от - ? до + ? , получим значения k x для всех возможных корней, которые располагаются на мнимой оси. Значений оставшихся трех корней мы не знаем для каждого вычисления k x при w = const. Вычислив для различных w пары значений действительной X ( w ) и мнимой Y( w ) частей, строим на комплексной плоскости параметра k x кривую, которая будет отображением мнимой оси комплексной плоскости корней характеристического уравнения (рис. 7.5)
В устойчивой системе автоматического управления все корни характеристического уравнения находятся слева от мнимой оси. При изменении w от - ? до + ? область устойчивости также будет расположена слева от полученной кривой. Для удобства определения области устой- чивости наносят на кривую штриховку слева при изменении w от - ? до + ? .
На практике задаются значе- нием k x = k 1 , лежащем внутри заштрихованной области, определяют коэффициент усиления k = k 1 ? k 2 ? k 3 . После этого подставляют значение k в уравнение (7.17) и с помощью любого из критериев устойчивости проверяют устойчивость системы. Если система будет устойчива, то данная область является областью устойчивости. Такая проверка необходима, так как при определенном значении k x , находящемся на границе области устойчивости, помимо корней с отрицательной действительной частью могут быть корни с положительной действительной частью. Иными словами, может получиться так, что область устойчивости будет отсутствовать, при любом значении k x или другого рассматриваемого параметра. В этом случае система автоматического управления называется структурнонеустойчивой, и для достижения устойчивости нужно изменить структурную схему.
7.3. Оценка качества процесса регулирования
Ответ на вопрос устойчива или неустойчива САУ говорит о том, что с течением времени переходной процесс затухает и система приходит в устойчивое состояние после того, как она испытала какое - то воздействие. Устойчивость работы САУ является только необходимым, но далеко не достаточным условием практической пригодности САУ. Помимо устойчивости в работе САУ должна обеспечивать необходимую точность работы.
Качество САУ определяет точность ее работы в установившемся и переходном режимах. На рис.7.6 даны примеры переходных характеристик САУ, представляющих переходные процессы в системах, вызванные единичным воздействием. Для оценки качества САУ по виду переходных характеристик вводят следующие показатели качества: время переходного процесса t п , максимальное отклонение в переходный период s , колебательнлсть переходного процесса М.
Время переходного процесса t n . Этот показатель характеризует быстродействие системы. Время переходного процесса t n равно интервалу времени от начала переходного процесса до момента, когда выходная величина достигает 95% ее нового установившегося значения.
Максимальное отклонение в переходный период (перерегулирование) s . В случае переходного процесса, вызванного возмущением F (см.рис.7.6), максимальное отклонение определяется величиной y 1 max . В случае переходных процессов, вызванных изменением задающего воздействия х з , максимальное отклонение выражается в процентах и определяется следующим образом:
( 7.20 )
Эта величина часто называется перерегулированием. Допусти- мым считается s < ( 10 ... 30 ) %.
Колебательность переходного процесса М. Колебательность М определяется числом колебаний, равным числу минимумов кривой переходного процесса за время переходного процесса t n ( рис. 7.6 ) или в случае кривых ( рис. 7.6, б ) - числом перерегулирований за тот же период.
В некоторых случаях колебательность определяют как отношение соседних максимумов, например: y 2 max / y 1 max , выраженное в процентах. Приемлемым числом колебаний считается 1…2.
В процессе синтеза САУ при составлении ее структурной схемы и выборе значений параметров выполнение перечисленных выше требований заставляет нас идти на компромисс. Например, в ряде случаев с увели- чением коэффициента усиления будет увеличиваться быстродействие, но и увеличиваться колебательность.
Кроме того, характер переходного процесса будет зависеть от места приложения и вида воздействия, а также от начальных условий.
Другими словами, при оценке качества переходных процессов необходимо указывать воздействие и начальные условия, при которых имеет место данное качество. При общей характеристике качества переходных процессов в САУ за стандартное воздействие обычно принимают единичное ступенчатое воздействие при нулевых начальных условиях, что позволяет получать переходную характеристику.
Существуют три группы методов оценки качества переходных процессов. Первая – корневые – по значениям полюсов и нулей передаточной функции системы, (т.е. по корням её числителя и знаменателя). Вторая – частотные – по частотным характеристикам системы и третья – интегральные – по характеру интегральной кривой процесса.
Каждый из методов оценки качества переходных процессов имеет свои преимущества и недостатки. Наиболее приемлемыми являются частотные методы, а среди них метод оценки запаса устойчивости и быстродействия САУ по вещественной частотной характеристике замкнутой системы.
Оценка запаса устойчивости и быстродействия САУ по вещественной частотной характеристике. Для проведения этой оценки воспользуемся этой характеристикой замкнутой САУ Ф гл ( j w ) , которая может быть получена путём формальной замены р на j w , т.е. переходом от единичного ступенчатого воздействия к гармоническому, и запишем
При экспериментальном снятии характеристик для каждого значения частоты гармонического воздействия определяют амплитуду выходной величины, а также фазовый сдвиг между выходным и входным сигналами. Следует отметить, что переходный процесс и вещественная частотная характеристика связаны между собой.
Эта связь математически выражается так:
. (7.23)
При единичном входном воздействии выходной сигнал y ( t ) будет представлять собой переходную характеристику h ( t ).
На основе (7.23) можно оценить границы переходного процесса по амплитуде и длительности, определить его начальные и конечные значения, оценить перерегулирование.
На практике используют следующие правила для косвенной оценки качества САУ (рис.7.7).
1.Кривая переходного процесса ограничена по модулю, если Р( w ограничена по модулю на всём диапазоне рабочих частот.
2.Чем больше пик графика вещественной частотной характеристики Р( w), тем больше колебательность переходного процесса (см.рис.7.7,а).
3.Чем плавней график Р(w), тем быстрее затухает переходный процесс (см.рис.7.7,б,в, рис.7.7,г-резонанс).
На рис.7.7 даны типовые графики частотных вещественных характеристик Р( w) замкнутых САУ.
4.Начальное значение вещественной характеристик Р( 0 ) равно установившемуся значению переходной функции
P(0) = h у с т = y у с т (7.24)
при входном единичном воздействии.
Для определения h уст в формулу (5.14) подставим выражения (5.5), (5.6) и получим
Отсюда следует, что 
для статических САУ и Р( 0 )= 1 для астатических.
5.При единичном ступенчатом воздействии на САУ время переходного процесса удовлетворяет неравенству
, (7.26),
где w п – диапазон частот, в котором Р ( w ) >0. На графике указана частота w с . Это так называемая граничная частота диапазона существенных частот. Амплитуды с частотами больше, чем w с пренебрежимо малы.
6. Для определения величины перерегулирования 
используют выражение
. (7.27)
Здесь следует отметить, что чем ближе система подходит к колебательной границе устойчивости, тем выше пик (рис. 7.7, а ), а при резонансе Р ( w ) терпит разрыв на резонансной частоте w о .
7. Для системы, имеющей вещественную частотную характеристику (рис.7.7, б ) – положительную, убывающую ( в диапазоне частот 0 
выполняются условия Р ( w ) > 0 и 
, перерегулирование 
, время переходного процесса удовлетворяет неравенству
(7.28)
0 ? w ? w с
8. Для системы, имеющей вещественную частотную характеристику вида на рис.7.7, в ( в диапазоне частот ) выполняютсяусловия Р ( w ) >0 и 
, перерегулирование 
и выходная величина изменяется плавно.
Из выражений (7.26) и (7.27) следует вывод, что при использовании вещественной частотной характеристики Р ( w) для оценки качества САУ быстродействие САУ определяется интервалом частот 
, на котором Р ( w )>0, а запас устойчивости – ординатой Р max .
Недостатком этого метода следует отметить трудоемкость построения вещественной характеристики Р ( w ) для систем высоких порядков, а также использование косвенных критериев качества и Р max , что в общих случаях приводит к сложным выражениям через параметры системы.
Наличие же прямой связи между косвенными критериями и Р max и прямыми критериями t n и является его преимуществом.
Существуют и другие методы оценки качества, обладающие своими преимуществами и недостатками. При необходимости с ними можно познакомиться в существующей специальной литературе.
Очень часто при разработке и реконструкции работающих САУ проводят операцию анализа САУ, т.е. составляют схему, определяют качественные показатели и соответствие их техническим требованиям. Чтобы изменить какие-либо параметры в схему вносят коррективы и вновь проводят анализ. Это может повторяться несколько раз, что весьма неудобно. Поэтому основным способом решения таких задач является синтез САУ, в основе которого лежит весь аппарат теории автоматического управления. Задача синтеза заключается в создании САУ в виде ее математического описания для данного объекта управления при опреде- ленных условиях работы, характеристиках внешних воздействий и обеспечении на основе полученной математической модели требований к надежности, весу, габаритам, потребляемой мощности и другим параметрам.
При решении этой задачи нельзя наилучшим образом удовлетво- рить всем требованиям, обеспечить максимальные значения всех параметров. Практически это сделать невозможно, но максимально удовлетворить главным требованиям можно. На практике в существующую САУ вводят так называемые корректирующие элементы, чтобы получить желаемые показатели работы САУ.
В настоящее время существует целый ряд методов анализа и синтеза САУ, имеющих свою специфику, преимущества и недостатки и применяемых в том или ином конкретном случае.
Наиболее широко распространён в инженерной практике синтез корректирующих устройств методом ЛАЧХ. Сущность этого метода заключается в следующем.
Представим САУ (рис.7.8) как состоящую из двух частей: основной части с передаточной функцией W 1 ( p ) и вводимой нами корректирующей части с передаточной функцией W к ( p ).
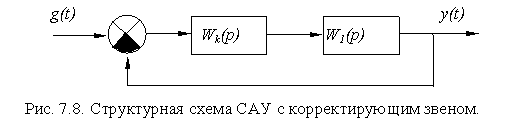
Для данной структурной схемы передаточная функция разомкнутой синтезируемой системы будет иметь вид:
W c ( p ) = W k ( p ) W 1 ( p ) , (7.29)
а выражения для логарифмических амплитудной и фазовой частотных характеристик запишутся:
L c ( w )=20lg o W c (j w ) o =20lg o W k (j w ) o +20 lg o W 1 (j w ) o , (7.30)
(7.31)
где
- ЛАЧХ корректирующего контура;
- ЛАЧХ основной (исходной) системы;
- ФЧХ корректирующего контура;
- ФЧХ основной исходной системы.
Так как логарифмические амплитудные характеристики основной (исходной) системы 
и скорректированной (той, которую нам нужно иметь) 
известны, то из выражения (7.30) находим логарифмическую характеристику корректирующего контура
. (7.32)
Построение L 1 ( w ), производят по ее передаточной функции W 1 ( p ) рис.7.9.
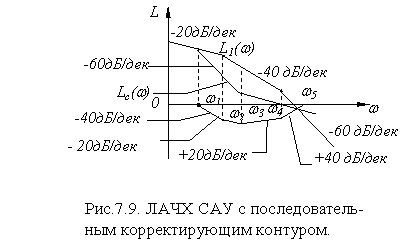
Значительные по протяженности отрезки ЛАЧХ заменяют прямыми линиями – асимптотами по отношению к реальной характеристике, что не оказывает большого влияния на точность получаемого результата. Их располагают таким образом, чтобы они имели положительный или отрицательный наклоны, на практике кратные 20 дБ/дек (0 дБ/дек, 20 дБ/дек, 40 дБ/дек и т. д.).
ЛАЧХ синтезированной системы L c ( w ) обычно делят на три части: низкочастотную, среднечастотную и высокочастотную.
Рассмотрим каждую из них в отдельности.
Низкочастотная часть ЛАЧХ характеризует точность работы САУ в установившемся режиме. Низкочастотная составляющая L c ( w ) может быть низкочастотной составляющей L 1 ( w ), если основная часть САУ имеет динамические звенья, обеспечивающие требуемые статические параметры.
Среднечастотная часть является наиболее важной частью ЛАЧХ, т.к. она определяет устойчивость и качество работы САУ в динамическом режиме. Ее основные параметры: наклон и частота среза w ср , на которой искомая ЛАЧХ ( т.е. ЛАЧХ синтезированной системы) пересекает ось частот. Наиболее целесообразно иметь наклон 20 дБ/дек , т.к. при больших наклонах очень трудно получить хорошие динамические свойства системы. Величина частоты среза w ср определяет быстродействие САУ в прямо пропорциональной зависимости.
Высокочастотная часть ЛАЧХ не оказывает существенного влияния на работу САУ и поэтому для уменьшения влияния высокочастотных помех ее наклон делают максимально большим. В некоторых слу- чаях ее можно просто не учитывать.
При построении ЛАЧХ синтезированной САУ низкочастотную и среднечастотную части ЛАЧХ соединяют между собой сопрягающими асимптотами с наклонами от 40 до 60 дБ/дек . На рис.7.9 дано построение ЛАЧХ синтезированной САУ с учетом приведенных выше соображений.
Величины сопрягающих частот w 1 … w 5 определяются по точкам пересечения асимптот. Разность L c ( w ) и L 1 ( w ) согласно (7.32) дает L к ( w ). При построении желательно, чтобы вид требуемой ЛАЧХ L c ( w ) как можно меньше отличался от вида исходной ЛАЧХ L 1 ( w ) .
По полученной ЛАЧХ L к ( w ) составляют передаточную функцию W k ( p ) на основании следующего правила. Если на сопрягающей частоте .
w i происходит изменение наклона на n 20 дБ/дек, то в передаточную функцию W k ( p ) нужно ввести множитель 
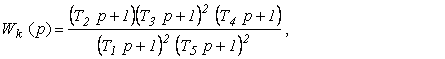(7.33)
При увеличении наклона (- n 20 дБ/дек ) этот множитель входит в знаменатель W k ( p ) , а при уменьшении (+ n 20 дБ/дек ) – в ее числитель. По полученной на рис.7.9 ЛАЧХ запишем выражение для передаточной функции корректирующего контура где 
По полученной передаточной функции W k ( p ) корректирующего контура выбирают схему контура, а потом параметры элементов по специальным таблицам. Проверку производят построением переходного процесса синтезированной системы.
<Назад> |