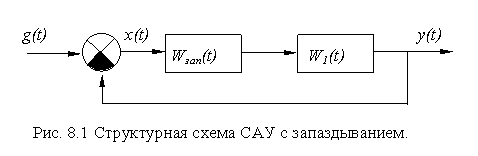
8.1 Системы автоматического управления с запаздыванием
Практически все САУ являются системами, обладающими тем или иным запаздыванием, определяемым, как правило, параметрами объекта.
На структурных схемах этот факт отображается наличием звена запаздывания (рис.8.1).
Звено запаздывания с передаточной функцией W зап ( р ) включено последовательно с основной частью САУ, не имеющей запаздывания. На этом основании мы можем записать уравнение разомкнутой САУ с запаздыванием
(8.1)
где 
t - постоянная запаздывания; W 1 ( p ) – передаточная функция основной части (без запаздывания).
Исследовать устойчивость этих САУ возможно, используя различные методы. Продемонстрируем это с помощью метода Найквиста, так как процедура относительно проста.
В выражении (8.1) сделаем формальную замену p = j w и получим уравнение АФЧХ разомкнутой САУ с запаздыванием
(8.2)
Представим теперь W 1 ( j w ) в показательной форме записи
W(j w )=A 1 ( w ) e j j 1 ( w ) ? e - j w t =A 1 ( w )e j[ j ( w ) - w t ] (8.3)
где A 1 ( w ) = 
- модуль W 1 ( j w ), j 1 ( w ) – аргумент W 1 ( j w ).
Из анализа (8.3) видно, что данное выражение от соответствующего выражения для C АУ без запаздывания отличается наличием множителя 
, что соответствует дополнительному повороту вектора передаточной функции САУ без запаздывания на угол w t по часовой стрелке на каждой частоте.
Проиллюстрируем это рис. 8.2.
Кривая 1 представляет собой АФЧХ системы без запаздывания. Зададимся некоторой частотой w 1 и проведем радиус-вектор ОА, лежащий на прямой ON . Далее определим угол t w 1 и повернем линию ON на этот угол по часовой стрелке в положение ON 1 и на пересечении дуги радиуса ОА с прямой ON 1 получим точку А 1 радиус - вектора ОА 1 искомой
АФЧХ на частоте w 1 . В результате, дейст- вуя подобным образом, получим все точки АФЧХ САУ с запаздыванием (кривая 2). Если эта кривая не охватывает точку с координатами (-1; j 0 ) на комплексной плоскости , то система будет устойчивой.
К нелинейным САУ относятся те системы, которые содержат в своей структуре нелинейные элементы. В этом случае динамика процессов описывается нелинейными дифференциальными уравнениями, решение которых представляет собой отнюдь не легкую задачу. Следует сразу отметить такую особенность нелинейных САУ – в некоторых случаях они устойчивы при малых отклонениях и неустойчивы при больших.
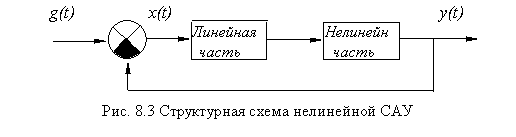
Обычно в нелинейной САУ выделяют две части – линейную и нелинейную(рис.8.3).
В настоящее время для исследования переходных процессов в нелинейных САУ используют метод фазовой плоскости. Этот метод позволяет получить качественное представление о переходном процессе в нелинейной САУ (рис. 8.4).
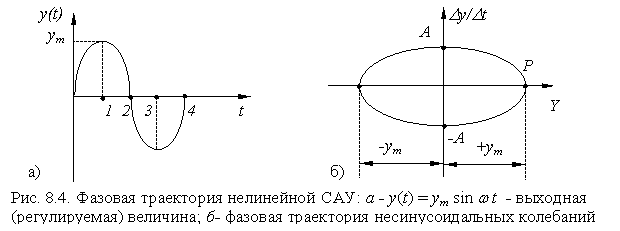
При построении фазовых траекторий берут такую систему координат: отклонение выходной (регулируемой) величины Y = D y – по оси абсцисс, а скорость этого отклонения Y ? - по оси ординат.
В нашем случае регулируемая величина y ( t ) изменяется по гармоническому закону с некоторым периодом Т и амплитудой y m . Если отклонение регулируемой величины Y = D y изменяется по синусоидальному закону от нуля до 
y m , а производная Y ? при соответствующих значениях аргумента – от нуля в точках 1 и 3 до некоторого максимального зна- чения в точках 2 и 4, меняя знак в соответствии с кривой переходного процесса, то на графике 
мы получим эллипс, на котором точка Р будет перемещаться по часовой стрелке. Очевидно, при изменении амплитуды колебаний выходной величины y m происходит изменение размеров эллипса. По полученной на фазовой плоскости кривой судят о характере изменения выходной (регулируемой) величины. Если мы получаем на фазовой плоскости замкнутый контур, то регулируемая величина совершает колебания с амплитудой y m и процесс является устойчивым.
Таким образом, построив фазовые траектории, можно делать вывод о том, какие переходные процессы возможны в данной нелинейной САУ. На рис.8.5 дано несколько примеров фазовых траекторий.
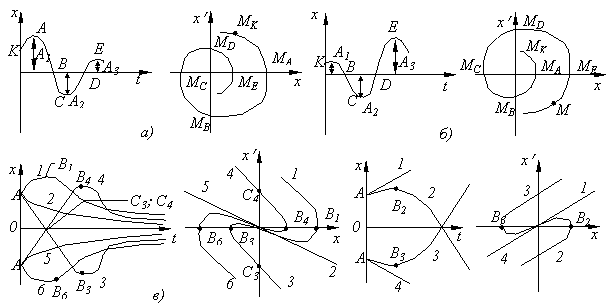
Рис. 8.5. Фазовые траектории различных переходных процессов нелинейных систем: а -колебательный затухающий; б - колебательный расходящийся; в - апериодические затухающие; г - апериодические расходящиеся.
В приведенных на рис.8.5 случаях полагают, что движение точки по фазовой плоскости описывается одним уравнением, но в некоторых случаях (например, при наличии релейного элемента) этого сделать нельзя. Это в случае, когда поведение системы на разных участках описывается двумя или тремя дифференциальными уравнениями, что приводит к двум или трем уравнениям, описывающим движение точки по фазовой плоскости.
В релейных САУ обязательно наличие релейного элемента, что приводит к переходу от непрерывных сигналов к дискретным. Дискретный сигнал изменяется во времени скачками. В большинстве дискретных САУ существуют как непрерывные, так и дискретные сигналы, что обуславливает необходимость существования устройств, преобразующих непрерывный сигнал в дискретный и наоборот – из дискретного в непрерывный.
Преобразование непрерывного (аналового) сигнала в дискретный (импульсный) называется квантованием. Известны два вида квантования: по уровню и времени (рис.8.6).
При квантовании по уровню сигнал принимает только вполне определенные дискретные значения, соответствующие уровням, показанным на рис. 8.6, б горизонтальными линиями с шагом D y . При квантовании по времени сигнал изменяется скачком в фиксированные моменты времени, показанные вертикальными линиями с шагом D t .
В соответствии с указанными видами квантования дискретные САУ делятся на три типа: релейные (это всегда нелинейные САУ) с квантованием по уровню; импульсные (это линейные САУ) с квантованием по времени; цифровые (нелинейные) со смешанным квантованием.
В релейных САУ квантование по уровню осуществляют релейные элементы, статические характеристики которых представлены на рис. 8.7.
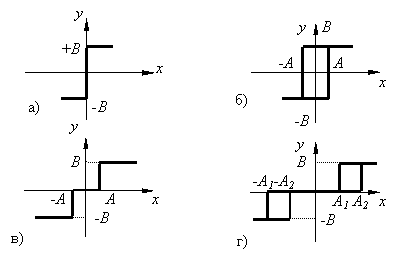
Рис. 8.7. Статические характеристики релейных элементов.
а - идеальное двухпозиционное реле:
б- двухпозиционное реле с зоной нечувствительности:
в- идеальное трехпозиционное реле:
г- трехпозиционное реле с зонами нечувствительности:
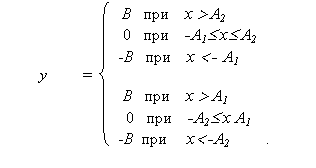
Функционально релейный элемент может входить в состав любого звена устройства управления или объекта.
Релейные системы достаточно просты, т.к. устройства релейного действия обычно проще устройств непрерывного пропорционального действия. Кроме того, они экономичны, надежны, и обладают хорошим быстродействием. В релейных САУ нашли применение двух и трёхпозиционные САУ. В качестве технического примера двухпозиционного регулятора можно привести терморегулятор электрического утюга, в котором термореле ( биметаллическая пластинка ) включает и выключает ток в термоэлементе, поддерживая тем самым заданную температуру. На рис. 8.8 представлена типовая статическая характеристика двухпозиционного релейного элемента такой системы и характер установившегося процесса.
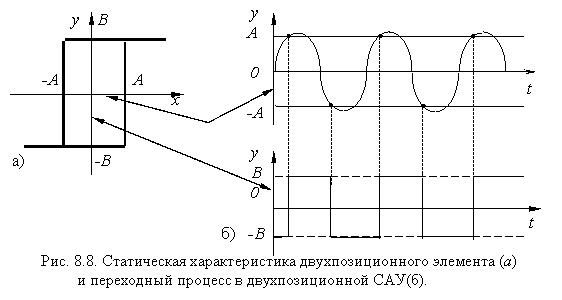
В системе переходный процесс сводится к изменению времени включения и выключения системы. С течением времени устанавливается постоянная скважность импульсов тока в термоэлементе ( отношение периода к длительности импульса).
Для двухпозиционных САУ характерны следующие особенности:
1 - отсутствие статического режима и единственным возможным невозмущённым режимом являются автоколебания, а точность САУ определяется средним значением выходной величины и амплитудой колебаний;
2 - при достаточно высокой частоте переключений достигается режим вибрационной линеаризации, т.е. система ведет себя как непрерывная и возможно повысить ее точность.
Для трёхпозиционных САУ характерно наличие релейных элементов со статическими характеристиками рис. 8.7 в,г , имеющими зону нечувствительности. В этих системах в принципе возможен статический режим покоя без автоколебаний, когда входная величина релейного элемента х ( t ) находится в зоне нечувствительности и поэтому выходная величина у ( t ) = 0.
Исследование релейных САУ ведется по тому же алгоритму, что и для непрерывных САУ: математическое описание системы, исследова- ние точности, устойчивости, качества переходных процессов и построе- ние переходных процессов. Однако эти вопросы выходят за рамки программы обычного курса и здесь поэтому не рассматриваются.
Импульсными системами называются системы, в которых сигналы квантованы по времени. На рис. 8.9 показано такое преобразование непрерывного сигнала в импульсный.
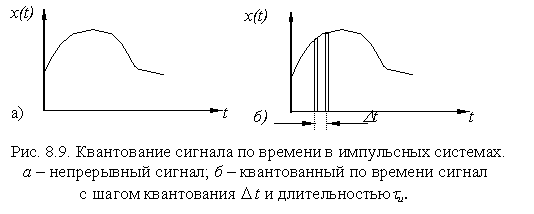
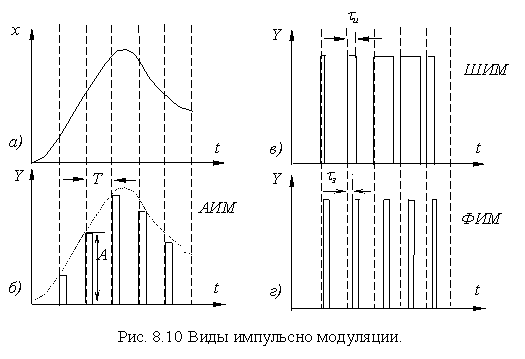
На входе системы имеется непрерывный сигнал (рис.8.9, а ) (часто медленно изменяющийся), который преобразуется в последовательность импульсов длительностью t и и периодом D t. Этот дискретный сигнал проходит через все звенья САУ, а на выходе вновь преобразуется в непрерывный. Такое преобразование называется импульсной модуляцией. Модулируемым параметром для последовательности импульсов на выходе импульсного элемента может быть высота или амплитуда импульсов, их длительность и период повторения. В зависимости от этого различают три вида модуляции. На рис. 8.10 представлены эти виды модуляции :
а - исходный сигнал, модулирующий;
б - АИМ- амплитудно-импульсная модуляция. Амплитуда им- пульса U m . зависит от значения исходного сигнала в момент квантования, Т-период.
в -ШИМ- широтно-импульсная модуляция. Ширина (длительность) импульса зависит от значения исходного сигнала в момент кван- тования, t и - ширина импульса.
г -ФИМ- фазо-импульсная модуляция. Время запаздывания им- пульса t з (фаза) относительного момента квантования зависит от значе- ния исходного сигнала в момент квантования, t з - время задержки импульса.
Наибольшее распространение получили системы с видами моду- ляций АИМ и ШИМ.
Импульсный элемент может входить в любое звено управляющего устройства или объекта. Основные достоинства импульсных САУ опре-деляются прерывистым характером передачи сигналов между отдельными частями системы и состоят в возможности многоточечного управления, в повышенной помехозащищенности и многократном использовании линии связи.
Импульсную САУ мы можем рассматривать как непрерывную САУ, в которой происходит периодическое прерывание контура САУ. Импульсная САУ может быть линейной и нелинейной. Если звенья САУ описываются линейными дифференциальными уравнениями, то она линейна. Общий подход к исследованию импульсных САУ аналогичен рассмотренным ранее.
Цифровыми системами называют дискретные системы, в которых происходит квантование по уровню и по времени. Более точно цифровые системы работают с сигналами в виде цифрового кода. Это наиболее совершенные по своим возможностям САУ. В них роль управляющего устройства играет ЭВМ. На рис.8.11 представлена блок-схема цифровой САУ.
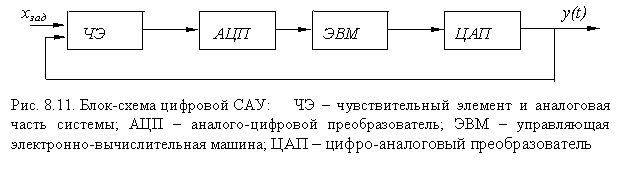
Процесс преобразования непрерывной (аналоговой) величины в цифровой сигнал называют ещё кодированием, а обратный – декодированием.
Цифровые САУ имеют высокую точность, помехозащищенность в них возможна реализация очень сложных алгоритмов управления, многоточечное управление.
В силу широких возможностей и преимуществ цифровые САУ применяют для управления сложными объектами: ракетами, самолетами, кораблями, большими производственными комплексами (энергетическими, химическими и металлургическими комбинатами и т.п.)
8.6. Системы управления с жёсткой программой.
САУ с жесткой программой, блок-схема которой представлена на рис.8.12, не имеет цепи внешней ОС , соединяющей выход с входом .
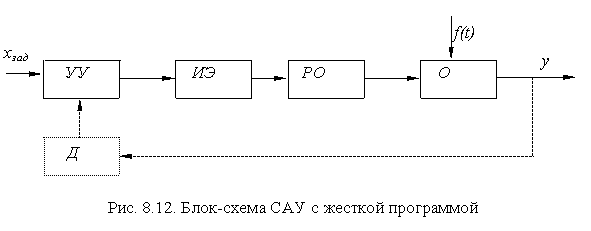
Система работает следующим образом. Сигнал задатчика х зад поступает на управляющее устройство (УУ), преобразующее его в управляющее воздействие, которое после усиления поступает на исполнительный элемент (ИЭ). Последний, перемещая по определенному закону регулирующий орган (РО) вводит на объект (О) управляющее воздействие. В данной САУ выходная (регулируемая) величина не контролируется и не сравнивается с программой. Регулируемая величина может изменяться под влиянием возмущающего воздействия, но система на такие изменения не реагирует. Отсюда следует, что получить высокую точность выходной величины практически невозможно. Если все звенья разомкнутой САУ с жесткой программой устойчивы, то устойчива и вся САУ. Показанная пунктиром связь используется для контроля за выполнением команд, а датчик (Д) дает возможность контролировать положение регулирующего органа.
Слово инвариантный в переводе на русский язык обозначает неизменящийся. В процессе работы любая система испытывает влияние различных вредных возмущающих воздействий. Чтобы реализовать принцип инвариантности к структуре предъявляется требование двухканальности. Принцип двухканальности подразумевает наличие в САУ по меньшей мере двух каналов воздействия возмущения на величину, независимость (инвариантность) которой от этого возмущения должна быть обеспечена.
На рис. 8.13 представлена схема инвариантной САУ, построенная по принципу двухканальности.
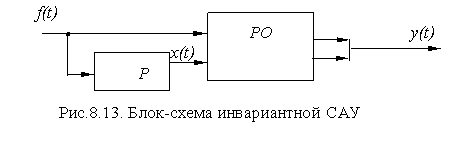
В САУ, построенной по блок-схеме рис. 8.13, объект одновременно испытывает возмущающее воздействие f ( t ) и управляющее воздействие x ( t ), которое сформировано регулятором Р из возмущающего воздействия f ( t ). Причем сформировано таким образом, что оно компенсирует это вредное воздействие f ( t ). Двухканальные системы обеспечивают частичную инвариантность. Плюс ко всему, если эту систему снабдить внешней ОС, то точность работы системы повышается, и мы получаем высокое качество регулирования, которое невозможно получить в обычных замкнутых САУ. В инвариантных системах улучшение качества переходных процессов не влияет устойчивость.
Прежде всего объясним, что такое адаптивные системы. Это системы, которые автоматически изменяют свою структуру и параметры управляющего устройства в зависимости от внешних условий и свойств объекта управления с целью получения необходимого качества управления. На рис. 8.14 показана блок-схема адаптивной САУ.
Данная адаптивная система имеет два контура. Первый контур – основной. Он состоит из основного управляющего устройства (УУО) и объекта управления и представляет собой обычную неадаптивную систему. Второй контур – контур адаптации. Управляющее устройство адаптации УУА изменяет схему УУО и величины его параметров в соответствии с изменениями внешних условий работы и свойств объекта. С этой целью устройство адаптации измеряет f ( t ) и х зад , а также y 1 ( t ) и y 2 ( t ).
К адаптивным САУ относятся самонастраивающиеся САУ со стабилизацией качества управления и самонастраивающиеся САУ с оптими- зацией качества управления.
Первые САУ производят стабилизацию заданного критерия каче- ства путем изменения настройки основного управляющего устройства; вторые, их еще называют экстремальными, поддерживают оптимальными значение критерия качества.
8.9 Самоорганизующиеся и самообучающиеся САУ.
Самоорганизующиеся и самообучающиеся САУ относятся к области кибернетики – науки об управлении.
Самоорганизующиеся САУ (без самообучения) – это разновидность адаптивных САУ, в которых адаптация осуществляется путём изменения алгоритма работы, т.е. происходит изменение структурной схемы основного управляющего устройства. Возможность изменения структуры в ходе адаптации резко расширяет диапазон изменений свойств объекта и внешних условий по сравнению с самонастраивающимися САУ. С течением времени самоорганизация возрастает.
Самообучающиеся САУ своим важнейшим свойством имеют способность к обучению и самообучению, т.е. к самосовершенствованию. Это высший тип систем автоматического управления, обладающих способностью анализа, синтеза информации, отбора и классификации, запоминания, т.е. приближения по своим возможностям к уровню живых разумных существ. Эти САУ требуют принципиально новых подходов к их созданию и исследованию, чем те, что были рассмотрены нами ранее.
<Назад> |