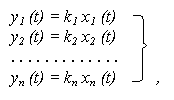Глава 6. СПОСОБЫ ЗАДАНИЯ СТАТИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕМЕНТОВ САУ.

Статические характеристики автоматики могут быть заданы ана- литически или графически.

Если имеем последовательно включенные n -элементов со статическими характеристиками

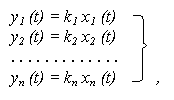( 6.1 )

то, используя свойство последовательного соединения элементов
y i (t) = x i + 1 (t), на основании ( 6.1 ) можно записать упрощенное выражение

y n (t) = k 1 ? k 2 ? ... ? k n x 1 (t) ( 6.2 )

При параллельном соединении n – элементов

x 1 (t) = x 2 (t) = ... = x n (t) = x (t) , ( 6.3 )

а выходная величина будет суммой выходных величин

y (t) = y 1 (t) + y 2 (t) + ... + y n (t). ( 6.4 )

Если же один или несколько элементов охвачен цепью обратной связи, то зависимость выходной величины от входной, имеет вид :

, ( 6.5 )

где x (t) - сигнал на входе; k - коэффициент передачи основной цепи, т.е. при разомкнутой обратной связи; k oc - коэффициент передачи цепи об- ратной связи; y (t) - сигнал на выходе.

Знак “ - “ в формуле ( 6.5 ) соответствует положительной обрат- ной связи, а знак “ + “ соответственно отрицательной.

При наличии нелинейных элементов лучше пользоваться графическими статическими характеристиками. На рис. 6.1г дан пример по- строения результирующей статической характеристики трех элементов, включенных последовательно и имеющих статические характеристики, показанные на рис. 6.1 а,б,в соответственно.

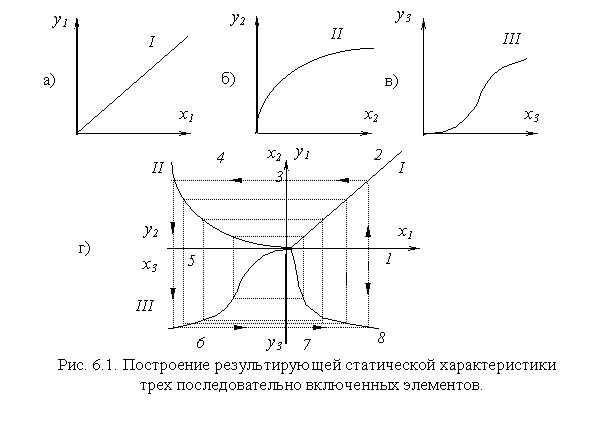
Построение ведется путем представления характеристик элементов в I, II, и III квадрантах рис. 6.1(г). Ось абсцисс характеристики II совмещается с осью ординат характеристики I (т.к. выход первого эле- мента соединен со входом второго); ось абсцисс характеристики III совмещена с осью ординат характеристики II.

Далее на оси х берем точку 1 и идем вверх до пересечения с ха-рактеристикой I и получаем точку 2. Потом поворачиваем параллельно оси х влево и идем до пересечения с характеристикой II и получаем точ- ку 4 ( точка 3 - промежуточная ). После этого идем вниз до пересечения с характеристикой III и получаем точку 6. Теперь на пересечении горизонтали, проведенной через точку 6, и вертикали через точку 1 получаем точку 8. Действуя подобным образом, мы получаем все точки кривой, представляющей результирующую характеристику.

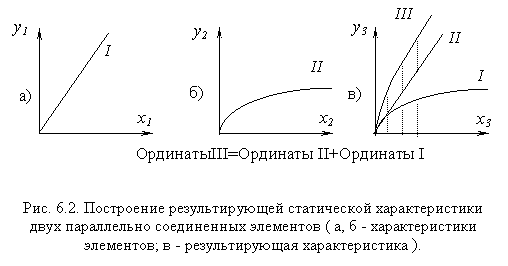
В случае параллельного соединения элементов результирующую характеристику получают путем суммирования ординат отдельных характеристик, представленных в одинаковых масштабах (рис. 6.2).

Рассмотрим теперь построение статической характеристики элемента, охваченного цепью обратной связи. На рис. 6.3 представлены три характеристики: I - статическая характеристика элемента; II – статическая характеристика цепи об-ратной связи; III - результирующая характеристика.

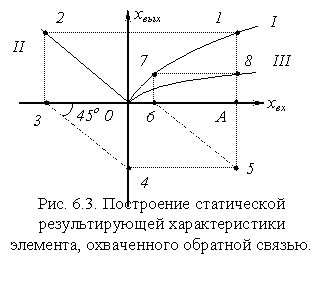
Зададимся некоторой входной величиной х 1 = ОА на оси ОХ и пойдем вертикально вверх до кривой I (точка 1). Теперь пойдем влево по горизонтали до пересечения с кривой II (точка 2) и далее вертикально вниз до пересечения с осью ОХ (точка 3), затем перене- сем этот отрезок на ось ОУ(точка 4). От точки 4 пойдем вправо до пересечения с вертикалью А1 и получим точку 5. Отрезок А5, переносим на ось ОХ от точки А и получаем точку 6. Затем поднимаемся вертикально вверх до кривой I (точка 7) и потом вправо до пересечения с вертикалью А1, получаем точку 8, при-надлежащую кривой III (результирующей кривой). Действуя подобным образом, получим остальные точки.

Таким образом, если нам известны статические характеристики отдельных звеньев (элементов), можно получить статические характери- стики замкнутых систем автоматического управления, дающие зависимость установившегося значения регулируемой величины от установившегося значения одной из входных величин. К входным величинам САУ относится основное возмущающее воздействие (нагрузка на объект) и управляющее воздействие, если есть изменение нагрузки.

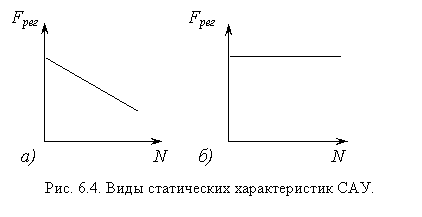
Существуют два вида статических характеристик САУ по нагруз- ке N: характеристика статической системы (рис. 6.4,а) и характеристика астатической системы (рис. 6.4,б ).

6.1. Аналитическое описание объектов регулирования

Работу САУ технологическими процессами можно представить рядом простых операций: движение поступательное или вращательное, заполнение и опорожнение ёмкостей, перемешивание продуктов, изменение освещенности, охлаждение и нагревание и т.д. С точки зрения математического описания такие процессы могут быть представлены одной входной и одной выходной величинами. В качестве примера возьмем электрический водонагреватель (см.рис. 2.2)

Процесс нагрева описывается уравнением:

( 6.6 )

где k - постоянный коэффициент; D Q - результирующее воздействие на объект регулирования ( разность между притоком и расходом энергии или вещества в объекте регулирования ); у - выходная величина.

Как было указано ранее, в нашем случае входные величины - количество подаваемой холодной воды Q , с температурой К х и количество тепла (энергии), отдаваемого нагревательным элементом, пропорционально выделяемой им мощности (или току I ); выходные величины - расход горячей воды Q г с температурой К г . При установившемся режиме все три температуры : нагревательного элемента К н , стенки К с и жидкости К ж , равны между собой (потерями тепла пренебрегаем ).

Допустим, что температура нагревателя К н скачком изменилась на D К н . В этом случае увеличится приток тепла к стенкам и к жидкости. При теплообмене процесс изменения температуры стенки описывается выражением:

( 6.7 )

или

, ( 6.8 )

где V c - объем стенки; g c - плотность стенки; C c - теплоемкость стенки; . a 1 - коэффициент теплоотдачи от нагревательного элемента к . стенке бака; S c - площадь поверхности стенки бака.

Разделив теперь ( 6.8 ) на a 1 S c и заменив на Т 1 , получим

( 6.9 )

и перейдем к операторной форме

( Т 1 р + 1 ) D К с ( р) = D К н ( р) ( 6.10 )

Изменение температуры жидкости с повышением температуры стенки описывается уравнением:

( 6.11 )

или

( 6.12 )

где V ж - объем жидкости; g ж - плотность жидкости; С ж - теплоемкость жидкости; a 2 - коэффициент теплоотдачи от стенки к нагреваемой жидкости; S ж - площадь внутренней поверхности стенки бака. Разделим также ( 6.12 ) на a 2 S ж и, обозначив , получим

( 6.13 )

или в операторной форме

( Т 2 р + 1 ) D К ж (р) = D К с (р) ( 6.14 )

Подставим в уравнение (6.9) значение для D К с из уравнения (6.13) получим в операторной форме:

( 6.15 )

и далее, подставив (6.15) в (6.14), получаем

( 6.16 ) или

( Т 1 р + 1 ) ( Т 2 р + 1 ) D К ж ( р) = D К н ( р) ( 6.17 )

Запишем теперь уравнение объекта регулирования в окончательном виде:

[ Т 1 Т 2 р 2 + ( Т 1 + Т 2 ) р + 1 ] D К ж ( р) = D К н ( р), ( 6.18 )

которому соответствует дифференциальное уравнение

( 6.19 )

6.2. Определение статических и динамических характеристик регулируемых объектов

Рассмотренные ранее аналитические выражения для статических и динамических характеристик объектов получены для сравнительно простых объектов. Для сложных объектов получение аналитических выражений дело очень трудоемкое и обычно их определяют экспериментально. В этом случае можно воспользоваться схемой эксперимента, по- казанной на рис. 6.5.

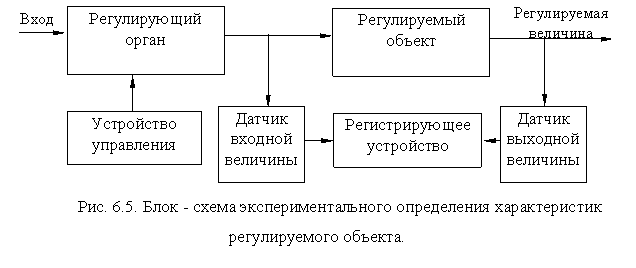
Статическую характеристику определяют так. Вручную (либо дистанционно) установленный в линии притока энергии или продукта регулирующий орган переводят из одного положения в другое, добиваясь каждый раз равновесного состояния. Измеряя входные и соответствующие им выходные величины, строят график зависимости у = f(х), что и будет статической характеристикой. Для лучшего проведения опыта его повторяют несколько раз, изменяя входную величину от x min до x max и получая соответственно y min и y max , а потом наоборот от х max до x min .

Снятие динамических характеристик является более трудоемким процессом. Прежде всего, следует оценить экспериментально длительность переходного процесса. Далее поступают следующим образом:

1)добиваются установившегося состояния объекта путем стабилизации входной величины;

2) делают выдержку в течение 20...30 с при быстро изменяющихся величинах и 120...150 с при медленно изменяющихся величинах;

3) с помощью регулирующего органа скачком изменяют входную величину и фиксируют изменение выходной величины во времени.

Величина скачка выходного воздействия должна составлять 5...15% от максимального значения входной величины. Это лимитируется тем, что в любом объекте могут быть нелинейности, а при очень малых воздействиях начинают сильно влиять помехи. Следует также следить, чтобы режим работы объекта не изменялся и чтобы другие воздействия оставались постоянными. Необходимо также отметить, что на точность результатов будут влиять временные характеристики измерительных приборов (устройств). Это следует учитывать при их выборе. Переходный процесс считается законченным при достижении в объекте установившегося значения скорости изменения регулируемой величины (астатический объект) или нового установившегося значения регулируемой величины (статический объект).

На рис.6.6 показаны наиболее характерные кривые, представляющие собой динамические характеристики объектов. По полученным характеристикам можно построить математические модели данных объектов и далее их использовать для исследования САУ.

Эти характеристики (рис. 6.6) не могут быть непосредственно использованы при расчете систем автоматического регулирования. Они должны быть в конечном итоге представлены аналитически, чтобы можно было написать дифференциальные уравнения звена или всего объекта.

<В начало>

<Содержание>