Ранее мы рассмотрели уравнения, описывающие то или иное звено САУ. Зная уравнения отдельных звеньев, возможно составить уравнение всей системы САУ. Но наиболее простым и легким является путь получения этих уравнений по структурным схемам САУ. Еще проще проводить анализ и синтез САУ, используя передаточные функции, так как они однозначно связаны с дифференциальными уравнениями. Поскольку нас интересует замкнутая САУ, то дадим ее определение. Замкнутой САУ называется система, имеющая главную обратную связь - обратную связь между входом и выходом.
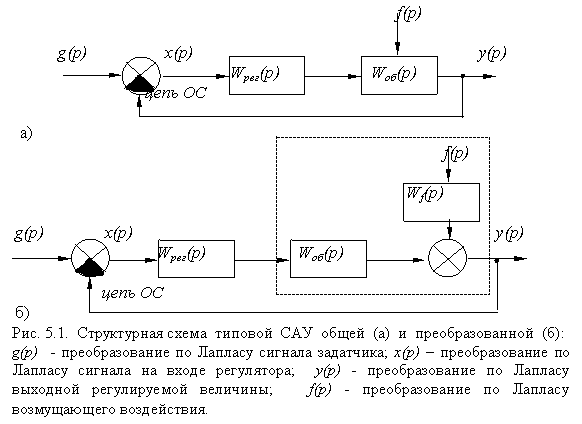
Блок - схему САУ представим в несколько преобразованном виде - структурной схемой ( рис. 5.1 ) и для дальнейшего рассмотрения приведем некоторые оределения и параметры, а также соотношения между ними.
5.1. Передаточная функция разомкнутой и замкнутой системы
Передаточная функция разомкнутой системы N(p) определяется как отношение у(р) к х(р) при нулевых начальных условиях. Это понятие имеет смысл, если разорвать цепь главной обратной связи. На рис. 5.1. представлена структурная схема САУ с разбиением на две части: регулятор (в него входит чувствительный элемент) и объект. Соответственно обозначим через W рег (р) - передаточную функцию регулятора , через W об (р) - передаточную функцию объекта и через W f (p) - передаточную функцию объекта по возмущающему воздействию f(p). Преобразова- ние схемы рис. 5.1 (а) в схему рис. 5.1 (б) произведено по правилу переноса воздействий.

Для разомкнутой САУ можно записать:
![]() ( 5.1 )
( 5.1 )
или в более общем виде
![]() ( 5.2 )
( 5.2 )
где В(р) = N рег (р) ? N об (р) ; С(р) = Q рег (р) ? Q об (р);
B(p) = b 0 p m + ... + b m ; C(p) = c 0 p n + ... + c n .
Причем вещественные коэффициенты С и С i зависят от параметров звеньев САУ. Для реальных САУ b m ? 0 и m < n . Многочлен С(р) называют характеристическим полиномом разомкнутой системы, а уравнение
С(р) = 0 ( 5.3 )
представляет собой характеристическое уравнение разомкнутой САУ. . Если один или несколько младших коэффициентов многочлена С(р) равны нулю ( c n = c n-1 = ... = c n - ![]() +1 = 0, a
+1 = 0, a ![]() = 0, 1, 2 ...), то выраже- ние для передаточной функции разомкнутой системы мы можем записать так:
= 0, 1, 2 ...), то выраже- ние для передаточной функции разомкнутой системы мы можем записать так:
![]() ( 5.4 )
( 5.4 )
Как правило, передаточную функцию разомкнутой системы представляют в стандартном виде - многочлены числителя и знаменателя имеют свободные члены, равные 1. Применительно к нашей передаточной функции это будет так:
![]() ( 5.5 )
( 5.5 )
где
![]() ( 5.6 )
( 5.6 )
a B i = b i / b m , i = 0, 1, ...m ; C i = c i / c n - v , i = 0, 1, ... n – v.
Величина ![]() называется порядком астатизма САУ относительно g(t), а параметр
называется порядком астатизма САУ относительно g(t), а параметр
![]() ( 5.7 )
( 5.7 )
называется коэффициентом усиления разомкнутой системы ( размерность его с -1 ). Физически -это есть отношение ![]() - ой производной выходной (ре-гулируемой ) величины к постоянной ошибке x 0 .
- ой производной выходной (ре-гулируемой ) величины к постоянной ошибке x 0 .
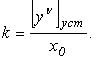 ( 5.8 )
( 5.8 )
Если ![]() = 0 , то имеем статическую САУ и ее передаточная функ- ция :
= 0 , то имеем статическую САУ и ее передаточная функ- ция :
![]() ( 5.9 )
( 5.9 )
Если же ![]() = 1, то мы будем иметь САУ с астатизмом 1 го поряд- ка, и ее передаточная функция :
= 1, то мы будем иметь САУ с астатизмом 1 го поряд- ка, и ее передаточная функция :
![]() ( 5.10 )
( 5.10 )
При расчете процессов в замкнутых САУ используют помимо передаточной функции разомкнутой системы еще три основные передаточные функции: главную передаточную функцию (главный оператор), передаточную функцию замкнутой системы для ошибки (сигнала рассогласования), передаточную функцию замкнутой системы по возмущающему воздействию.
Главная передаточная функция замкнутой системы Ф(р) определяется при отсутствии возмущающих воздействий ( т.е. f(t) = 0 ) как отношение у(р) к х(р) при нулевых начальных условиях. Приведем
структурную схему рис. 5.1 (а) к виду рис. 5.2.
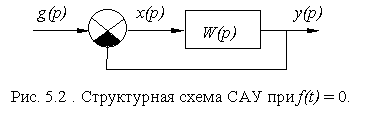
Для этой структурной схемы имеем:
x (p) = g (p) - y (p); y (p) = x (p) ? W (p) ( 5.11 )
Тогда
![]() ( 5.12 )
( 5.12 )
Из формулы ( 5.11 ) находим
у (p) = W (p) [ g (p) - y (p) ], ( 5.13 )
откуда с учетом ( 2.18 ) получаем
![]() ( 5.14 )
( 5.14 )
где N (p) и Q (p) многочлены числителя и знаменателя передаточной функции разомкнутой системы W (p), a D (p) - характеристический полином замкнутой системы.
D (p) = Q (p) + N (p) ( 5.15 )
5.2. Передаточная функция замкнутой системы для ошибки ( сигнала рассогласования )
Передаточную функцию замкнутой системы для ошибки Ф х (р) определяем, положив возмущающее воздействие равным нулю, т.е. по структурной схеме рис. 5.2.
![]() ( 5.16 )
( 5.16 )
учитывая формулу ( 5.11 ), получаем
![]() . ( 5.17 )
. ( 5.17 )
5.3. Передаточная функция замкнутой системы по возмущающему воздействию
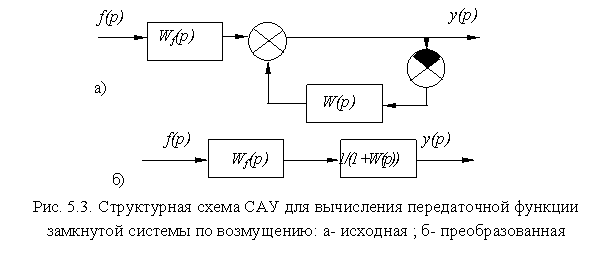
Положив g (t) = 0 , преобразуем структурную схему рис. 5.2 в схему рис. 5.3.
Тогда
![]() ( 5.18 )
( 5.18 )
При g (p) = 0 из схемы рис. 5.3 имеем
y (p) = W (p) [ - y (p) ] + W f (p) ? f (p) , ( 5.19 )
откуда
![]() ( 5.20 )
( 5.20 )
где R (p) = Q (p) ? W f (p) , причем R (p) зависит от места приложения возмущающего воздействия в системе. Кроме того, нужно обратить внимание на тот факт , что при g (t) = 0 мы имеем х (р) = - у (р) и передаточная функция системы ошибки по возмущающему воздействию Ф х (р) = х (р) / f (p) будет иметь то же выражение, что и для регулируемой величины.
Для всей замкнутой системы рис. 5.5 имеем
![]() (5.21)
(5.21)
или