Рассмотрим уравнения, переходные характеристики и частотные характеристики наиболее часто встречающихся звеньев в системах автоматического управления сельхозмашинами.
Данное звено, как в статике, так и в динамике описывается уравнением (2.1)
y = kx .
Примерами такого звена в механике могут быть редуктор без люфта, в электронике - усилитель без реактивных элементов (на сопротивлениях). К такому типу звена относятся очень многие датчики сигналов.
Передаточная функция такого звена равна постоянной величине
W( p ) = k . ( 3.1 )
Очевидно, что при формальной замене р = jw, т.е. переходе в частотную область, получаем частотную передаточную функцию этого звена
W( jw ) = k
При этом амплитудная частотная характеристика также равна постоянной величине:
A( w ) = | W(jw) | = k,
а фазовая частотная характеристика равна нулю:
j( w ) = arg [ W(j w) ] = 0
Амплитудно-фазовая характеристика в этом случае вырождается в точку на вещественной оси. На рис. 3.1 представлены характеристики этого звена, где а- передаточная функция, переходная характеристика, .
функция веса; б- частотная передаточная функция, АФХ, АХ и ФХ, ЛАЧХ и ЛФЧХ.
3.2. Апериодическое звено первого порядка
Данное звено описывается следующим дифференциальным уравнением
( 3.2 )
Передаточная функция звена
. ( 3.3 )
В качестве примеров можно привести следующие: двигатели электрические и гидравлические, электрический генератор, нагревательная печь и т.п. На рис. 3.2 приведены характеристики этого звена: а- передаточная функция, переходная характеристика, функция веса; б- частотная передаточная функция, ЛФХ, АХ и ФХ, ЛАЧХ, ЛФЧХ.
Из графика переходной характеристики и функции веса нетрудно определить параметры k и Т. Для определения Т проводим касательную к кривым в точке t = 0 и на пересечении ее с осью t находим величину постоянной времени Т. Время переходного процесса принимаем равным 3Т. Из графика АЧХ видно, что звено пропускает сигналы с частотой w < 1/Т с коэффициентом передачи близким к k. За полосу пропускания звена принимают величину
Для ЛАЧХ этого звена имеем
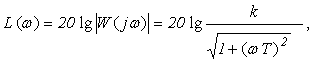(3.4)но по точкам строить эту функцию нет никакой необходимости. Обычно строят так называемую асимптотическую ЛАЧХ, состоящую из отрезков прямой ( см. рис. 3.3).
Через точку w = 20 с-1 проведена вертикальная прямая w = 1/Т (w - так называемая сопрягающая частота). Левее этой точки w< 1/Т и
L( w ) » 20 lg k.
На рис. 3.3 этому выражению соответствует отрезок ab , параллельный оси w. Это первая асимптота.
Справа от вертикали w = 1/Т ( при w>1/Т) имеем
Для этого случая получим отрезок bc c наклоном - 20дБ/дек, и это будет вторая асимптота.
Аналитически построенная ЛАЧХ будет отличаться от асимптотической только в окрестности точки b и наибольшее отклонение будет иметь место при w = 1/Т
Если k= 1, то 
дБ 
3 дБ.
Это весьма незначительная ошибка, которая не имеет существенного значения. ЛФЧХ j(w) = - arc tg wT строится по точкам. Эта зависимость симметрична относительно точки j ( 1/Т) = - 450 и не зависит от k. На практике пользуются нормированной ЛФЧХ, определяемой выражением
где w0 = 1/Т ( рис. 3.4 )
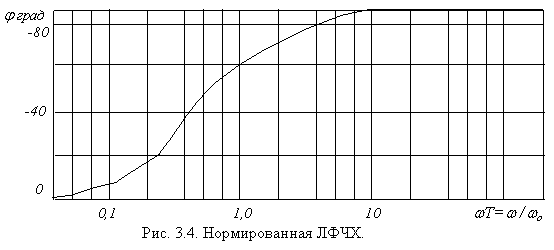
Наложим теперь рис.3.4 на рис.3.3 так, чтобы совпали оси час- тот (масштаб должен быть одинаков), и начнем перемещать кривую j(w /w0) до совпадения вертикали w /w0 = 1 с частотой w = 1/Т ЛАЧХ. Теперь, просто обведя контур нормированной ЛФЧХ, получим обычную ЛФЧХ.
3.3. Апериодическое звено второго порядка
Пусть динамическое звено описывается дифференциальным уравнением второго порядка:
( 3.5)
Если а21 > 4а2a0 , то имеет место достаточно большое трение (сопротивление) и корни характеристического уравнения а0 р2 + а1р + а2=0 будут вещественными, т.е. процесс будет апериодическим, а звено – относится к апериодическим звеньям второго порядка и его передаточная функция будет иметь вид
( 3.6 )
где Т1 = а1 / а2 ( с ) ; Т22 = а0 / а2 ( с2 ) - постоянные времени.
Примером апериодического звена второго порядка может служить электродвигатель постоянного тока с независимым возбуждением.
Колебательное звено описывается также дифференциальным уравнением второго порядка (3.5) , а его передаточная функция определяется выражением (3.6) с той лишь разницей, что затухание в этой сис- теме гораздо меньше. Иными словами корни характеристического урав- нения (а0 р2)/a2 +( а1 р)/a2 +1=0 являются комплексными, т.е. а21 < 4а2 a0.
Уравнение (3.5) записывают в виде:
( 3.7 )
где 2x Т1 = Т2 = Т
или в операторной форме:
( Т2 р2 + 2x Тр + 1) у( р) = kx( p), ( 3.8 )
причем wрез = 1/ Т - резонансная частота звена; x - параметр затухания, 0< x <1, при x ³ 1 будем иметь апериодическое звено второго порядка.
На рис. 3.5 представлены характеристики колебательного звена
Полученная из уравнения (3.8) АЧХ этого звена
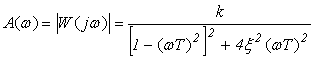( 3.9 )
при x < 1/ 
имеет резонанс.
При этом резонансная частота
( 3.10 )а высота пика . . . ( 3.11 )
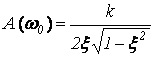
Если E–›0, то A(w)–›
, а выражение для ЛАХ имеет вид
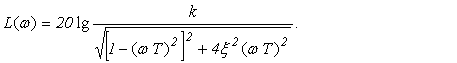(3.12)
Асимптотическая ЛАХ рис. 3.6 ( кривая 1) определяется уравнениями:
L (w) » 20 lg k при w< 1/Т; L (w) » 20 lg k / (wT)2 при w> 1/ Т.
Кривая 2 построена по точкам, полученным из выражения (3.9). Здесь следует за- метить, что возможно использовать универсальные кривые поправок к ЛАХ. При наличии ЭВМ этот вопрос не представляет никакой трудности. Мы не рассматриваем формулы для расчета ФЧХ, т.к. это легко сделать по формулам (2.29).
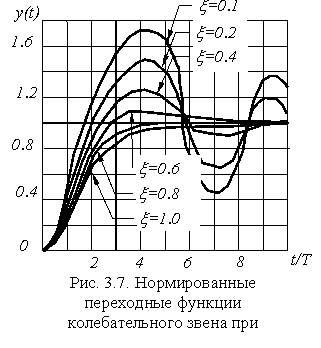
На рис. 3.7 приведено семейство нормированных переходных функций колебательного звена при k=1. На них хорошо просматривается влияние величины x на вид переходного процесса.
В качестве аргумента переходных функций взято относительное время t /Т, т.е. кривые пригодны для любых значений постоянной Т. Если k¹1, то их ординаты нужно умножить на величину k. Из анализа кривых видно, что чем меньше x, тем переходный процесс носит более выраженный колебательный характер.
3.5. Идеальное интегрирующее звено
Уравнение интегрирующего звена имеет следующий вид:
( 3.13 )
а передаточная функция:
( 3.14 )
На рис. 3.8 показаны временные, а на рис. 3.9-частотные характеристики интегрирующих звеньев.
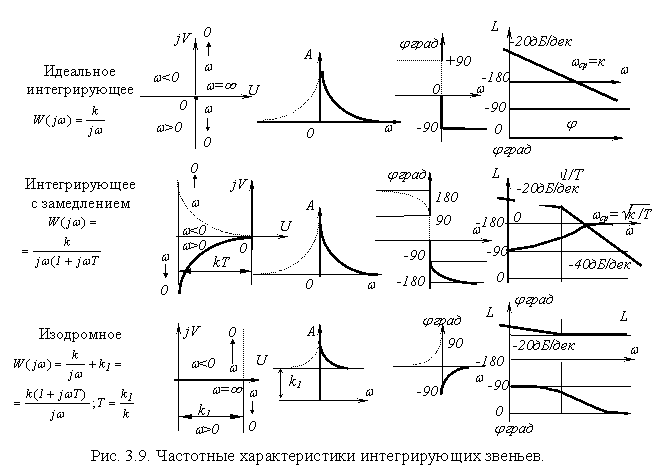
АФХ идеального интегрирующего звена сливается с мнимой осью. Отрицательная часть оси относится к положительным частотам. Из ее рассмотрения напрашивается вывод, что чем ниже частота подаваемого сигнала, тем лучше он пропускается интегрирующим звеном.
3.6. Интегрирующее звено с замедлением
Его уравнением является:
( 3.15 )
передаточная функция:
( 3.16 )
Обратим внимание на формулу (3.16). Следует отметить, что на практике мы имеем дело с такими интегрирующими звеньями. Наиболее типичным примером интегрирующего звена с запаздыванием является двигатель, если выходной величиной считается угол поворота выходного вала.
Судя по формуле (3.16) , W( p ) есть произведение
что эквивалентно последовательному соединению интегрирующего и апериодического первого порядка звена. Это будет показано в следующем параграфе. Характеристики этого звена также показаны на рис. 3.7 и рис. 3.8.
Уравнение изодромного звена несколько необычно:
( 3.17 )
а его передаточная функция:
( 3.18 )
где Т = k1 / k.
Из выражения (2.15) видно, что звено эквивалентно параллель- ному соединению двух звеньев ( см. параграф 2.4 ) с передаточными функциями k / p (идеальное интегрирующее ) и k1 ( безынерционное). Примером в технике может служить центробежный регулятор скорости.
Временные характеристики звена и его частотные характеристики даны на рис. 3.8 и на рис. 3.9.
Асимптотическая ЛАХ изодромного звена имеет вид:
( 3.19 )
строится следующим образом. На оси частот отмечается точка w = k и через нее проводится первая асимптота ЛАХ с наклоном - 20дБ / дек до пересечения с вертикалью w = 1/Т. Из точки пересечения первой асимпто- ты и вертикали проводится вторая асимптота - горизонталь. На частотах, меньше сопрягающей частоты w = 1/Т, звено представляет собой идеаль ное интегрирующее звено, а на частотах w >> 1 / Т - безынерционное с коэффициентом передачи k1 = kT.
3.8. Идеальное дифференцирующее звено
Для этого звена имеем уравнение:
( 3.20 )
и передаточную функцию:
W( p ) = kp . ( 3.21 )
Характеристики этого звена представлены на рис.3.10 и на рис.3.11. В технике такому звену может соответствовать дифференцирующий усилитель.
3.9. Дифференцирующее звено с замедлением
Это звено описывается уравнением:
( 3.22 )
и имеет передаточную функцию:
( 3.23 )
Из передаточной функции видно, что звено эквивалентно последовательному соединению двух звеньев с передаточными функциями kp (идеальное дифференцирующее звено ) и 1/(1+Тр) ( апериодическое звено первого порядка). В технике примерами могут быть электрические дифференцирующие цепи.
Характеристики этого звена также приведены на рис. 3.10 и на рис.3.11.
3.10. Звено с постоянным запаздыванием.
Данное звено передает входной сигнал на выход без искажения, но с запаздыванием на время t.
Уравнение такого звена имеет вид:
y(t) = x ( t - t ) , причем. при t < t y = 0 ( 3.24 )
Характеристики этого звена имеют вид:
А( w ) =1 ( 3.25 )
( w ) = - tw
Амплитудно - фазовая частотная функция
W( jw ) = e-jwt ( 3.26 )
передаточная функция.
W( p) = e -t p ( 3.27 )
Рис.3.11 Частотные характеристики дифференцирующих звеньев.
Проанализируем выражение (2. 13 )
Q( p ) y( p ) = N( p ) x( p )
для звена первого и второго порядков.
Для звена первого порядка мы имеем
(Тр + 1 ) у( р ) = k x( p )
В этом случае
Q( p ) = Tp + 1 , a N( p) = k
Для звена второго порядка
(T22 p + T1 p + 1 ) y(p ) = k( p ) x( p ),
здесь Q( p) = T22 p - T1 p + 1 ; N(p) = k(p) = k - как в рассмотренном ранее случае.
Многочлен Q (p) называется собственным оператором элемента, а N(p) - оператором воздействия на элемент или операторным коэффициентом усиления.
Наиболее часто встречаются следующие собственные операторы элементов:
Тр + 1 - одноёмкостный элемент или апериодический первого порядка;
Т22 р + Т1 р + 1 - колебательный элемент;
Т2р2 + 1 - консервативный (накапливающий) элемент (колебательный контур без затухания);
Тр - астатический элемент или интегрирующее звено;
Тр-1 - неустойчивый элемент;
Операторы воздействий N (p) чаще всего встречаются следующих видов: k ; k + ap ; k + ap + bp2. Параметры a и b иногда бывают отрицательными.
Если N(p) = k = const, то воздействие называется статическим; если N(p) = k + ap, то кроме статического воздействия есть воздействие по первой производной, а при N(p) = k +ap + bp2 , то еще по второй производной. Эти операторы еще называют и типовыми звеньями.
<Назад> |