Чтобы грамотно составлять чертежи поверхностей вращения и решать с ними задачи надо четко представлять операцию вращения точки и уметь передать эту операцию чертежом.
Пусть некоторая точка А вращается вокруг вертикальной оси j. Вращение точки происходит по окружности, радиус которой RА. Окружность - плоская кривая. Плоскость окружности вращения ZА - горизонтальная, поэтому горизонтальная проекция окружности не искажена, а фронтальная - отрезок прямой, величина которого равна 2RА. Центр окружности вращения точки А - точка 0 . Это точки пересечения оси j и ZА .
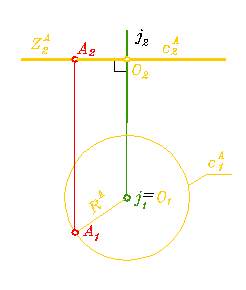
Рис. 184 На рисунке 184 представлена операция вращения точки А вокруг оси j. У любой поверхности вращения при движении каждая точка вращается
по своей окружности, которую называют параллель
. Самая большая среди ближайших параллель называется экватором , самая маленькая - горлом (рис. 185). У поверхности может быть несколько горл
и экваторов. У некоторых поверхностей вращения горло может выродиться в точку.
Например, у сферы, конуса, эллипсоида вращения. Экватор может совпадать с линией
активного обреза. Например, у конуса, однополостного гиперболоида вращения,
параболоида вращения и т.д.
(Открыть в своём
проигрывателе) Плоскость, которая проходит через ось вращения, рассекает поверхность
вращения по меридиану . Если эта плоскость параллельна
плоскости проекций, то меридиан проецируется без искажения. Такой меридиан
называется главным. Среди множества поверхностей вращения в технике нашли широкое
применение те, у которых образующая - прямая, то есть линейчатые поверхности
вращения: конус, цилиндр. однополостный гиперболоид вращения (см рис
189, 191, 193, 193-а), а также
те, у которых меридиан окружность или ее часть, кривая второго порядка. Название
последних определяется названием кривой: параболоид вращения
(рис. 187), эллипсоид вращения (рис. 186-a,
186-б), гиперболоид вращения двуполостный
(рис. 188). У двуполостного гиперболоида вращения ось вращения совпадает
с действительной осью гиперболы, а у однополостного (рис 193-a)-
с мнимой.
(Открыть в своём
проигрывателе)
(Открыть в своём
проигрывателе) Вид. 14
Вид.15
(Открыть в своём
проигрывателе) Вид. 16 Геометрическая часть определителя линейчатых поверхностей содержит
прямолинейную образующую и ось вращения, алгоритмическая - закон движения (вращения)
образующей и информацию об относительном положении образующей и оси. В зависимости
от последнего условия могут сформироваться три линейчатые поверхности вращения. Q
((li , j, S) : li Q
((li , j) : li
Невозможно перечислить все примеры применения поверхностей конусов и цилиндров
вращения, так как это самые технологические после плоскости поверхности. Из
всех поверхностей вращения только они являются развертывающимися. X
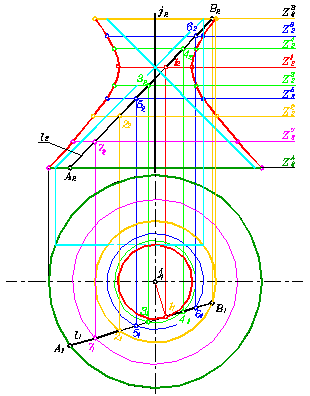
((li , j) : li На рис. 194 представлено построение основного чертежа
однополостного гиперболоида вращения, ось которого горизонтально-проецирующая
прямая, образующая - отрезок общего положения. Аудио-комментарии Рис. 194-а Аудио-комментарии Рис. 194-б Аудио-комментарии Проведём построения. Определим радиус горла. Ближайшая к оси точка на образующей
определяется на горизонтальной проекции, на которую ось спроецировалась в точку
- j1. Очевидно, горизонтальные
проекции центров всех параллелей совпадут с j1.
Поэтому из j1 проводим
прямую, перпендикулярную к проекции образующей А1В1
до пересечения в точке 11.
Окружность радиусом j1 - 11
является горизонтальной проекцией горла. С помощью вертикальной линии связи
на А2В2
находим 12. На высоте точки
12 располагается горло.
Проводим горизонтальную линию через 12
и на ней от оси откладываем по обе стороны отрезок, равный радиусу горла ( на
чертеже горло изображено красным цветом). Для построения верхнего граничного экватора, содержащего точку
В, проводим окружность радиусом j1
- В1 (оранжевым цветом)- что
является горизонтальной проекцией экватора с точкой В,
и на высоте В2 от проекции оси
j2 откладываем по обе стороны
отрезки, равные радиусу экватора с точкой В. Анализируя горизонтальную проекцию., устанавливаем:
оранжевая параллель пересекает АВ ещё и в точке
21. Безусловно, по другую
сторону по вертикали от горла должна симметрично относительно него располагаться
ещё одна параллель. Её высоту можно определить двояко - пользуясь симметрией
относительно плоскости горла или с помощью проекции 22
на А2В2.
Для определения проекций нижнего граничного экватора, содержащего точку А,
проводим аналогичные построения тёмно-зелёным цветом. Построение промежуточных параллелей рассмотрим на примере зелёной,
содержащей точки 3 и 4. Радиус этой параллели несколько больше радиуса горла. Горизонтальная
проекция зелёной параллели пересекает горизонтальную проекцию образующей А1В1
в точках 31 и 41.
С помощью вертикальных линий связи определяем проекции 32
и 42 на А2В2. Как
видим, по высоте они симметричны относительно плоскости горла. Теперь на уровне
проекций 32 и
42 строим вырожденные проекции зелёных
параллелей. Выполняя подобные построения синим и сиреневым цветом получим фронтальные
проекции очерковых точек на уровне параллелей точек 52
, 62 и 72
. Соединяем проекции очерковых точек плавными кривыми, получаем проекции ветвей
гиперболы. Посмотрите внимательно на голубые образующие, проведённые касательно
к горлу на горизонтальной проекции. Их фронтальные проекции являются асимптотами
построенных гипербол. А то, что они симметричны объясняется свойством однополостных
гиперболоидов: эти поверхности дважды линейчатые. На рис. 194-б представлен основной
чертёж построенного гиперболоида вращения. Если считать, что его оболочка снаружи
жёлтая, а внутри зелёная, то очевиден просвет горла на горизонтальной проекции. На рис. 195 приведены построения
недостающих проекций точек, принадлежащих построенной нами поверхности однополостного
гиперболоида вращения, заданного графическим определителем. Рис. 195 Аудио-комментарии Однополостные гиперболоиды вращения
применяются в строительстве радиомачт, градирен, водонапорных башен, в зубчатых
и фрикционных передачах в механизмах, оси которых скрещиваются. Так первая
радиомачта в Москве в Шаболовке была построена инженером Шуховым в 1926 году
из отсеков, подобных построенному нами с убывающими вверх радиусами оснований. Если вокруг прямой оси вращать окружность, расположенную с
ней в одной плоскости, то сформируется торовая поверхность или как частный случай
- сфера . Торы бывают: открытый тор или кольцо (рис. 196
- 199); (Открыть в своём
проигрывателе)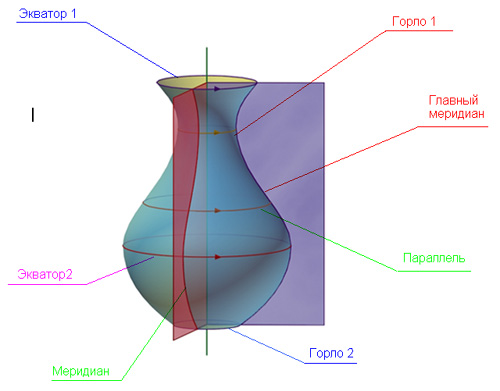
Рис. 185
Вид. 13
Рис. 187
Рис. 186-а
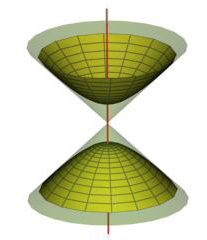
Рис. 188-а
Линейчатые поверхности вращения
![]() j = S ; (li ^ j) = const)
j = S ; (li ^ j) = const)![]() j ; li || j ; [ li , j ] = const)
j ; li || j ; [ li , j ] = const)
Рис. 191
![]() j ; li И j ; [ li, j ] = const)
j ; li И j ; [ li, j ] = const)
Торовые поверхности вращения
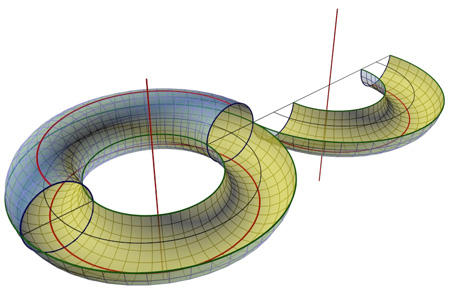 Открытый тор
Открытый тор
Вид. 25
На рис. 196 представлен графический определитель открытого тора - кольца. На рис. 197 выполнено построение недостающих проекций точек , лежащих на поверхности кольца, заданного графическим определителем.
|
Рис. 196 |
Рис. 197 |
У открытого кольца экватор и горло находятся на одном уровне с круговой осью - траектории перемещения центра образующей окружности. Экватор - самая большая внешняя параллель тора , горло - самая маленькая внутренняя.
|
Рис. 198 |
Рис. 199 |
На рис. 198 представлены точки, лежащие на особых параллелях кольца: зеленым цветом показаны горло и экватор, красным - опорные паралели, по которым кольцо можно совместить с плоскостью
На рис. 199 выполнено построение недостающих проекций точек, принадлежащих поверхности открытого тора на основном чертеже.
В качестве носителей точек на поверхностях вращения выбирают параллели, которые на одну из плоскостей проекций проецируются без искажения. Принадлежность точки торовой поверхности можно установить как по основному чертежу (рис. 198, 199, 202, 205, 207 - 209), так и по графическому определителю (рис. 197). Важно помнить, что у поверхностей вращения радиус параллели всегда равен расстоянию от оси до главного меридиана и обязательно учитывать видимость заданной проекции точки!
Закрытый тор (рис. 200 )
|
|
Закрытый тор |
В данном случае горло - выродилось в точку касания образующей окружности и оси.
Самопересекающийся тор (рис. 201)
У такого тора два горла - точки пересечения образующей окружности с осью
|
|
Самопересекающийся тор |
У всех торовых поверхностей четвертого порядка есть еще одна примечательная параллель, которую можно назвать опорной , потому что именно на ней будет лежать торовая поверхность на горизонтальной плоскости. Опорная параллель является границей внутренних и внешних параллелей. Опорных параллелей две. Они расположены симметрично относительно плоскости экватора. Радиус опорной параллели равен радиусу круговой оси тора.
Сфера (рис. 207)
|
|
Сфера |
Торовая поверхность второго порядка (рис. 208).
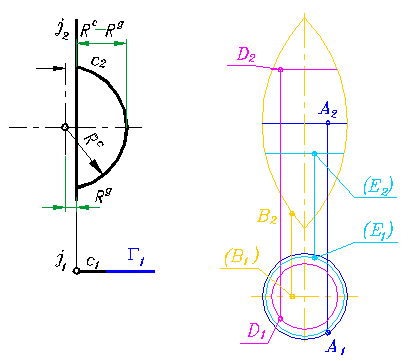
Рис. 208
Торовая поверхность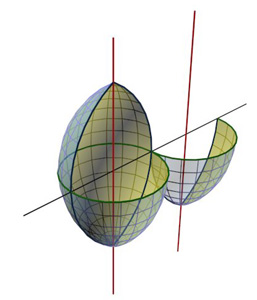 второго
порядка
второго
порядка
Все торовые поверхности замкнутые.
В технике применяется еще одна торовая поверхность - глобоид (рис. 209), но ее следует рассматривать как внутренний отсек кольца.
|
|
Глобоид |
(Открыть в своём
проигрывателе)
Вид. 26
Для закрепления изучаемого материала решите задачи: №46(1), №46(2), №46(3), №46(5)
Вопросы для самопроверки:
1. Что такое параллель у поверхности вращения?
2. Что называется меридианом?
3. Какой меридиан называется главным?
4. Где у глобуса горло?
5. Сколько можно создать линейчатых поверхностей вращения? Назовите их.
6. Что построил инженер Шухов из поверхностей вращения?
7. Повторите построение рисунков 194а и 195?
8. Как образовать торовую поверхность?
9. Какие бывают торы?
10. Какой тор является квадратным?
11. Как узнать порядок тора?
12. Частью какой поверхности является глобоид?
13. Что такое гелиса?
14. Какие бывают геликоиды?
15. У какого геликоида есть конус параллелизма?