Раздел 1:
Раздел 2:
Раздел 3:
Раздел 4:
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Что такое метрология?
Метрология – это наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности. Измерения физических величин, технических параметров, характеристик процессов, состава и свойств веществ, размеров основаны на практическом использовании положений метрологии. Термины и определения в метрологии устанавливает РМГ 29-99.
Метрологию подразделяют на общую (теоретическую и экспериментальную), прикладную и законодательную.
Теоретическая метрология: раздел метрологии, предметом которого является разработка фундаментальных основ метрологии. Иногда применяют термин "фундаментальная метрология". Общая метрология занимается фундаментальными исследованиями, разработкой общей теории измерений, формированием систем единиц измерений, созданием эталонов, стандартных образцов состава и свойств веществ и материалов, мер и определением физических постоянных.
Практическая (прикладная) метрология: раздел метрологии, предметом которого являются вопросы практического применения разработок теоретической метрологии и положений законодательной метрологии. Прикладная метрология занимается решением практических задач, важнейшими из которых являются создание методов и рабочих средств измерений с целью обеспечения единства измерений
Законодательная метрология - раздел метрологии, предметом которого является установление обязательных технических и юридических требований по применению единиц физических величин, эталонов, методов и средств измерений, направленных на обеспечение единства и необходимой точности измерений в интересах общества.
Законодательная метрология служит средством государственного регулирования метрологической деятельности посредством законов и законодательных положений, которые вводятся в практику через Государственную метрологическую службу и метрологические службы государственных органов управления и юридических лиц. К области законодательной метрологии относятся испытания и утверждение типа средств измерений, их поверка и калибровка, сертификация средств измерений, государственный метрологический контроль и надзор за средствами измерений.
Что такое измеряемые свойства и их меры?
Измерительная задача заключается в получении конкретных количественных данных о материальном объекте, который в свою очередь характеризуется наличием определенных свойств. Любое свойство может проявляться в большей или меньшей степени, т.е. имеет количественную характеристику. Следовательно, любое свойство может быть измерено.
Каждое свойство может быть охарактеризовано по-разному. Свойство нагретости тел, например, может характеризоваться средней скоростью теплового движения молекул, а может термодинамической температурой. Свойство пространственной протяженности можно характеризовать расстоянием между двумя точками пространства, а можно - углом между направлениями на них из точки наблюдения. Неопределенность числового значения случайной величины характеризуется энтропией или доверительным интервалом при выбранной доверительной вероятности и т.д. Понятно, что для удобства общения и обеспечения единства измерений все должны пользоваться одинаковыми характеристиками. Их называют мерами. Согласованные меры узакониваются соглашениями. В физике и ее технических приложениях меры получили название физических величин. К ним относятся длина, сила, масса, давление, время, скорость и др. В математике: мера рассеивания значений случайной величины – дисперсия; в информатике мера неопределенности – энтропия. В экономике мерами служат экономические показатели. Это стоимость, прибыль, цена, затраты и т.д. В квалиметрии меры называются показателями качества. Можно привести и другие системы мер.
Что такое физическая величина?
Физическая величина – свойство общее в качественном отношении многим физическим объектам, но в количественном отношении индивидуальное для каждого объекта. Индивидуальность в количественном отношении понимают в том смысле, что свойство может быть для одного объекта в определенное число раз больше или меньше, чем для другого. Таким образом, физическая величина – это измеренные свойства или характеристики физических объектов или процессов, с помощью которых они могут быть изучены, т. е. найдены свойственные им закономерности. К физическим величинам относятся: длина, масса, время и т. д.
В физике рассматривается большое число величин, для каждого ее раздела характерны свои величины, однако некоторые из них являются общими для различных разделов физики, например, энергия, могущая переходить из одной формы в другую.
Вместе с этим в технике приходится оперировать с большим числом величин, не являющихся непосредственно физическими величинами, но позволяющих оценивать с количественной стороны различные технические устройства.
Величины можно характеризовать своим видом, определяющим качественную сторону, и размером, т. е. количественной стороной. Вид величины это только ее характер без указания, к какому объекту она относится. Так, длина вообще, масса вообще. При измерениях же мы имеем дело с конкретными объектами, с которыми связана величина. Например, объектом измерений может быть диаметр втулки (как частный случай длины), количество зерна в бункере (как частный случай массы) и множество других величии, связанных с самыми разнообразными объектами.
Размер величины всегда выражается некоторым числом принятых единиц измерений.
Что понимают под термином размерность физической величины?
Формализованным отражением качественного различия физических величин является их размерность. Размерность обозначается символом dim, происходящим от слова dimension, которое в зависимости от контекста может переводиться и как размер, и как размерность.
Размерность основных физических величин обозначается соответствующими заглавными буквами. Для длины, массы и времени, например,
dim l = L; dim m = M; dim t = Т.
При определении размерности производных величин руководствуются следующими правилами:
1. Размерности правой и левой частей уравнения не могут не совпадать, т.к. сравниваться между собой могут только одинаковые свойства. Таким образом, алгебраически могут суммироваться только величины, имеющие одинаковые размерности.
2. Алгебра размерностей мультипликативна, т.е. состоит из одного единственного действия - умножения.
2.1. Размерность произведения нескольких величин равна произведению их размерностей. Так, если зависимость между значениями величин Q, А, В, С имеет вид Q=АВС, то
dim Q = dim A×dim В×dim С.
2.2. Размерность частного при делении одной величины на другую равна отношению их размерностей, т.е. если Q=A/B , то
dim Q = dim A / dim В.
2.3. Размерность любой величины, возведенной в некоторую степень, равна ее размерности в той же степени. Так, если Q=An, то
dim Q =
![]() dim A = dimnA.
dim A = dimnA.
Например, если скорость определять по формуле V = S/t, то
dim V = dim S/dim t = L/T=LT-1.
Если сила по второму закону Ньютона F = ma, где a = V/t - ускорение тела, то
dim F = dim m dim a = ML/T2 = MLT-2.
Таким образом, всегда можно выразить размерность производной физической величины через размерности основных физических величин с помощью степенного одночлена:
dim Q = LaMbTg,
где L, М, Т, - размерности соответствующих основных физических величин; a, b, g, - показатели размерности. Каждый из показателей размерности может быть положительным или отрицательным, целым или дробным числом, нулем.
Если все показатели размерности равны нулю, то такая величина называется безразмерной. Она может быть относительной, определяемой как отношение одноименных величин (например, относительная диэлектрическая проницаемость), и логарифмической, определяемой как логарифм относительной величины (например, логарифм отношения мощностей или напряжений).
Теория размерности повсеместно применяется для оперативной проверки правильности формул (по правилу 1). Формальное применение алгебры размерностей иногда позволяет определить неизвестную зависимость между физическими величинами.
Что такое единица измерений физической величины?
Единица измерений физической величины есть физическая величина фиксированного размера, которой условно присвоено числовое значение равное единице, и применяемая для количественного выражения однородных с ней физических величин. Единицы измерений некоторой величины могут отличаться по своему размеру, например, метр, фут и дюйм, являясь единицами длины, имеют различный размер: 1 фут = 0,3048 м, 1 дюйм = 0,254 м.
Какие утверждения лежат в основе теоретической метрологии?
В теоретической метрологии приняты три постулата, которыми руководствуются на трех этапах метрологических работ:
- при подготовке к измерениям (постулат 1);
- при проведении измерений (постулат 2);
- при обработке измерительной информации (постулат 3).
Постулат 1: без априорной информации измерение невозможно.
Постулат 2: измерение есть ни что иное, как сравнение.
Постулат 3: результат измерения без округления является случайным.
Что такое априорная измерительная информация?
Априорной измерительной информацией является вся сумма знаний об измеряемом объекте и условиях проведения измерений, которой располагают до начала измерений. Действительно, если об исследуемом объекте мы ничего не знаем, то не можем начать измерение; неизвестно, что измерять, каким образом и каким средством измерений измерять и с какими величинами сравнивать.
Если об исследуемом объекте известно все, то измерение не нужно: оно не даст никакой дополнительной информации. Таким образом, измерение обусловлено дефицитом количественной информации о том или ином свойстве объекта или явления и направлено на его уменьшение.
Что нужно знать об измеряемом объекте до начала измерений?
Экспериментатор должен иметь априорную информацию об измеряемом объекте по сданным направлениям:
- уровень контролепригодности измеряемого параметра: возможно ли, в принципе, проведение измерений этого параметра имеющимися средствами измерений?
- единицы величин, в которых надо измерять параметр, т.е. с чем сравнивать его размер?
- возможный диапазон изменения измеряемой величины ля определения диапазона измерений выбираемых технических средств;
-
возможные. влияющие на результат измерения, факторы с целью их исключения, учета или компенсации.
Почему результат измерений является случайной величиной?
Любой результат измерений содержит погрешность из-за наличия погрешностей, присущих средству измерений, методу и методике измерений, из-за влияния внешних факторов и других причин, вызывающих погрешности.
Рассеяние результатов, проявляющееся в несовпадении результатов измерений одной и той же величины в ряду равноточных измерений, как правило, обуславливается наличием случайных погрешностей. В этом случае количественную оценку рассеяния результатов в ряду измерений вследствие действия случайных погрешностей обычно получают после введения поправок на действие систематических погрешностей. Оценками рассеяния результатов в ряду измерений являются: размах, средняя арифметическая погрешность (по модулю), средняя квадратическая погрешность (стандартное отклонение), доверительные границы погрешности.
Как известно, случайные погрешности прогнозировать, исключать или компенсировать невозможно. Вследствие неизбежного содержания случайных погрешностей результаты измерений рассматриваются как случайные величины. Поэтому при статистической обработке результатов измерений наиболее полными являются их вероятностные характеристики.
Что такое общее уравнение измерений?
Суть измерения заключается в количественном выражении искомой величины (на основании эксперимента) с помощью сопоставления этой величины с однородной величиной, принятой за единицу. Результат измерения записывается в виде общего уравнения измерений:
Q = n[Q], (1)
где Q – измеряемая физическая величина; п – число единиц; [Q] – единица физической величины.
Что представляет собой система единиц физических величин?
Система единиц физических величин - совокупность основных и производных единиц физических величин, образованная в соответствии с принципами для заданной системы физических величин. Например, Международная система единиц (СИ), принятая в 1960 г.
Основная единица системы единиц физических величин - единица основной физической величины в данной системе единиц. Например, основные единицы Международной системы единиц: метр (м), килограмм (кг), секунда (с), ампер (А), кельвин (К), моль (моль) и кандела (кд).
Определение понятия "дополнительная единица" в международных документах отсутствует. До введения Международной системы единиц СИ это понятие в физике не применялось. В СИ единицы плоского (радиан) и телесного (стерадиан) углов выделены в отдельную группу дополнительных единиц, хотя определение, что понимается под дополнительными величинами и, соответственно, единицами не дано.
Производная единица системы единиц физических величин - единица производной физической величины системы единиц, образованная в соответствии с уравнением, связывающим ее с основными единицами или же с основными и уже определенными производными.
Что такое производные единицы СИ?
Производные единицы СИ образуются из основных, дополнительных и ранее образованных производных единиц СИ при помощи уравнений связи между физическими величинами, в которых числовые коэффициенты равны единице. Для этого величины в правой и левой частях уравнения связи принимают равными единицам СИ. Например, для производной единицы скорости СИ, определяемой из уравнения v = L/T записывают уравнение единиц [v] = [L] /[T], а вместо символов Lи T подставляют их единицы (1 м и 1 с) и получают [V]=1 м/1 с = 1 м/с. Это означает, что единицей скорости СИ является метр в секунду.
Производным единицам могут присваиваться наименования в честь известных ученых.
Так, уравнение связи между величинами для определения единицы давления p=F/S, уравнение связи между единицами давления, силы и площади [р]= [F]/[S]. Подставив вместо F и S единицы этих величин в СИ (1 Н и 1 м2), получим [р]=1 н/ 1 м2 = 1 Н/м2. Этой единице присвоено наименование – паскаль (Па) по имени французского математика и физика Блеза Паскаля.
Каковы принципы формирования и виды систем единиц?
Принципы формирования систем единиц физических величин были сформулированы К. Гауссом в 1832 г.:
1) выбираются основные физические величины;
2) устанавливаются единицы основных физических величин; Размеру каждой основной физической величины приписано числовое значение, равное единице. Выбор его является произвольным и определяется только удобством применения. Эти размеры, называемые единицами основных физических величин, закрепляются законодательным путем;
3) устанавливают единицы производных физических величин.
К. Гауссом была разработана система единиц, названная им абсолютной, с основными единицами – миллиметр, миллиграмм и секунда. Ученый В. Вебер распространил предложенный К. Гауссом метод образования производных единиц на электрические величины {электродвижущую силу, силу тока, сопротивление).
Метод, указанный Гауссом и Вебером, был в последующем применен для построения электростатической и электромагнитной систем СГС (сантиметр, грамм, секунда), принятых комиссией Британской ассоциации для развития наук. Число систем единиц продолжало увеличиваться и в результате было создано и внедрено в практику довольно много различных систем, основанных на метрических единицах, например в области механики:
Сантиметр – грамм – секунда (СГС),
метр – тонна – секунда (МТС),
метр – килограмм – секунда (МКС),
метр– килограмм-сила – секунда (МКГСС).
В области электродинамики:
сантиметр – грамм – секунда электростатическая (СГС Е),
сантиметр – грамм – секунда электромагнитная (СГС М)
сантиметр – грамм – секунда симметрическая или Гауссова (СГС).
Кроме этих, находили широкое применение и другие системы – МКСА, МКГСС, МКСГ и др.
Из приведенных примеров о развитии систем единиц, видно, что в этом развитии не было общего, объединяющего принципа. Единицы зачастую подбирали для отдельно взятых групп величин. Это и приводило к большой пестроте единиц и затрудняло обеспечение единства измерений.
В настоящее время при построении или введении новой системы единиц ученые руководствуются только практической целесообразностью, для обеспечения которой существуют критерии:
- простота образования производных физических величин и их единиц, т.е. равенство единице коэффициентов пропорциональности в уравнениях связи (свойство когерентности);
- высокая точность материализации основных и производных единиц и передачи их размера нижестоящим эталонам;
- неуничтожаемость эталонов основных единиц, т.е. возможность их воссоздания в случае утраты;
- преемственность единиц, сохранение их размеров и наименований при введении новой системы единиц, что снижает материальные и психологические затраты;
- близость размеров основных и производных единиц к размерам физических величин, наиболее часто встречающихся на практике;
- долговременность хранения основных и производных единиц их эталонами;
- выбор в качестве основных минимального числа физических величин, отражающих наиболее общие свойства материи.
Как появилась и развивалась метрическая система единиц?
7 апреля 1795 года Конвент Франции принял закон о введении метрической системы мер, в которой первой из основных единиц была единица длины – метр. В 1799 г. Парижской академией наук была закончена работа по созданию платиновых прототипов метра и килограмма. Они сданы на хранение в Архив Франции и называются архивными.
20 мая 1875 г. В Париже представителями 17 государствам была подписана Метрическая конвенция для обеспечения международного единства и усовершенствования метрической системы мер.
В России метрическая система мер была официально признана и применялась как предпочтительная с подписанием декрета Совнаркома РСФСР от 14 сентября 1918 г. С 1 января 1927 г. Эта система стала единственной допускаемой в СССР.
В результате развития метрической системы мер возникла множественность единиц измерений, вошедших в употребление в науке и технике, ставшей препятствием для сопоставления результатов измерений данных о свойствах веществ и материалов, для выполнения технических расчетов, т. е. она стала препятствием для прогресса науки и техники. Так появилась потребность замены множественности применяемых единиц одной унифицированной системой единиц.
В 1954 г. Х Генеральной конференцией по мерам и весам принято решение о применении в качестве основных единиц практической системы: длины – метр, массы – килограмм, времени – секунда, силы тока – ампер, термодинамической температуры – градус Кельвина, силы света – кандела (свеча).
Что представляет собой система единиц SI (СИ)?
В 1960 г. XI Генеральная конференция по мерам и весам приняла список двух дополнительных и 27 производных единиц и присвоила ей наименование «Международная система единиц». Сокращенное обозначение SI (от начальных букв SI в словах System International). На XIV Конференции была введена седьмая основная единица СИ – моль.
Внедрение Международной системы единиц в нашей стране осуществлялось в несколько этапов, а окончательно сформировалась СИ с 1 января 1982 г. С этого времени был внедрен ГОСТ 8.417—81 (СТ СЭВ 1052—78) «ГСИ. Единицы физических величин». Все другие системы с этого времени подлежали изъятию.
Основные достоинства СИ:
- универсальность – охват всех областей науки и техники;
- унификация единиц для всех областей и видов измерений (механических, тепловых, электрических, магнитных и т. д.), например, вместо ряда применявшихся ранее единиц работы и энергии (кгс-м, эрг, л.с-ч., кал, Вт-с, Дж и другие) в СИ предусмотрена одна системная единица джоуль (Дж), как единица работы, энергии, количества теплоты;
- когерентность единиц – все производные единицы СИ получаются из уравнений связи между величинами, в которых коэффициенты равны единице;
- возможность воспроизведения единиц с высокой точностью в соответствии с их определениями.
- упрощение записи уравнений и формул в физике, химии, а также в технических расчетах в связи с отсутствием переводных коэффициентов;
- уменьшение числа допускаемых единиц;
- единая система образования кратных и дольных единиц, имеющих собственные наименования;
- облегчение процесса обучения.
В настоящее время СИ состоит из 7 основных, 2 дополнительных и ряда производных единиц.
Что представляют собой основные единицы системы СИ?
Основными единицами Международной системы СИ являются: метр, килограмм, секунда, ампер, градус Кельвина, канделла, моль. При выборе этих единиц руководствовались только практической целесообразностью, т.е. удобством применения единиц в деятельности человека.
Метр – единица длины, равная пути, проходимому в вакууме сетом за 1/299792458 долю секунды. Первоначально метр был определен как длина 1/40000000 доли длины Парижского меридиана и воспроизводился как расстояние между рисками, нанесенными на платиновом, а позднее платиноиридиевом брусе Х-образного сечения. Но эта величина оказалась нестабильной, поэтому метр стали выражать с помощью длины волны излучения красной линии кадмия, а в настоящее время – оранжевой линии излучения атома криптона-86. 1 метр соответствует 1650763,73 длин волн излучения в вакууме, соответствующего переходу между уровнями 2p10 и 5d5 атома Kr-86.
Метр определяют косвенными методами на радиометрических мостах. Они состоят из ряда последовательно расположенных радиотехнических генераторов и лазеров с умножением частоты между ними. На вход подается эталонная частота 5 Мгц от генератора, синхронизированного через систему умножителей частоты с водородными генераторами эталона времени и частоты, откалиброванными по цезиевому реперу частоты. Мост умножает эту частоту до значения около 1*1014 Гц. Задача его – измерять частоты стабилизированных лазеров. Зная их, вычисляют длины волн их излучения и с помощью оптических интерферометров аттестуют и поверяют различные меры длины.
Килограмм – единица массы, равная массе 1,000028 дм3 воды при температуре ее наибольшей плотности 4 ºС.
Эталоны кг в России представляет собой цилиндр высотой и диаметром по 39 мм с закругленными ребрами. Ведутся работы по определению килограмма через Вольт и Ом с помощью обращенных ампер-весов.
Секунда – единица времени, равная 9192631770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133. Эталон секунды установлен в 1967 г.
Эталон секунды основан на способности атомов излучать и поглощать энергию во время перехода между двумя энергетическими состояниями в области радиочастот. Репер, или квантовый стандарт частоты, представляет собой устройство для точного воспроизведения частоты электромагнитных колебаний в сверхвысокочастотных и оптических спектрах, основанное на измерении частоты квантовых переходов атомов, ионов или молекул. В пассивных квантовых стандартах используются частоты спектральных линий поглощения, в активных – вынужденное испускание фотонов частицами. Применяются активные квантовые стандарты частоты на пучке молекул аммиака (так называемые молекулярные генераторы) и атомов водорода (водородные генераторы). Пассивные стандарты частоты – на пучке атомов цезия (цезиевые реперы частоты)
Для воспроизведения секунды используются цезиевые генераторы (эталоны) частоты – это высокостабильные генераторы монохроматического излучения (сигнала) с частотой 9192631770 Гц; погрешность частоты не превышает 1,5*10 -13. В государственном эталоне России используются водородные генераторы периодически сличаемые с цезиевыми, их долговременная частота не постулирована, но нестабильность меньше 3*10 -14. кроме того эталон содержит аппаратуру формирования и хранения шкал времени. Основная шкала – равномерного атомного времени ТА с фиксированным О, не связанным с вращением и положением в пространстве земли. Другие шкалы: UT0 – всемирного времени (средняя солнечная «с» ); UT1 с поправкой на колебания полюсов земли; UT2 – на сезонную неравномерность вращения земли. Это всемирные шкалы, постепенно расходящиеся с ТА из-за замедления скорости вращения земли. Чтобы их согласовать введена UTC, в которой 1с utc=1с та, а начало счета может меняться на 1с с 1-го числа каждого месяца (1.01 или 1.06) В России UTC-SU- сигналы времени по TV или радио.
Ампер – единица силы электрического тока. Ампер равен силе неизменяющегося тока, который проходя по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызывал бы на каждом участке проводника длиной 1 м силу взаимодействия, равную 2·10-7 Н.
В качестве эталонов Ампера используются либо ампер-весы, реализующие А путем измерений силы, либо путем измерения момента силы, действующем катушку с током, помешенную в магнитное поле другой катушки. Это точные равноплечие весы, выполненные из немагнитных материалов. На одном конце коромысла подвешена чашка для размещения постоянного и дополнительного уравновешивающих грузов. К другому концу коромысла подвешивается подвижная катушка, входящая коаксиально в неподвижную катушку большего диаметра. Обмотки катушек (в простейшем случае) соединены последовательно. В обесточенном режиме весы уравновешиваются. При прохождении через катушки электрического тока подвижная катушка втягивается в неподвижную (или выталкивается из нее ). Для восстановления равновесия служит дополнительный уравновешивающий груз. По результатам метрологического исследования рассчитывают значение массы этого груза, соответствующего, например, силе электрического тока 1А, включив в цепь катушек эталонный резистор, можно откалибровать эталонные меры ЭДС (эталонные меры силы тока пока не применяются).
Более точные эталоны, основанные на измерениях магнитной индукции методом ядерного магнитного резонанса, используются пока только в качестве вторичных. В 1992 г. в России утвержден национальный эталон А, размер которого воспроизводится с использованием элементов вольта и Ома.CKO≤1·10-8, HCП≤1·10 -7 (у ампер-весов CKO≤4·10-6, HCП≤8·10-6).
Кельвин – единица термодинамической температуры, равная 1/273,16 части термодинамической температуры тройной точки воды. Тройная точка воды – это состояние воды в запаянном стеклянном сосуде, при котором лед, вода и ее пары находятся в равновесии: вода не замерзает, не испаряется, лед не тает, пар не конденсируется.
Государственные первичные эталоны России воспроизводят МГШ-90 в двух поддиапазонах: 0,8…273,16 К и 373,16…2773 К. В состав низкотемпературного эталона в качестве основной его части входят две группы железно-родиевых и платиновых термометров сопротивления, градуировочные зависимости которых определены по результатам сличений результатов лаборатории России, Англии, США, Австралии и Голландии. Каждая группа содержит 2 платиновых и 2 железно-родиевых термометра, постоянно находящихся в блоке сравнения – массивном цилиндре с четырьмя продольными каналами для термометров. Передача шкалы термометром – вторичным и рабочим эталонами осуществляется приведением их в тепловой контакт с эталонным блоком сравнения и сличением в криостате. В набор контрольной аппаратуры эталона помимо устройств для точных измерений сопротивлений входит комплект установок для реализации температур реперных точек, газовый интерполяционный термометр с уникальным ртутным манометром и криостат сравнения; СКО эталона 0,3…1,0 мК, НСП 0,4…1,5 мК. Наименьшее значение 0,8К.
В состав второго эталона входят платиновые термометры сопротивления, температурные лампы, аппаратура воспроизведения реперных точек в диапазоне 273,16…1355,77 К, (СКО≤5·10-5...1·10-2; НСП≤1·10-45…10-3)
Шкала Цельсия: °С=К=tС+273,16
Шкала Реомюра:1°R=1,25 °C; tС=1,25 tR; T=1,25 tR+273,16
Шкала Фаренгейта: 1°F=5/9°C=5/9K; tС=5/9( tF-32); T=5/9( tF-32)+273,16
Канделла – единица силы света, равная силе света в заданном направлении источника, испускающего монохроматическое излучение частотой 540·1012 Гц, энергетическая сила света которого в этом направлении составляет 1/683 ВТ/ср. Инициаторами введения этой единицы были астрономы. В государственном эталоне свет испускается с определенной поверхности затвердевающей платины при определенных внешних условиях и воспринимается первичным фотометром, созданным на основе неселективного радиометра, спектральная чувствительность которого скоррелирована на специальном фильтре под функцию V(λ). Эталон воспроизводит единицу силы света в диапазоне 30…110 кд с СКО≤0,1·10-2 и НСП≤0,25·10-2.
Моль – единица количества вещества, равная количеству вещества, содержащему столько же структурных элементов (атомов, молекул), сколько их содержится в 0,012 кг углерода-12. Никогда не создавались эталоны моля, так как масса одного моля различных веществ или структур, численно равная числу Авогадро – 6,025·1023 частиц; СИ, отградуированных в молях, не выпускаются. Есть обоснованные предложения исключить моль из основных единиц СИ и допустить его к применению наравне с единицами СИ как специальную единицу массы, удобную для химических расчетов.
Эталонная база России имеет 114 государственных эталонов и более 250 вторичных эталонов единиц ФВ. Из них 52 находятся во ВНИИМ им. Д.И.Менделеева (С.-П.), в т.ч. эталоны м, кг, А, К, рад; 25 – во ВНИИФТРИ (физико-технических и радиотехнических измерений, г.Москва, в т.ч. эталоны единиц времени и частоты; 13 – во ВНИИ оптико-физических измерений в т.ч. канделлы; соответственно 5 и 6 – в Уральском и Сибирском НИИ метрологии.
Что такое кратные и дольные единицы,
и каковы правила их образования?
На XI Генеральной конференции по мерам и весам вместе с принятием СИ были приняты 12 кратных и дольных приставок, к которым на последующих конференциях были добавлены новые. Приставки дали возможность образовывать десятичные кратные и дольные единицы от единиц СИ.
Кратная единица физической величины - единица физической величины, в целое число раз большая системной или внесистемной единицы. Например, единица длины 1 км = 103 м, т. е. кратная метру; единица частоты 1 МГц (мегагерц) = 106 Гц, кратная герцу; единица активности радионуклидов 1 МБк (мегабеккерель)=106Вк, кратная беккерел.
Дольная единица физической величины - единица физической величины, в целое число раз меньшая системной или внесистемной единицы.
Названия кратных и дольных единиц образуются с помощью приставок, приведенных в таблице.
Таблица 1 – Множители и приставки к единицам СИ
|
Множитель |
Название |
Происхождение |
|
1018 1015 1012 109 106 103 102 101 10-1 10-2 10-3 10-6 10-9 10-12 10-15 10-18 |
экса пета тера гига мега кило гекто дека деци санти танц микро нано пико фемто атто |
шесть (раз по 103) пять (раз по 103) огромный гигант большой тысяча сто десять десять сто тысяча малый карлик пикколо (маленький) пятнадцать восемнадцать |
Каковы правила образования кратных и дольных единиц?
14.
Присоединение подряд двух или более приставок к исходной единице не допускается
Неправильно Правильно
микрокилограмм миллиграмм
2. Приставку или ее обозначение пишут слитно с наименованием единицы или с ее обозначением
Неправильно Правильно
деци-метр дециметр
3. К единице, образованной произведением или отношением единиц присоединяют приставку по наименованию первой единицы. Например, для единицы — паскаль-секунда на метр (Па с/м)
Неправильно Правильно
паскаль-килосекунда на килопаскаль-секунда на метр
метр (Па кс/м) (кПа с/м)
Для ряда единиц, имеющих широкое применение, приставка может применяться во втором сомножителе. Например, ватт на квадратный сантиметр (Вт/см2).
4. Если единицы возведены в степень, то приставку присоединяют к наименованию исходной единицы. Например, приставку «кило» для единицы объема (кубический метр) присоединяют к слову метр, в результате образуется кратная единица — кубический километр.
5. Выбор десятичной кратной или дольной единицы диктуется удобством ее применения Обычно выбирают ту единицу, которая приводит к числовым значениям, приемлемым на практике. Обычно их выбирают таким образом, чтобы числовое значение измеряемой величины было в диапазоне от 0,1 до 1000.
6. В случае, когда наименование производной единицы представляет собой произведение единиц, то оно записывается через дефис, до и после которого не оставляется пробел — ньютон-метр (Нм) и др. Если же в наименовании производной содержится отношение единиц, то используется предлог «на» — ампер на метр (А/м) и др. Исключение составляют единицы, характеризующие явления во времени. Для них используется предлог «в» – метр в секунду (м/с) и др.
7. При склонении сложных наименований, представляющих собой произведение единиц, склоняется только последнее наименование и относящееся к нему прилагательное «квадратный», «кубический», например, магнитный момент равен пяти ампер-квадратным метрам. При склонении наименований, представляющих собой отношение единиц, склоняется только числитель, например, теплопроводность равна – 10 ваттам на метр-кельвип и др.
8. В наименованиях единиц площади и объема применяются прилагательные «квадратный» и «кубический» – квадратный метр (м2) и др. Эти же прилагательные применяются в случаях, когда единица площади или объема входит в производную единицу другой величины – кубический метр в секунду (м3с) и др.
Если же вторая и третья степени длины не представляют собой площади или объема, то в наименовании единицы применяются выражения «в квадрате» или «во второй степени», «в кубе» или «в третьей степени» – килограмм-метр в квадрате (кг-м2) и др.
9. Международные и русские обозначения относительных и логарифмических единиц: процент (%), промилле (%о), миллионная доля (ррт, млн-1), бел (В, Б), децибел (dB, дБ), октава (окт), декада (дек), фон (phon, фон).
10. К обозначениям единиц и их наименованиям нельзя добавлять буквы (слова), указывающие на физическую величину или на объект. Например, п. м. или мп (погонный метр), укм (условный квадратный метр), экм (эквивалентный квадратный метр), нм3 или Нм3 (нормальный кубический метр), тут (тонна условного топлива), % весовой (весовой процент). Во всех таких случаях определяющие слова следует присоединять к наименованию величины, а единицу обозначать в соответствии со стандартом. Например, погонная длина 10 м, эквивалентная площадь 40 м2, объем газа (приведенный к нормальным танцииям) 300 м3, масса топлива (условного) 7000 т, массовая доля 30 %, объемная доля 5 % и т д.
Обозначения единиц, названных в честь ученых, пишут с прописной буквы (А,К,Ф и др.)
Буквенные обозначения единиц печатаются прямым шрифтом. В обозначениях единиц точка в качестве знака сокращения не ставится. Однако если сокращается слово, входящее в наименование единицы, то точка ставится. Например, мм рт. Ст. Буквенные обозначения единиц, входящих в произведение, танцииются точками на средней линии как знаками умножения, однако это не касается машинописных текстов Нельзя при указании производной единицы, состоящей из двух и более единиц, для одних приводить обозначения, а для других наименования. Вместе с тем в обоснованных случаях допускается использовать сочетания специальных знаков с буквенными обозначениями единиц.
11. Если в числовом значении величины встречается десятичная дробь, обозначение единицы ставится после всех цифр. Если указаны значения величины с допусками (предельными отклонениями) , следует заключить числовые значения в скобки и обозначения единиц помещать после скобок или проставлять обозначения единиц после числового значения величины и после ее предельного отклонения
Правильно Неправильно
(100,0±0,1) кг 100,0±0,1 кг
50 г±1 г 50±1 г
Если в тексте приводят подряд несколько числовых значений какой-нибудь физической величины, выраженных одной и той же единицей, эту единицу можно указывать только после последней цифры.
12. В случае, когда производные единицы образованы путем деления одних на другие, то в их обозначениях должна применяться косая черта, при этом сами обозначения помещаются в строку. При использовании косой черты обозначения произведения единиц в знаменателе должны быть заключены в скобки. Допускается обозначение единицы в форме произведения обозначений единиц, возведенных в положительные и отрицательные степени, а также с помощью пробной черты. Нельзя при обозначении сложных производных единиц применять более одной косой или горизонтальной черты. Обозначения единиц, совпадающие с наименованиями этих единиц, по падежам и числам изменять не следует, если они помещены после числовых значений, а также в заголовках граф, боковиков таблиц и выводах, в пояснениях обозначений величин к формулам.
К таким обозначениям относятся: бар, та, вар, моль, рад. Следует писать: 1 моль, 2 моль, 5 моль и т. Д. Исключение составляет обозначение: «св. год», которое изменяется следующим образом 1 св. год, 2, 3, 4 св. года, 5 св. лет.
13. При образовании и обозначении кратных и дольных единиц следует помнить, что если физическая величина имеет наименование из одного слова, то приставка пишется слитно с наименованием. Нельзя применять две и более приставок.
Правильно Неправильно
ГДж МкДж
В связи с тем, что наименование основной единицы массы килограмм — содержит приставку «кило», для образования кратных и дольных единиц массы используют дольную единицу – грамм.
Правильно Неправильно
мг мккг
В случае, когда единица образована как произведение или отношение единиц, приставку следует присоединить к наименованию первой единицы, входящей в произведение или отношение
Правильно Неправильно
кПа с/м Па кс/м
Приставку можно применять во втором множителе или знаменателе в обоснованном случае, когда имеется широкое распространение таких единиц. Например, Bт/см2, А/мм2.
14. Наименования кратных и дольных единиц от единицы, возведенной в степень, следует образовывать путем присоединения приставки к наименованию исходной единицы. Обозначения кратных и дольных единиц oт единицы, возведенной в степень, следует образовывать добавлением соответствующего показателя степени к обозначению кратной или дольной этой единицы, причем, показатель обозначает возведение в степень кратной или дольной единицы вместе с приставкой.
Например, 0,02 см-1= 0,02 (10-2 м) =0,02.100 м-1 =2 м-1.
Что такое внесистемные единицы?
Система единиц и сами единицы складывались веками, образовывались определенные традиции и привычки. Так, до недавнего времени урожайность в нашей стране определялась в миллионах пудов, в США используют единицу массы фунт, единицу длины — милю и т.д.
В то же время эти и другие единицы не входят в СИ и тем не менее они используются в науке и технике, в быту.
Внесистемные единицы, допускаемые к применению наравне с единицами СИ, соответствуют 10 физическим величинам Для некоторых величин имеется несколько единиц, поэтому общее число достигает 18. Внесистемные единицы подразделяются на два вида:
- единицы, получившие распространение наравне с единицами СИ и в сочетании с ними;
- единицы, применяемые в специальных областях науки и техники.
Примечание. Не допускается применение с приставками единиц времени (минута, час, сутки) и плоского угла (радиус, минута, секунда).
Внесистемные единицы, временно допускаемые к применению, подлежат постепенному изъятию в соответствии с решениями международных организаций в том или ином виде деятельности. Например, традиционно использующаяся единица длины — миля и единица скорости — узел применяются в морской навигации всех стран. Морские карты, приборы выпускаются и используются с учетом этих единиц. Переход на единицы СИ возможен лишь в будущем.
Примечание. Не допускается применение с приставками следующих единиц: астрономическая, световой год, диоптрия, атомная единица массы.
Что такое измерение?
Измерение физических величин представляет собой совокупность операций по применению технического средства, хранящего единицу физической величины и обеспечивающего нахождение соотношения (в явном и неявном виде) измеряемой величины с ее единицей и получение значения этой танциины.
Результат измерения записывается в виде общего уравнения измерений:
Q = n [Q],
где Q – измеряемая физическая величина; п – число единиц; [Q] – единица физической величины.
Примечание. Так как измеряются не только физические величины, имеет место и другая трактовка понятия «измерение». Измерение – совокупность операций, выполняемых с целью определения значение величины. Здесь определение понятия «измерение» не ограничивается нахождением значения танцческой величины, нет упоминания о технических средствах. Данная трактовка понятия подходит как к физическим, так и нефизическим величинам. Следовательно, к измерениям можно отнести и различные виды количественного оценивания величин.
Что такое единство измерений?
Единство измерений – это состояние измерений, характеризующееся тем, что их результаты выражаются в узаконенных единицах, размеры которых в установленных пределах равны размерам единиц воспроизводимых первичными эталонами, а погрешности результатов измерений известны и с заданной вероятностью не выходят за установленные пределы. Таким образом, для обеспечения единства измерений все должны пользоваться при измерениях одинаковых физических величин одинаковыми единицами измерений.
Единство измерений достигается точным воспроизведением и хранением установленных ЕФВ и передачи их размеров применяемым СИ. Это осуществляется с помощью эталонов калибровкой и испытаниями средств измерений на предприятиях изготовителях и периодичности поверки или калибровки при эксплуатации на определения соответствия МХ, установленным в НД на них нормам. Если эти нормы нарушены, СИ изымается из эксплуатации и после ремонта заново градуируется, калибруются, поверяются.
Как классифицируются измерения?
В зависимости от характерных признаков, измерения классифицируются на несколько видов:
·
по характеристике точности – равноточные, неравноточные;
·
по числу измерений в серии – однократные и многократные;
·
по выражению результата измерений – абсолютные и относительные;
·
по отношению к изменению измеряемой величины во времени – статические и динамические;
·
по метрологическому назначению – технические и метрологические;
·
по общим приемам получения результатов измерений – прямые, косвенные, совместные, совокупные.
Что такое равноточные и неравноточные измерения?
Равноточные измерения – ряд измерений какой-либо величины, выполняемых одинаковыми по точности средствами измерений в одних и тех же условиях с одинаковой тщательностью.
Неравноточные измерения – ряд измерений какой-либо величины, выполненных различающимися по точности средствами измерения, в разных условиях и (или) разными операторами.
Зачастую измерения требуют много времени, в течение которого не всегда удается сохранить идентичность условий измерений. Меняющиеся условия измерений, вынужденная замена одних средств измерений другими, смена оператора – все это приводит к получению групп измерений с разными характеристиками погрешностей. Такие группы измерений и называют неравноточными. К ним также относят и группы измерений, в которых измерение одной и той же величины производится разными методами, характеризующимися различными погрешностями.
Что такое однократные и многократные измерения?
Однократное измерение — измерение, выполненное один раз.
Например, определение времени по часам. При таких измерениях показания средств измерений являются результатом измерений, а погрешность используемого средства измерений определяет погрешность результата. Поэтому перед проведением измерений принимают меры по созданию и поддержанию нормальных условий, т. Е. определяются влияющие факторы и меры, направленные на уменьшение их влияния, значения поправок, выбирается средство измерений, изучаются его метрологические характеристики. Одним из главных итогов этой работы должна быть уверенность в том, что погрешности метода и оператора малы по сравнению с допускаемой погрешностью измерений (обычно допускается их сумма не свыше 30% от допускаемой погрешности измерений). Если это условие выполняется, то в результате измерения получают одно значение отсчета, которое используется для получения единственного значения Q измеряемой величины (результата измерений). Однократные измерения используют в тех случаях, когда случайная составляющая погрешности мала по сравнению с не исключенными систематическими погрешностями, или в тех случаях, когда для их проведения есть производственная необходимость, т.е. условия измерений не позволяют провести повторные измерения.
Если необходима большая уверенность в получаемом результате, то проводятся многократные измерения.
Многократное измерение – измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, т. Е. состоящее из ряда однократных измерений (выполненных не менее 4 раз).
За результат многократного измерения обычно принимают среднее арифметическое значение из результатов однократных измерений, входящих в ряд.
Эти измерения повторяются оператором в одинаковых условиях, использующим одни и те же средства измерений. Такие измерения характерны при выполнении метрологических работ, а также находят широкое применение в научных исследованиях. По результатам многократных измерений проводится анализ, главной особенностью которого является получение и использование большого объема измерительной информации.
Прежде чем приступить к обобщению результатов измерений, определяют, нет ли в полученных результатах грубых погрешностей.
Применение многократных измерений позволяет повысить точность измерения до определенного предела, но недостаток полученной информации не позволяет получить точное значение поправок, значений составляющих погрешностей и т.п. В связи с этим устанавливают необходимое число измерений, которое позволяет получить результат измерений, в котором случайная погрешность пренебрежимо мала по сравнению с неисключенной систематической погрешностью. Число измерений находят по формуле n = 64(s/q) где s – среднее квадратическое отклонение ряда измерений, q – неисключенная систематическая погрешность.
Что такое абсолютное и относительное измерения?
Абсолютное измерение – измерение, основанное на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант. Абсолютное измерение приводит к значению измеряемой величины, выраженному в ее единицах.
При измерении длины детали штангенциркулем результат выражается в единицах измеряемых величин (в миллиметрах).
Относительное измерение – вид измерения, при котором измеряется отношение величины к одноименной величине, играющей роль единицы или измерения величины по отношению к одноименной величине, принимаемой за исходную.
Примером может служить измеритель скорости у сверхзвуковых самолетов, показывающий отношение скорости самолета к скорости звука, или указатели расхода бензина в автомобилях.
Что такое статические и динамические измерения?
Статические измерения – это измерения физической величины, принимаемой в соответствии с конкретной измерительной задачей за неизменную на протяжении времени измерения.
Например, измерения размеров деталей при нормальной температуре, влажности почвы, зерна, температуры воздуха, размеров земельного участка и др.
Динамические измерения – это измерения, в процессе которых размер физической величины изменяется с течением времени.
Например, измерения давления и температуры в цилиндре работающего двигателя, тяговых усилий трактора, расстояния до поверхности земли со снижающегося самолета.
Строго говоря, все физические величины подвержены тем или иным изменениям во времени. В этом убеждает применение все более и более танциительных средств измерении, которые дают возможность обнаруживать изменение величин, ранее считавшихся постоянными, поэтому классификация измерений на динамические и статические является условной.
Что такое технические и метрологические измерения?
Технические измерения обычно используются в ходе контроля при изготовлении изделий, технологических процессов. Например, измерение давления пара в котле при помощи манометра. Обычно они выполняются с помощью тбочих средств измерений. Погрешность результата технических измерений определяется характеристиками используемых рабочих средств (измерения, выполняемые в процессе производства на предприятиях, испытательных танциииях, в измерительных лабораториях и т. Д.).
Метрологические измерения предназначаются для воспроизведения единиц физических величин или для передачи их размера рабочим средствам измерений. В ходе их выполнения используются эталоны или образцовые средства измерений.
По условиям, определяющим точность результата, они подразделяются на измерения максимально достижимой точности (эталонные, физических констант и сред, например абсолютного значения ускорения свободного падения) и контрольно-поверочные измерения. Во втором случае погрешность не должна превышать некоторое заданное значение (измерения, выполняемые лабораториями государственных и ведомственных метрологических служб).
Что такое прямые измерения?
Прямые измерения – это измерения, при которых искомое значение физической величины получают непосредственно.
Прямые измерения составляют основу более сложных видов измерений.
К прямым измерениям относятся измерения, результаты которых получают с помощью средства измерения, находящегося под воздействием данной измеряемой величины, проградуированного непосредственно в единицах этой величины. При проведении этих измерений, как правило, не требуется каких-либо вычислений.
Математически прямое измерение может быть представлено в виде
Q=n[Q] Числовое значение п, характеризующее размер величины Q, выраженной в единицах [Q], определяется непосредственно по показаниям мер или измерительных приборов, предназначенных для измерений данной величины Q.
Примером прямых измерений являются измерения длины листа бумаги линейкой, времени при помощи часов, массы при помощи гирь на равноплечих весах, температуры – термометром, силы тока – амперметром и т. Д.
Прямое измерение может также заключаться в однократном применении измерительного прибора с непосредственным отсчетом по нему результата, но может включать и несколько повторных наблюдений с вычислением результата как среднего из нескольких измерений. Для получения результата также может потребоваться умножение отсчета по шкале измерительного прибора на цену деления.
Что такое косвенные измерения?
Косвенные измерения – это измерения, при которых определение искомого значения физической величины производится на основании результатов прямых измерении других физических величин, функционально связанных с искомой величиной.
Результат находят из решения уравнения, выражающего эту зависимость:
Q = f(X, Y, Z, … , W) .(2)
где Q – измеряемая величина; X, Y, Z,…, W – величины, размер которых определяется из прямых измерений.
Например, требуется измерить удельное электрическое сопротивление некоторого материала. Так как приборов для прямых измерений удельного сопротивления нет, его можно измерить только косвенно. Для этого воспользуемся уравнением
![]() , (3)
, (3)
где р – удельное сопротивление; R – электрическое сопротивление; S – площадь поперечного сечения; L – длина образца.
Если измерить длину L, площадь поперечного сечения S и электрическое сопротивление R, то можно вычислить и его удельное сопротивление.
Косвенные измерения достаточно часто встречаются в метрологии, где ими пользуются при воспроизведении единиц. Такие измерения позволяют получать более точный результат, чем прямые. Особенно велика роль косвенных измерений в естественных науках, когда реализация прямых измерений при изучении явлений затруднительна. Например, явления, изучаемые в астрономии, молекулярной и атомной физике и т. Д.
Примеры косвенных измерений: определение эффективной мощности двигателя при его испытании на основании прямых измерений крутящего момента и частоты вращения вала двигателя; определение площади фигур или объема тел по прямым измерениям их геометрических размеров.
Что такое совокупные измерения?
Совокупные измерения – это измерения, проводимые одновременно для нескольких одноименных величин, при которых искомые значения величин определяют решением системы уравнений, составляемых по результатам прямых измерений различных сочетаний этих величин.
Для определения значений искомых величин число уравнений должно быть не меньше числа величин. Пример совокупных измерений: массы отдельных гирь набора находят по известной массе одной из них и по результатам прямых сравнений масс различных сочетаний гирь.
Что такое совместные измерения?
Совместные измерения – это проводимые одновременно измерения двух или нескольких не одноименных величин для определения зависимости между ними.
Целью совместных измерений является нахождение функциональной зависимости между величинами (длины тела от температуры, расхода топлива от частоты вращения вала двигателя и т. Д.).
В чем сходства и различия совокупных и совместных измерений?
Система уравнений, получаемая при совместных или совокупных измерениях, может быть записана в виде:
f1=(X1, X2, …, Y11, Y21, …)=0;
f2=(X1, X2, …, Y12, Y22, …)=0;
. . . (4)
fn=(X1, X2, …, Y1n, Y2n, …)=0;
где X1, X2, … – измеряемые величины; Y1n, Y2n – величины, определяемые прямыми или косвенными измерениями.
В данной системе уравнений под величинами X1, X2, …, Y1i, Y2i понимаются конкретные размеры величины, связанные с некоторыми объектами, с которыми имеем дело при данных измерениях. При переходе от одного уравнения к другому изменяются либо условия измерения (при этом группа величин Y11, Y12 … переходят в группу Y12, Y22 Y32 … и т. Д.) в случае совместных измерений, либо сочетания измеряемых величин (т. Е. входящих в группу величин, обозначенных символом X) в случае совокупных измерений.
Совместные и совокупные измерения по способам нахождения искомых значений измеряемых величин близки, так как и в том и в другом случаях они находятся путем решения системы уравнений. Отличие состоит в том, что при совокупных измерениях одновременно измеряют несколько одноименных величин, а при совместных – разноименных.
Совокупные измерения состоят из ряда прямых измерений однородных величин, причем, при переходе от одного ряда к другому меняются сочетания измеряемых величин, из-за чего уравнения, как результаты измерений, могут получиться неравноточными. Например, при определении действительных значений гирь из одного набора для одной гири определяют ее действительное значение путем сравнения с образцовой гирей. А действительное значение остальных гирь находят в результате решения уравнения.
Они построены на основании сравнения в разных сочетаниях всех гирь, входящих в набор.
Совместные измерения основываются на известных уравнениях, отражающих существующие в природе связи между свойствами объектов, т. Е. между величинами.
Например, при установлении зависимости электрического сопротивления катушки от температуры измеряют температуру t и сопротивление катушки R, соответствующее этой температуре. Искомыми величинами являются R20, a, b из формулы
Rt = R20 + a (t-20) + b (t-20)2, (5)
где Rt – сопротивление катушки при температуре t; R20 – сопротивление катушки при температуре 20°С; a и b – коэффициенты температурной зависимости.
Изменяя температуру масла в термостате, в которое погружена катушка сопротивления, определяют прямыми измерениями значения Rt сопротивления катушки и ti ее температуры. В результате получают несколько уравнений вида:
Rt1 = R20 + a (t1-20) + b (t1-20)2,
Rt2 = R20 + a (t2-20) + b (t2-20)2,
. . . (6)
Rtn = R20 + a (tn-20) + b (tn-20)2,
В этих уравнениях роль искомых величин X1, X2, X3 играют R20, a и b, а роль изменяющихся величин Y1i, Y2i, определяемых прямыми измерениями, играют Rti и ti. Вид функций для всех уравнений один и тот же.
Что такое принцип измерений?
Принцип измерений – физическое явление или эффект, положенное в основу измерений.
Например: применение эффекта Джозефсона для измерения электрического напряжения; применение эффекта Пельтъе для измерения поглощенной энергии ионизирующих излучений; применение эффекта Допплера для измерения скорости; использование силы тяжести при измерении массы взвешиванием.
Что такое метод измерений?
Метод измерений – прием или совокупность приемов сравнения измеряемой физической величины с ее единицей в соответствии с реализованным принципом измерений. Метод измерений реализуется устройством средств измерений.
Как классифицируются методы измерений?
Разнообразие измеряемых величин и объектов изучения обуславливает применение большого числа методов измерений и их классификацию.
С точки зрения технических особенностей методы измерения делятся на оптические, пневматические, тензометрические, индуктивные, емкостные, фотоэлектрические и т. д.
В зависимости от того, находится ли средство измерения в контакте с измеряемым объектом, методы измерения делятся на контактные и бесконтактные.
Все методы измерений поддаются систематизации и обобщению по характерным признакам.
Методы измерений подразделяются на:
·
метод непосредственной оценки;
·
методы сравнения с мерой: дифференциальный, противопоставления, нулевой, совпадений, методы измерения замещением и дополнением.
Что такое метод непосредственной оценки?
Метод непосредственной оценки – метод измерений, при котором значение величины определяют непосредственно по показывающему средству измерений.
Метод непосредственной оценки дает значение измеряемой величины непосредственно по отсчетному устройству измерительного прибора прямого действия (измерение размера детали микрометром, давления – деформационным манометром, температуры – термометром, силы электрического тока – амперметром и т.п.). При этом применяют в основном показывающие измерительные приборы.
При методе непосредственной оценки измерение проводится быстро, в один прием, результат получается сразу. Однако точность измерения невысока из-за погрешностей, связанных с необходимостью градуировки шкал приборов и влиянием посторонних величин.
Точность измерения можно повысить, сравнивая измеряемое значение величины непосредственно с мерой.
Что такое методы сравнения с мерой?
Метод сравнения с мерой – метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой мерой.
Например: измерение массы на рычажных весах с уравновешиванием гирями (мерами массы с известным значением), или измерение напряжения постоянного тока на компенсаторе сравнением с известной ЭДС нормального элемента.
Методы сравнения с мерой подразделяются на дифференциальный, нулевой, метод совпадений, измерений замещением и дополнением, метод противопоставления.
В чем состоит дифференциальный метод измерений?
Дифференциальный метод измерений – метод измерений, при котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, при котором измеряется разность между этими двумя величинами. Например, измерения, выполняемые при поверке мер длины сравнением с эталонной мерой на компараторе.
Метод позволяет получать результаты с высокой точностью, однако осуществление метода возможно только при условии воспроизведения с большой точностью известной величины, значение которой близко к значению измеряемой.
Сущность метода рассмотрена на примере измерения размера детали в стойке с измерительной головкой (рисунок 1). Для настройки прибора подбирают блок концевых мер, размер которого L близок к размеру измеряемой детали, и чаще всего равен номинальному.
По блоку мер перемещением кронштейна по стойке создают необходимый натяг и настраивают головку на нуль. Снимают блок концевых мер и по детали определяют отклонение Q. Затем вычисляют действительный размер изделия x = L+Q. Предположив, что допускаемая погрешность измерения не превышает ±D, определяют, что относительная погрешность результата измерения Q равна ± D/Q, а размера детали ± D/(L+Q). Так как L значительно больше Q, то относительная погрешность размера детали х значительно меньше относительной погрешности результата измерения Q, т. е. ± D/(L+Q)< ±D/Q.
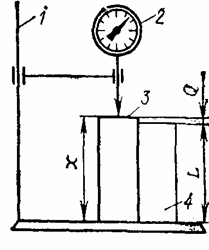
Рисунок 1 – Схема измерения длины дифференциальным методом:
1 – стойка; 2 – измерительная головка; 3 – измеряемая деталь;
4 – блок концевых мер
Пусть L=50 мм; Q = 0,5 мм; D = ±0,005 мм, тогда D/Q = ±0,01(±1%), a D/(L+Q) = ±0,0001 (±0,01%). Таким образом, для достижения такой высокой точности можно воспользоваться сравнительно грубым прибором и весьма точной мерой,
Этим методом, часто используемым в технических измерениях, с помощью измерительных головок, индикаторных и рычажных скоб, оптиметров, индикаторных и микрометрических нутромеров определяют размеры деталей и отклонения. Дифференциальный метод используется в неуравновешенных мостах постоянного тока.
В чем состоит нулевой метод измерений?
Нулевой метод измерений – метод сравнения с мерой, в котором результирующий эффект воздействия измеряемой величины и меры на прибор сравнения доводят до нуля.
Например, измерение электрического сопротивления мостом с полным его уравновешиванием; взвешивание грузов на рычажных весах; измерение сопротивления, емкости и индуктивности при помощи уравновешенных мостов постоянного и переменного тока. В истории развития техники точных измерений нулевой метод появился одним из первых.
Нулевой и дифференциальный методы очень близки. Если в дифференциальном методе измеряют разность между значениями двух величин, то в нулевом практически приводят эту разность к нулю. Часто нулевой метод превращается в дифференциальный. Недостаток нулевого метода заключается в необходимости иметь средство измерений, позволяющее воспроизводить любое значение известной величины без существенного понижения точности. В большинстве случаев для этого используют меры переменного значения или наборы мер.
В чем состоит метод совпадений?
Метод совпадений – метод сравнения с мерой, в котором разность между измеряемым значением величины и значением, воспроизводимым мерой, измеряют, используя совпадения отметок шкал или периодических сигналов известной и неизвестной величин.
Например, нониус для отсчета долей делений основной шкалы; сравнение радиосигналов точного времени с ходом хронометра; измерение частоты вращения вибрационными и стробоскопическими тахометрами; измерение длин интерферометром и т.п.
В чем состоит метод измерений замещением?
Метод измерений замещением – метод сравнения с мерой, в котором измеряемую величину заменяют мерой с известным значением величины.
Например, взвешивание с поочередным помещением измеряемого объекта и гирь на одну и ту же чашку весов (метод Борда). При использовании данного метода при измерении малого напряжения с помощью высокочувствительного гальванометра к прибору сначала подключают источник неизвестного напряжения и определяют отклонение указателя. Затем с помощью регулируемого источника известного напряжения добиваются того же отклонения указателя прибора. В этом случае неизвестное напряжение принимается равным известному.
В чем состоит метод измерений дополнением?
Метод измерений дополнением – метод сравнения с мерой, в котором значение измеряемой величины дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению.
В чем состоит метод противопоставления?
Метод противопоставления – метод, в котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения, с помощью которого устанавливается соотношение между этими величинами.
Например, измерение линейных штриховых мер на компараторе.
Чем различаются контактные и бесконтактные методы измерения?
Контактный метод измерений – метод измерений, основанный на том, что чувствительный элемент прибора приводится в контакт с объектом измерения.
Например: измерение диаметра вала измерительной скобой или контроль проходным и непроходным калибрами; измерение температуры тела термометром.
Бесконтактный метод измерений – метод измерений, основанный на том, что чувствительный элемент средства измерений не приводится в контакт с объектом измерения.
Например: измерение температуры в доменной печи пирометром; измерение расстояния до объекта радиолокатором.
Что такое средство измерений?
Средство измерений – техническое средство, предназначенное для измерений, имеющее нормированные метрологические характеристики, воспроизводящее и (или) хранящее единицу физической величины, размер которой принимают неизменным (в пределах установленной погрешности) в течение известного интервала времени.
Данное определение отражает суть средства измерений заключающуюся, во-первых, в способности хранить (или воспроизводить) единицу физической величины; во-вторых, в неизменности размера хранимой единицы. Эти важнейшие факторы и обусловливают возможность выполнения измерения (сопоставление с единицей измерений), т. е. "делают" техническое средство средством измерений. Если же размер единицы в процессе измерений изменяется более, чем установлено нормами, таким средством измерений нельзя получить результат с требуемой точностью. Это означает, что измерять можно лишь тогда, когда техническое средство, предназначенное для этой цели, может хранить единицу, достаточно неизменную по размеру и во времени.
На какие виды подразделяются средства измерений?
Средства измерений делятся на виды: меры, измерительные приборы, измерительные преобразователи, измерительные установки и системы.
Что такое мера?
Мера физической величины (мера величины) – средство измерений, предназначенное для воспроизведения и (или) хранения физической величины одного или нескольких заданных размеров, значения которых выражены в установленных единицах и известны с необходимой точностью.
Мера представляет собой простейшее средство измерений в виде тела или устройства. Например, гиря, плоскопараллельная концевая мера длины, линейка с делениями, катушка электрического сопротивления, нормальный элемент.
Различают разновидности мер:
- однозначная мера – мера, воспроизводящая физическую величину одного размера. Например, гиря, конденсатор, резистор:
- многозначная мера – мера, воспроизводящая ряд одноименных величин различного размера. Например, линейка с миллиметровыми делениями, конденсатор переменной емкости;
- набор мер – комплект мер разного размера одной и той же физической величины, предназначенных для применения как в отдельности, так и в различных сочетаниях. Например, набор концевых мер длины;
- магазин мер – набор мер, конструктивно объединенный в единое устройство, в котором имеются приспособления для их соединения в различных комбинациях. Например, магазин электрических сопротивлений.
К мерам относятся также калибры, стандартные образцы и образцовые вещества.
Калибры – меры, предназначенные для контроля размеров или формы изделий, или взаимного положения их частей.
Стандартные образцы и образцовые вещества представляют собой меры в виде тела или вещества определенного и строго регламентированного содержания (образцы шероховатости, твердости, чистых металлов и т. д.).
Стандартный образец – это образец вещества (материала) с установленным в результате метрологической аттестации значением одной или более величин, характеризующих свойства или состав этого вещества (материала).
Что такое измерительный прибор?
Измерительный прибор – это средство измерений, предназначенное для выработки сигнала измерительной информации о величине, подлежащей измерению, в форме, доступной для непосредственного восприятия наблюдателем.
Измерительный прибор в отличие от меры не воспроизводит известное значение величины, а она должна подводиться к нему извне, воздействовать на него тем или иным способом. В ряде случаев измеряемая величина подводится к прибору через измерительный преобразователь. В этом случае на прибор воздействует преобразованная величина.
Наиболее распространены приборы прямого действия, в которых сигнал измерительной информации один или несколько раз преобразуется в одном направлении.
Что такое измерительный преобразователь?
Измерительный преобразователь – средство измерений, служащее для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки или хранения, но неподдающейся непосредственному восприятию наблюдателем.
Измерительные преобразователи это конструктивно обособленные элементы, однако самостоятельного значения для проведения измерений не имеют. Они являются составными частями измерительных приборов, систем автоматического контроля, управления и регулирования.
По месту, занимаемому в приборе, преобразователи подразделяются на первичные, промежуточные и передающие,
Преобразуемая физическая величина называется входной, а результат преобразования – выходной величиной. Связь между выходной и входной величинами уста
Что такое измерительная установка и измерительная система?
Измерительная установка – это совокупность функционально объединенных средств измерений (мер, измерительных приборов, измерительных преобразователей) и вспомогательных устройств, предназначенных для выработки сигналов измерительной информации в форме, удобной для непосредственного восприятия наблюдателем, и расположенных в одном месте. Например, весовая, для испытания материалов, диагностическая установки.
Измерительная система отличается от измерительной установки тем, что она предназначена для выработки сигналов измерительной информации в форме, удобной не только для восприятия наблюдателем, но и для автоматической обработки результатов измерений, передачи на расстояние или использования в автоматических системах управления.
Как классифицируются средства измерений?
Средства измерения классифицируются по независимым признакам.
1. По роду измеряемых величин или параметров – на средства измерений для измерения линейных и угловых величин, температуры, давления и разрежения, количества и расхода вещества, массы, влажности, электрических величин, уровня, частоты вращения, сил и моментов и др.
2. По принципу действия – на средства измерений механические, электрические, жидкостные, пневматические, оптические, радиоактивные и др.
3. По метрологическому назначению – на средства измерений эталонные, лабораторные и технические (рабочие).
4. По способу образования показаний – на средства измерений показывающие и регистрирующие.
5. По числу контролируемых величин – на средства измерений одноточечные и многоточечные, а также информационно-измерительные системы для большого числа параметров.
6. По способу определения значения измеряемой величины – на средства измерений прямого действия и сравнения.
7. По дистанционному признаку – на средства измерений местные, с дистанционной передачей показаний и телеметрического контроля.
8. По точности – на средства измерений, имеющие классы точности, обозначаемые цифрами 0,1; 0,15; 0,2; 0,25; 0,4; 0,5; 0,6; 1,0; 1,5; 2,0; 2,5; 4,0.
Измерительные приборы по вышеуказанной классификации могут быть отнесены одновременно к нескольким группам, т.е. манометр может быть механическим, техническим, показывающим, с дистанционной передачей, класса точности 2,5. Поэтому в качестве основной принята классификация, по которой условные наименования приборы получают в зависимости от рода измеряемых величин или параметров.
Классификация приборов по другим признакам является дополнительной и позволяет более полно характеризовать рассматриваемые средства измерений.
Чем отличаются технические, лабораторные и эталонные приборы?
Технические приборы являются рабочими средствами измерений, применяемыми для конкретных измерений в производстве.
Лабораторные приборы служат обычно для точных измерений при исследовательских и наладочных работах, а также при проведении агрохимических анализов.
Эталонные приборы предназначены для поверки технических и лабораторных средств измерений.
Чем отличаются показывающие и регистрирующие приборы?
Показывающие приборы делятся на аналоговые и цифровые.
Аналоговые приборы – стрелочные с отсчетным устройством, состоящим из шкалы и указателя, связанного с подвижной частью прибора. Их показания являются непрерывной функцией значений измеряемой величины.
Цифровые приборы автоматически вырабатывают дискретные сигналы измерительной информации. Их показания представлены в цифровой форме.
Регистрирующие приборы подразделяют на самопишущие и печатающие.
Самопишущие приборы выдают показания в форме диаграммы.
Печатающие приборы представляют результат в цифровой форме на бумажной ленте.
Чем отличаются приборы прямого действия и приборы сравнения?
Приборы прямого действия (непосредственной оценки) позволяют получать значения измеряемой величины на отсчетном устройстве (показывающие манометры, термометры, тахометры, динамометры и т. д.). Они состоят из нескольких элементов, преобразующих сигнал измерительной информации в одном направлении.
Приборы сравнения дают возможность определять значение измеряемой величины сравнением с известным значением, воспроизводимым мерой. Эти значения сравниваются нулевым или дифференциальным методами при помощи компенсационных или мостовых измерительных цепей. Компенсационные цепи применяют для сравнения активных величин, мостовые – пассивных. Погрешности измерения приборов сравнения определяются в основном погрешностью мер. Эти приборы более точные, чем приборы прямого действия.
В чем отличия приборов по дистанционному признаку?
Местные приборы устанавливают непосредственно в местах измерений или технологического контроля.
Приборы с дистанционной передачей показаний (до 300 м) монтируют на щиты управления.
Средства телеметрических измерений позволяют измерять различные величины на значительном удалении прибора от объекта.
Что такое автоматическое средство измерений?
Автоматическое средство измерений – средство измерений, производящее без непосредственного участия человека измерения и все операции, связанные с обработкой результатов измерений, их регистрацией, передачей данных или выработкой управляющего сигнала.
Автоматическое средство измерений, встроенное в автоматическую технологическую линию, нередко называют "измерительный автомат" или "контрольный автомат". В гибких производственных системах (ГПС) применяются "измерительные роботы", под которыми нередко понимается "разновидность контрольно-измерительных машин, отличающаяся хорошими манипуляционными свойствами, высокими скоростями перемещений и измерений".
Что такое автоматизированное средство измерений?
Автоматизированное средство измерений – средство измерений, производящее в автоматическом режиме одну или несколько измерительных операций.
Например, барограф (измерение и регистрация результатов). Электрический счетчик электроэнергии (измерение и регистрация данных нарастающим итогом).
Какова общая структура измерительных приборов?
Измерительный прибор состоит из совокупности измерительных преобразователей и отсчетного устройства и обладает заданными метрологическими свойствами. Независимо от конкретного физического и конструктивного исполнения средства измерений могут быть представлены структурными схемами, показывающими состав прибора или системы и связи между отдельными их частями, выполняющими те или иные функции.
В измерительных приборах числовые значения измеряемой величины получатся после того, как она тем или иным способом преобразована. Исключений очень мало (при помощи штангенциркуля длина измеряется без преобразований, а в микрометре для отсчета долей миллиметра их преобразуют с помощью микрометрической пары в перемещение указателя по окружности).
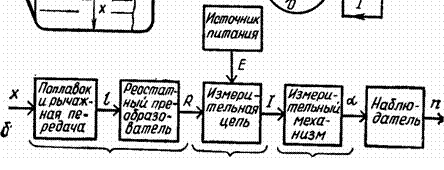
Структурная схема измерительного прибора рассмотрена на рисунке 2, где показано устройство электромеханического прибора для измерения уровня топлива в баке автомобиля. Высота измеряемого уровня х воспринимается поплавком 1, который с помощью рычажной передачи 2 перемещает движок реостата R.
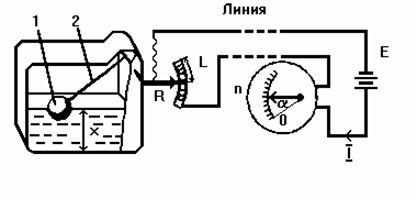
Рисунок 2 - Функциональная схема топливного уровнемера:
Измерительный Измерительное Указатель
преобразователь устройство
Рисунок 3 - Структурная схема топливного уровнемера
Эта часть устройства обеспечивает однозначную функциональную зависимость перемещения l от измеряемой величины х. Реостат с равномерной намоткой дает однозначную зависимость R=f(l). Электрическая измерительная цепь (при постоянстве напряжения Е источника питания и всех сопротивлений цепи, кроме сопротивления реостата) осуществляет однозначную зависимость тока I от сопротивления R. Поэтому шкала электроизмерительного прибора (указателя), по которой отсчитываются показания n, может быть проградуирована непосредственно в значениях измеряемого уровня жидкости.
Все измерительные преобразования, используемые в топливном уровнемере (рисунок 2), можно изобразить последовательной цепью x®l®R®I®a®n, или представить структурной схемой цепи (рисунок 3). Здесь преобразование a®n – отсчет и регистрация показаний, проводимые при использовании визуального указателя человеком-наблюдателем, а в регистрирующих приборах - осуществляемые автоматически без участия человека.
Как разделяются измерительные преобразователи?
С метрологической позиции методы измерительных преобразований можно разделить на два основных класса, принципиально отличающихся друг от друга: метод прямого преобразования и метод уравновешивания.
Метод прямого преобразования, структурная схема которого рассмотрена на примере электромеханического уровнемера топлива (рисунок 2), характеризуется тем, что все измерительные преобразования проходят только в одном прямом направлении – от входной величины через цепь преобразований к выходной величине на указатель.
Структурная схема приборов прямого преобразования разомкнутая, а результирующая чувствительность определяется произведением чувствительностей всех составляющих его преобразователей.
Метод уравновешивания определяется использованием двух цепей преобразований, функции которых различны (рисунок 4).
Измеряемая величина х преобразуется по цепи К, прямого преобразования, состоящей из преобразователей К1К2, усиливается и поступает на выход. В приборе существует также цепь обратного уравновешивания
![]() , которая создает величину xy , однородную с входной, и уравновешивает ее. В результате этого на вход цепи К, поступает только небольшая часть входной преобразуемой величины х, равная разности х—xy, и цепь К служит лишь для обнаружения степени неравновесия.
, которая создает величину xy , однородную с входной, и уравновешивает ее. В результате этого на вход цепи К, поступает только небольшая часть входной преобразуемой величины х, равная разности х—xy, и цепь К служит лишь для обнаружения степени неравновесия.
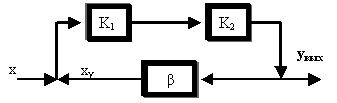
Рисунок 4 - Структурная схема метода уравновешивания
Метод уравновешивания реализован в приборах сравнения. Структурная схема таких приборов замкнутая.
Измерительные приборы в общем случае включают в себя три самостоятельных конструктивных элемента: измерительный преобразователь (датчик), измерительное устройство и указатель (или регистратор), которые размещаются совместно или раздельно и соединяются между собой кабелем или другой линией связи.
Что такое метрологическая характеристика средства измерений?
Метрологическая характеристика средства измерений – характеристика одного из свойств средства измерений, влияющая на результат измерений и на его погрешность. Для каждого типа средства измерений устанавливают свои комплексы метрологических характеристик.
Что такое нормируемые метрологические характеристики
типа средств измерений
Нормируемые метрологические характеристики типа средств измерений – совокупность метрологических характеристик данного типа средств измерений, устанавливаемая нормативно-техническими документами на средства измерений.
Каковы основные метрологические характеристики
средств измерений?
Метрологические характеристики определяют эксплуатационные свойства средства измерений, и указываются в прилагаемой к нему технической документации. Их можно разделить на группы:
1 Характеристики, предназначенные для определения показаний СИ: функция преобразования измерительного преобразователя; значения однозначной или многозначной меры; цена деления шкалы измерительного преобразователя или многозначной меры; вид выходного кода, число разрядов кода, цена единицы наименьшего разряда кода СИ, предназначенного для выдачи ре-зультатов в цифровом коде.
2 Характеристики качества показаний – точности и правильности. Точность показаний определяется средним квадратическим отклонением. Правильность обеспечивается внесением поправки, устанавливаемой при поверке, калибровке или метрологической аттестации СИ.
3 Характеристики чувствительности СИ к влияющим величинам: функции влияния, учет изменений метрологических характеристик СИ, вызванных изменениями влияющих величин в установленных пределах.
4 Динамические характеристики СИ, учитывающие их инерционные свойства.
5 Характеристики взаимодействия с объектами или устройствами на входе и выходе СИ, например, входной и выходной импедансы линейного измерительного преобразователя.
6 Неинформативные параметры выходного сигнала, обеспечивающие нормальную работу устройств, подключенных к СИ. Например, выходным сигналом преобразователя напряжения в среднюю частоту следования импульсов является последовательность импульсов. Частотомер, подключаемый к выходу преобразователя, будет работать при определенных амплитуде и форме импульсов преобразователя, которые и являются неинформативными параметрами.
Для определения метрологических характеристик средство измерений должно пройти испытания типа, а затем поверку.
Каковы метрологические характеристики
для определения показаний средства измерений?
Основные характеристики шкалы отсчетного устройства прибора следующие.
Длина (интервал) деления шкалы – расстояние между осями или центрами двух соседних отметок шкалы, измеренное вдоль линии, проходящей через середины ее самых коротких отметок.
Цена деления – разность значений измеряемой величины, соответствую-щих двум соседним отметкам шкалы.
Диапазон показаний измерительного прибора со шкальным отсчетным устройством – это область значений шкалы прибора, ограниченная начальным и конечным значениями шкалы.
Диапазон измерений – это область значений величины, в пределах которой нормированы допускаемые пределы погрешности средства измерений. Он ограничивается верхними и нижними пределами измерений.
По диапазонам показаний и измерений устанавливают область применения измерительных приборов.
Что такое вариация показаний СИ?
Вариация показаний – разность показаний СИ в одной и той же точке диапазона измерений при плавном переходе к этой точке со стороны меньших и больших значений измеряемой величины. При нескольких медленных подходах к данной точке диапазона измерения в каждом из двух направлений вариация b определяется как абсолютное значение средней разности показаний
![]() и
и
![]() :
:
![]() . (7)
. (7)
Причинами вариации являются трение и мертвый ход подвижных частей, наличие зазоров в сочленениях механизмов приборов, старение материалов, механический и магнитный гистерезис элееличи.
Что такое погрешность средств измерений?
Главной метрологической характеристикой измерительных средств еличяется их погрешность. В результате воздействия большого числа случайных и детерминированных факторов, возникающих в процессе изготовления, хранения и эксплуатации показания средств измерений отличаются от истинных значений измеряемых ими величин. Эти отклонения определяют погрешности СИ.
Погрешность средств измерений – это разность между показанием средства измерений и истинным (действительным) значением измеряемой физической величины.
Поскольку истинное значение физической величины неизвестно, то на практике пользуются ее действительным значением.
Погрешность результата измерений определяет качество измерений и в значительной мере зависит от погрешности средств измерений.
Как классифицируются погрешности средств измерений?
Погрешности средств измерений классифицируются по признакам:
·
по отношению к условиям применения – основные и дополнительные;
·
по способу выражения – абсолютные, относительные и приведенные;
·
по характеру проявления возможностей устранения и причинам возникновения – систематические и случайные;
·
по отношению к измеряемой величине – динамические и статические;
·
по способу суммирования – аддитивные и мультипликативные.
Что такое основная и дополнительная погрешности СИ?
Основная погрешность средств измерений – это погрешность средств измерений, определяемая в нормальных условиях его применения:
![]() или
или
![]() , где
, где
![]() и
и
![]() выражаются в единицах измеряемой величины.
выражаются в единицах измеряемой величины.
Дополнительная погрешность средств измерений – это составляющая погрешности средства измерений, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от ее нормального значения или ее выхода за пределы нормальной области значений.
Нормальные условия регламентируются соответствующими техническими условиями и стандартами на средства измерения конкретного типа. Дополнительные погрешности, появляющиеся при отклонении условий эксплуатации средств измерений от нормальных, могут нормироваться раздельно для каждого из влияющих факторов.
Что такое абсолютная, относительная и приведенная
погрешности СИ?
Абсолютная погрешность средств измерений – это разность между показанием прибора и истинным (действительным) значением измеряемой еличиины. Действительное значение величины устанавливают, используя эталонное средство измерений.
Абсолютная погрешность оценивает точность прибора только в одной точке диапазона измерений и выражается в единицах измеряемой величины:
![]() , (8)
, (8)
где
![]() – показания прибора;
– показания прибора;
![]() – действительное значение измеряемой величины.
– действительное значение измеряемой величины.
Относительная погрешность средств измерений – погрешность средств измерений, выраженная отношением абсолютной погрешности к действительному значению физической величины, в пределах диапазона измерений. Относительная погрешность средства измерения (%) определяется как
![]() , (9)
, (9)
где
![]() – абсолютная погрешность;
– абсолютная погрешность;
![]() – показания прибора.
– показания прибора.
Относительная погрешность оценивает точность прибора также в одной точке и переменна по диапазону измерений.
Если диапазон измерения прибора охватывает и нулевое значение величины, то относительная погрешность обращается в бесконечность в соответствующей ему точке шкалы.
Приведенная погрешность средств измерений – относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона. Условно принятое значение величины называют нормирующим значением. Приведенную погрешность обычно выражают в процентах и определяют по формуле
![]() , (10)
, (10)
где
![]() – нормирующие значения.
– нормирующие значения.
Приведенная погрешность характеризует постоянную точность измерительного прибора по всему диапазону измерений.
Например, значения абсолютной, относительной, приведенной погрешности потенциометра с верхним пределом измерений 150 °С при
![]() =120°С, листвительным значением измеряемой температуры
=120°С, листвительным значением измеряемой температуры
![]() =120,6 °С и нормирующим значением верхнего предела измерений
=120,6 °С и нормирующим значением верхнего предела измерений
![]() = 150°С будут, соответствен-но, составлять
= 150°С будут, соответствен-но, составлять
![]() = –0,6°С, d = –0,5%, g = –0,4%.
= –0,6°С, d = –0,5%, g = –0,4%.
Если границы погрешностей средств измерений необходимо принять изменяющимися нелинейно, пределы допускаемых погрешностей устанавливают в виде графика, таблицы или по другим формулам.
Как устанавливается нормирующее значение?
Нормирующее значение при установлении приведенной погрешности принимается равным:
·
для средств измерений с равномерной или степенной шкалой
- конечному значению рабочей части шкалы, если нулевая отметка находится в начале шкалы;
- арифметической сумме конечных значений рабочей части шкалы без учета их знака, если нулевая отметка находится внутри рабочей части шкалы;
·
для мер – их номинальному значению;
·
для средств измерений с логарифмической или гиперболической шкалой
- длине шкалы.
Что такое статическая и динамическая погрешности СИ?
Статическая погрешность средства измерений – это погрешность средства измерений, применяемого при измерели физической величины, принимаемой за неизменную.
Динамическая погрешность средства измерений – это погрешность средства измерений, возникающая при измерении изменяющейся (в процессе измерений) физической величины.
Что такое предел допускаемой погрешности
Предел допускаемой погрешности средств измерений – наибольшее значение погрешности средства измерений, при котором оно может быть признано годным и допущено к применению. В случае превышения установленного предела средство измерений остается непригодным к применению.
Например, предел допускаемой приведенной погрешности амперметра класса 1,0 равен ±1% от верхнего предела измерений, т. Е. при верхнем пределе измерений 10 А предел допускаемой приведенной погрешности составит 0,1%.
Что такое систематическая погрешность?
Систематической погрешностью средства измерений
![]() называют составляющую погрешности измерений, принимаемую за постоянную или закономерно изменяющуюся. Систематические погрешности возникают из-за неисправности средства измерений, неправильной его установки, настройки, лияяяния неблагоприятных внешних условий (вибрации, температуры и влажности воздуха, отклонения напряжения и т. П.), износа. Они зависят также от индивидуальных особенностей оператора.
называют составляющую погрешности измерений, принимаемую за постоянную или закономерно изменяющуюся. Систематические погрешности возникают из-за неисправности средства измерений, неправильной его установки, настройки, лияяяния неблагоприятных внешних условий (вибрации, температуры и влажности воздуха, отклонения напряжения и т. П.), износа. Они зависят также от индивидуальных особенностей оператора.
![]() в точке х диапазона измерений оценивают по формуле:
в точке х диапазона измерений оценивают по формуле:
![]() , (11)
, (11)
где
![]() и
и
![]() — среднее значение погрешности в точке диапазона измерений, определяемое экспериментально при медленных многократных измерениях информативного параметра входного или выходного сигнала со стороны соответственно меньших и больших значений х.
— среднее значение погрешности в точке диапазона измерений, определяемое экспериментально при медленных многократных измерениях информативного параметра входного или выходного сигнала со стороны соответственно меньших и больших значений х.
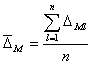 ;
;
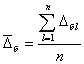
![]() , (12)
, (12)
где
![]() и
и
![]() — l-я реализация (отсчет) погрешности средства измерений при предварительном изменении информативного параметра входного или выходного сигнала со стороны меньших и больших значений до значения х соответственно; п — число опытов при определении
— l-я реализация (отсчет) погрешности средства измерений при предварительном изменении информативного параметра входного или выходного сигнала со стороны меньших и больших значений до значения х соответственно; п — число опытов при определении
![]() и
и
![]() . Если вариация не учитывается или отсутствует, то
. Если вариация не учитывается или отсутствует, то
![]() определяют по формуле:
определяют по формуле:
![]() , (13)
, (13)
где
![]() – i-й отсчет погрешности средства измерений.
– i-й отсчет погрешности средства измерений.
Нормируется систематическая составляющая
![]() погрешности пределом допускаемой составляющей
погрешности пределом допускаемой составляющей
![]() погрешности.
погрешности.
Систематическая погрешность одного средства измерений, как правило, будет отличаться от систематической погрешности другого экземпляра средства измерений этого же типа, вследствие чего для группы однотипных средств измерений систематическая погрешность может иногда рассматриваться как случайная погрешность.
Что такое случайная погрешность средства измерений?
Случайной
![]() называют составляющую погрешности измерений, изменяющуюся случайным образом при повторных измерениях одной и той же величины.
называют составляющую погрешности измерений, изменяющуюся случайным образом при повторных измерениях одной и той же величины.
Случайная погрешность возникает при одновременном воздействии многих независимых факторов, каждый из которых несущественно влияет на результат измерений, а суммарное воздействие может быть значительным.
Случайную погрешность
![]() оценивают средним квадратическим отклонением S(
оценивают средним квадратическим отклонением S(
![]() ) по формуле:
) по формуле:
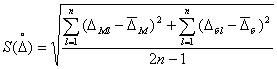 . (14)
. (14)
Если вариация не учитывается или отсутствует, то
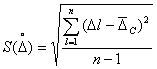 . (15)
. (15)
Нормируется случайная составляющая погрешности пределом допускаемого среднего квадратического отклонения случайной составляющей погрешности средства измерения SД(
![]() ).
).
Что такое аддитивная и мультипликативная погрешности?
В зависимости от влияния на результат измерений погрешности измерений можно разделить на аддитивные и мультипликативные.
Аддитивная погрешность проявляется в результате измерений посредством сложения с измеряемой величиной. Например, систематическими аддитивными погрешностями являются погрешности от постороннего груза на чашке весов, от неточной установки прибора на нуль перед измерением, от термо-э.д.с. в цепях переменного тока; случайные аддитивные погрешности могут возникать от наводки переменной э.д.с. на вход прибора, от тепловых шумов, от трения в опорах подвижной части измерительного механизма, от ненадежного контакта при измерении сопротивления, от порога трогания приборов с ручным или автоматическим уравновешиванием.
Мультипликативная погрешность проявляется в результате измерений посредством перемножения с измеряемой величиной. Например, погрешности от изменения коэффициента усиления усилителя, изменения жесткости мембраны датчика манометра или пружины прибора, изменения опорного напряжения в цифровом вольтметре, от изменения чувствительности преобразователя.
Что такое точность средств измерений?
Точность средства измерений – характеристика качества средства измерений, отражающая близость его погрешности к нулю.
Что такое класс точности средства измерений?
Учет всех нормируемых метрологических характеристик средств измерений – сложная и трудоемкая процедура, проводимая только при измерениях очень высокой точности, характерных для метрологической практики. В обиходе и на производстве такая точность не рациональна. Поэтому для средств измерений, используемых в повседневной практике, принято деление по точности на классы.
Класс точности средств измерений – это обобщенная характеристика данного типа средств измерений, как правило, отражающая уровень их точности, выражаемая пределами допускаемых основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность.
Например, класс точности концевых мер длины характеризует близость их размера к номинальному, допускаемое отклонение от плоскопараллельности, а также притираемость и стабильность; класс точности вольтметров характеризует пределы допускаемой основной погрешности и допускаемых изменений показаний, вызываемых внешним магнитным полем и отклонением от нормальных значений температуры, частоты переменного тока и некоторых других величин.
Класс точности дает возможность судить о том, в каких пределах находится погрешность средств измерений одного типа, но не является непосредственным показателем точности измерений, выполняемых с помощью каждого из этих средств. Они удобны для сравнительной оценки качества СИ, их выбора, международной торговли. Но по ним трудно установить градацию СИ по точности, у которых нормируется комплекс метрологических характеристик. Устанавливаются по ГОСТ 8.401 – 80 «ГСИ. Классы точности средств измерений. Общие положения».
Классы точности конкретных типов СИ устанавливаются стандартами, содержащими технические требования к средствам измерений.
СИ с двумя или более диапазонами измерений одной и той же физической величины допускается присваивать два или более класса точности. СИ, предназначенным для измерения двух или более физических величин, допускается присваивать различные классы точности для каждой измеряемой величины (например, цифровой вольтметр – омметр имеет два класса точности).
С целью ограничения номенклатуры СИ по точности для СИ конкретного типа устанавливают ограниченное число классов точности.
Классы точности цифровых измерительных приборов со встроенными вычислительными устройствами для обработки результатов измерений устанавливают без учета режима обработки.
Присваивается класс по результатам приемочных испытаний и может понижаться по результатам поверки.
Основой для присвоения измерительным приборам того или иного класса точности является допускаемая основная погрешность и способ ее выражения. Пределы допускаемой основной погрешности выражают в форме приведенной, относительной или абсолютной погрешностей. Форма зависит от характера изменения погрешностей в пределах диапазона измерений, а также от условий применения и назначения средств измерений конкретного вида.
Метрологические характеристики, определяемые классом точности, нормируются следующим образом:
Ø
в форме приведенных погрешностей – если границы погрешностей можно получить практически неизменными в пределах диапазона измерений;
Ø
в форме относительных погрешностей – если указанные границы нельзя полагать постоянными;
Ø
в форме абсолютных погрешностей (т.е. в единицах измеряемой величины или в делениях шкалы СИ) – если погрешность результатов измерений в данной области измерений принято выражать в единицах измеряемой величины или в делениях шкалы. Например, для мер массы или длины.
Если границы абсолютных погрешностей можно полагать практически неизменными, то пределы допускаемых погрешностей имеют вид:
Dn = ±а. (16)
Если границы относительных погрешностей можно полагать практически неизменными:
dn =
![]() = q. (17)
= q. (17)
Если границы абсолютных погрешностей можно полагать изменяющимися практически линейно:
Dn = ±(a + вхn), (18)
Тогда для относительных погрешностей:
![]() или
или
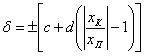 , (19)
, (19)
где Dn – пределы допускаемой абсолютной основной погрешности выраженной в единицах измеряемой величины на входе (выходе) или условно в делениях шкалы; хn – значение измеряемой величины на входе (выходе) СИ или число делений, отсчитываемых по шкале; а, в – положительные числа, не зависящие от хn; dn – пределы допускаемой относительной основной погрешности, %;
q – отвлечённое число, выбираемое из ряда; Хк – больший (по модулю) из пределов измерений; c, d – положительные числа, c = в + d; d =
![]() /
/
Указание только абсолютной погрешности не позволяет сравнивать между собой по точности приборы с разными диапазонами измерений. Поэтому для электрических измеряемых приборов, манометров, приборов измерения изиико-химических величин и др. устанавливаются пределы допускаемой приведённой погрешности:
g =
![]() = ±р, %, (20)
= ±р, %, (20)
где XN – нормирующее значение, выраженное в единицах Dn; р – отвлечённое положительное число, выбираемое из выше приведенного ряда.
Рассчитанные значения q, c, d или p округляются до ближайшего большего значения по ряду:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() (где n = 1; 0; –1; –2 и т.д.).
(где n = 1; 0; –1; –2 и т.д.).
Нормирующее значение XN выбирают в зависимости от вида и характера шкалы прибора. Если прибор имеет равномерную шкалу и нулевая отметка находится на краю шкалы или вне её, то за XN принимают конечное значение шкалы. Для таких же приборов, но с нулевой отметкой внутри шкалы, XN равно сумме конечных значений рабочей части шкалы (без учёта знаков). Когда прибор предназначен для измерения отклонения измеряемой величины от номинального значения, за нормирующее значение шкалы принимают это номинальное значение. Если шкала нелинейна (гиперболическая, логарифмическая), то XN равно длине шкалы. Для СИ физической величины, для которых принята шкала с условным нулём, XN устанавливают равным модулю разности пределов измерений. Например для милливольтметра термоэлектрического термометра с пределами 200 и 600°С XN = 400°С. Для частотомеров с диапазоном измерений 45 – 55 Гц и номинальной частотой 50Гц XN = 50Гц.
Пределы допускаемых погрешностей должны быть выражены не более чем двумя значащими цифрами, причем погрешность округления при вычислении пределов должна быть менее 5%.
Как обозначаются классы точности средств измерений?
Для СИ пределы допускаемой основной погрешности, которые выражают в форме приведенной или относительной погрешности (q, p), классы точности обозначают числами, равными этим пределам в %.
![]() Чтобы отличить относительную погрешность от приведенной, на СИ ее обводят 1,5 , т. е. dn = ±1,5%.
Чтобы отличить относительную погрешность от приведенной, на СИ ее обводят 1,5 , т. е. dn = ±1,5%.
Под обозначением класса точности по приведенной погрешности ставят
![]() , т.е. g = ± 0,5%, и записывают без знака
, т.е. g = ± 0,5%, и записывают без знака
![]() , если ХN выражено в единицах величины.
, если ХN выражено в единицах величины.
Если класс точности определяется по относительной погрешности (c, d), то они разделяются чертой «/»:
d = [0,02 + 0,01(
![]() )] %,
)] %,
то класс точности 0,02/0,01.
Класс точности по абсолютной погрешности обозначается римскими цифрами или латинскими буквами в зависимости от пределов значений погрешности.
Обозначение класса точности на средствах измерений дает непосредственное указание на предел допускаемой погрешности. Так, при измерении манометрическим термометром со шкалой 0...150 °С (ХN = 150°С) класса точности 2,5 основная абсолютная погрешность на любой отметке шкалы термометра не превышает по модулю:
![]() .
.
Правила построения и примеры обозначения классов точности приведены в таблице 2.
Таблица 2 – Правила построения и примеры обозначения классов точности
в документации и на средствах измерений
|
Формула для опре-деления пределов допускаемой погрешности |
Примеры пределов в допускаемой основной погрешности |
Обозначение класса точности |
Примечание |
|
|
|
|
в документах |
на средствах измерений |
|
|
|
— |
Класс точности М |
М |
— |
|
|
— |
Класс точности С |
С |
— |
|
|
g=±1,5 |
Класс точности 1,5 |
1,5 |
Если хN выражен в единицах величины |
|
|
g=±0,5 |
Класс точности 0,5 |
0,5 |
Если хN определяет-ся длиной шкалы (ее части) |
|
|
d ±0,5 |
Класс точности 0,5 |
|
— |
|
d=±
|
d=±[0,02+0,01
|
Класс точности 0,02/0,01 |
0,02/0,01 |
— |
Рисунок 5 – Внешний вид приборов
Для средств измерений длин и углов, мер масс и т. п. пределы допускаемой основной погрешности которых принято выражать в форме абсолютных погрешностей (или относительных погрешностей. установленных в виде таблицы, графика), классы точности обозначают, прописными буквами латинского алфавита или римскими цифрами. Классы точности, которым соответствуют меньшие пределы допускаемых погрешностей, изображают буквами, находящимися ближе к началу алфавита, или цифрами, обозначающими меньшие числа (плоскопараллельные концевые меры длины выпускаются классов точности 0, 1, 2, 3). Высший класс точности – 0, низший –3).
Что понимают под терминами «нормальные условия применения средств измерений» и «номинальное значение влияющей величины»?
Нормальные условия применения средств измерений – условия применения средств измерений, при которых влияющие величины имеют номинальные значения или находятся в пределах номинальной области значений. При нормальных условиях определяется основная погрешность средств измерений. Нормальные условия устанавливаются нормативно-техническими документами на средства измерений. Например, нормальное значение температуры для всех видов измерений составляет 20°С (293 К), давление воздуха 100 МПа (750 мм рт. ст.), относительная влажность воздуха 58% и др.
Номинальное значение влияющей величины – значение влияющей величины, устанавливаемое в стандартах на средства измерений данного вида в качестве нормального для этих средств измерений.
Таблица 3 – Номинальные значения влияющих физических величин
|
Влияющая величина |
Номинальное значение влияющей величины |
|
1. Температура для всех видов измерений |
20°С (293 К) |
|
2. Давление окружающего воздуха для измерения иони-зирующих излучений, теплофизических, температурных, маг-нитных, электрических измерений, измерения давления и параметров движения |
100 кПа (750 мм рт. ст.) |
|
3. Давление воздуха для линейных, угловых измерений, измерений массы; силы света, измерений в спектроскопии и других областях, кроме указанных в п. 2 таблицы |
101,3 кПа (760 мм рт. ст.) |
|
4. Относительная влажность воздуха для линейных, угловых измерении, измерений массы, измерений в спектроскопии |
58% |
|
5. Относительная влажность воздуха для измерения элект-рического сопротивления |
55% |
|
6. Относительная влажность воздуха для измерения темпе-ратуры, силы, твердости, переменного электрического тока, ионизирующих излучений, параметров движения |
65% |
|
7. Относительная влажность воздуха для всех видов измерений, кроме указанных в п.п. 4, 5, 6 |
60% |
|
8. Плотность воздуха |
1,2 кг/м3 |
|
9. Ускорение свободного падения |
9,8 м/с2 |
|
10. Магнитная индукция (напряженность магнитного поля) и напряженность электростатического поля для измерений параметров движения, магнитных и электрических величин |
0 |
|
11. Магнитная индукция (напряженность магнитного поля) и напряженность электростатического поля для всех видов измерений, кроме указанных в п. 10 |
Соответствует характеристикам поля Земли в данном географическом районе |
Какие бывают эталоны?
Эталон – это средство измерений (или комплекс средств измерений), предназначенное для воспроизведения и (или) хранения единицы и передачи ее размера нижестоящим по поверочной схеме СИ, утвержденное в качестве эталона в установленном порядке.
Государственный эталон воспроизводит единицу с наивысшей в стране точностью. Эталон-копию применяют вместо государственного эталона для хранения единицы и передачи ее размера рабочим эталонам. Он не всегда является физической копией, но является копией в метрологическом смысле. Эталон сравнения применяют для сличения эталонов, которые не могут быть непосредственно сличаемы друг с другом (например, находятся в различных органах метрологической службы и их нельзя транспортировать).
Рабочий эталон – это эталон, предназначенный для передачи размера единицы рабочим средствам измерений.
Соподчинение эталонов, а также рабочих средств измерений основано на их точности и представлено на схеме (рисунок 6).
Что такое поверка?
Поверка средств измерений – важнейшая форма государственного надзора за средствами измерений. Под поверкой понимают экспериментальное определение погрешности средств измерения и установление их пригодности к применению. Поверку проводят, сличая показания поверяемых средств измерений с эталонами в соответствии с требованиями государственных стандартов на методы и средства поверки, а при их отсутствии – методических указаний (или инструкций) по поверке. Погрешность эталонов должна быть не менее чем в 3 раза меньше ожидаемой погрешности поверяемых средств измерений.
Поверка средств измерения после изготовления или ремонта называется первичной, а проводимая при эксплуатации или хранении средств измерения через определенные промежутки времени (межповерочные интервалы) – периодической. Периодичность поверки средств измерения устанавливают органы государственной метрологической службы, проводящие поверку (1 раз в год или в два года). В случае отказа средств измерений их направляют в ремонт и на следующую поверку независимо от установленного межповерочного интервала.
На средства измерений, признанные в результате поверки годными, наносят поверительные клейма и (или) выписывают свидетельства о поверке; их корпуса пломбируют.
Специально назначенные лица, на которых возложена ответственность за состояние средств измерений, ежегодно составляют календарные графики поверки в виде перечня средств измерений с указанием ее периодичности и календарных сроков. Они должны своевременно представлять средства измерений в ремонт и на поверку в соответствии с графиком, согласованным с территориальной метрологической службой, проводящей поверку, вести учет средств измерений и следить за их состоянием и правильным использованием, определять потребности и составлять заявки на средства измерения и лабораторное оборудование, а также оказывать содействие органам Госстандарта при осуществлении государственного надзора за состоянием и применением средств измерений.
Что такое калибровка средств измерений
и чем она отличается от поверки?
Калибровка – совокупность операций, устанавливающих соотношение между значением величины, полученным с помощью данного средства измерений и соответствующим значением величины, определенным с помощью эталона с целью определения действительных метрологических характеристик этого средства измерений.
Калибровка отличается от поверки такими признаками:
- поверка является контролем метрологических характеристик средств измерений и отвечает на вопрос «годен – не годен» к применению. При калибровке определяются действительные значения метрологических характеристик средств измерений;
- поверка применяется в области распространения государственного метрологического контроля и надзора. Калибровка вне этой области;
- поверку осуществляют органы государственной метрологической службы. Калибровку может осуществлять любая метрологическая служба или физическое лицо, у которых есть для этого условия;
- поверка является обязательной операцией. Калибровка является добровольной операцией.
Какими методами может проводиться поверка (калибровка)?
Метод непосредственного сличения поверяемого (калибруемого) СИ с эталоном соответствующего разряда без использования компаратора (прибора сравнения). Применяются для средств измерений электрических и магнитных величин. Метод основан на проведении одновременных измерений одного и того же значения физической величины однородными (по измеряемой величине) поверяемым (калибруемым) и эталонным средствами измерений. Абсолютная погрешность
D = Хn – Хэ. (21)
Метод может быть реализован двумя способами:
а) регистрацией совмещений, когда указатель поверяемого (калибруемого) прибора изменением входного сигнала совмещают с поверяемой отметкой шкалы, а показания определяют как разность между показанием поверяемого прибора и действительным значением, определяемым по показаниям эталонного прибора;
б) отсчитыванием показаний по шкале поверяемого прибора. Номинальное для поверяемой отметки шкалы значение размера физической величины устанавливают по эталонному СИ, а показания определяют по расстоянию между поверяемой отметкой поверяемого прибора и его указателем.
Первый способ точно определяет погрешность по эталонному прибору, шкала которого обычно имеет большое число делений, а ОУ практически исключает появление погрешности отсчета вследствие параллакса. 2-й способ удобен при автоматической поверке, так как позволяет поверять одновременно несколько средств измерений с помощью одного эталонна. Недостатки метода:
·
нелинейность шкал аналоговых поверяемых приборов;
·
неточность нанесения промежуточных делений, за исключением цифровых СИ.
Достоинства метода:
·
простота;
·
наглядность;
·
возможность автоматической поверки;
·
отсутствие необходимости применения сложного оборудования.
Метод сличения поверяемого (калибруемого) средства измерений с однородным эталонным с помощью компаратора. Иногда невозможно сравнить показания СИ одной и той же величины. Например, нельзя сравнить показания вольтметров, если один из них для измерений только в цепях постоянного тока, а другой переменного; нельзя непосредственно сравнить размеры мер магнитных и электрических величин. Поэтому для их сравнения в схему поверки вводят промежуточное звено – компаратор, который позволяет косвенно сравнивать две однородные или разнородные физические величины (в данном случае компаратором является потенциометр). Компаратором может быть любое СИ, одинаково реагирующие на сигнал, как эталонов, так и поверяемого измерительного прибора.
При сличении мер сопротивления, индуктивности, емкости в качестве компараторов используют мосты постоянного или переменного тока, при сличении мер сопротивления и ЭДС – потенциометры, при сличении мер массы поверяемой (калибруемой) гири с эталонной – весы.
Сличение мер с помощью компараторов осуществляют методами Атиивопоставления или замещения. Общим для этих методов поверки является выработка сигнала о наличии разности размеров сравниваемых величин. Различают также нулевой метод (если сигнал путем подбора эталонной меры или путем принудительного измерения ее размера будет сведен к 0) и дифференциальный метод (при одновременном воздействии сигналов сличаемых мер на входе компаратора измерительный сигнал указывает на наличие разности сравниваемых размеров мер). Метод противопоставления позволяет уменьшить воздействие на результаты поверки влияющих величин, так как они почти одинаково искажают сигналы, подаваемые на вход компаратора. Достоинство метода замещения заключается в последовательном во времени сравнении двух величин.
Метод прямых измерений применяется, когда имеется возможность с помощью многозначной эталонной меры, воспроизводящей в некотором диапазоне, значения величины, в единицах которой отградуировано поверяемое (Алибруемое) СИ, произвести сличение и определить погрешность испытываемого СИ в пределах измерений. Часто применяется при поверке (калибровке) мер электрических и магнитных величин. Например, с помощью калибраторов постоянного электрического напряжения поверяются (калибруются) вольтметры постоянного тока. При выставлении некоторого калиброванного значения напряжения UЭ, подаваемого на поверяемый (калибруемый) прибор, определяется показание последнего UП и П. D = UП - UЭ. Этот метод аналогичен методу непосредственного сличения для однозначных мер.
Метод косвенных измерений величины, позволяющий действительный размер меры находить с помощью поверяемого (калибратора) СИ прямыми измерениями нескольких эталонных величин, связанных с искомой величиной, определяются зависимостью. Применяется, когда действительные значения величин, воспроизводимые эталонным и измеряемые поверяемым СИ, невозможно определить прямыми измерениями или когда косвенные измерения более просты или точны по сравнению с прямыми.
Систематическую составляющую относительной погрешности электрического счетчика активной электрической энергии находят с помощью ваттметра и секундомера. Погрешность поверяемого (калибруемого) счетчика рассчитывают:
d =
![]() ´100%, (22)
´100%, (22)
где WП – значение электрической энергии по показаниям поверяемого (Алибруемого) счетчика. Для нее надо знать
С =
![]() , Вт с/об.,
, Вт с/об.,
где А – число оборотов диска, соответствующее энергии 1 кВт час, тогда
WП = C ´ N, (23)
где C – постоянная счетчика; N – число оборотов диска за время t0.
Если по показаниям эталонного ваттметра установить действительное значение мощности P0 и поддержать ее неизменной в течение времени t0 определяемого по эталонному секундомеру, то действительное значение энергии
W0 = P0 ´ t0. (24)
Выбор метода поверки и эталонов, с которыми производится сличение, выполняются в соответствии с государственной поверочной схемой.
Для чего разрабатываются поверочные схемы?
Для обеспечения правильной передачи размеров единиц измерения от эталона к рабочим средствам измерения составляют поверочные схемы, устанавливающие метрологические соподчинения государственного эталона, разрядных эталонов и рабочих средств измерений.
Поверочные схемы разделяют на государственные и локальные.
Государственные поверочные схемы распространяются на все средства измерений данного вида, применяемые в стране.
Локальные поверочные схемы предназначены для метрологических органов министерств, распространяются они также и на средства измерений подчиненных предприятий. Кроме того, может составляться и локальная схема на средства измерений, используемые на конкретном предприятии. Все локальные поверочные схемы должны соответствовать требованиям соподчиненности, которая определена государственной поверочной схемой (рисунок 6). Государственные поверочные схемы разрабатываются научно-исследовательскими институтами Госстандарта РФ, держателями государственных эталонов.
В некоторых случаях бывает невозможно одним эталоном воспроизвести весь диапазон величины, поэтому в схеме может быть предусмотрено несколько первичных эталонов, которые в совокупности воспроизводят всю шкалу измерений. Например, шкала температуры от 1,5 до 105 К воспроизводится двумя государственными эталонами. Государственные поверочные схемы утверждаются Госстандартом РФ, а локальные – ведомственными метрологическими службами или руководством предприятия.
Рассмотрим в общем виде содержание государственной поверочной схемы. Наименование эталонов и рабочих средств измерений обычно располагают в прямоугольниках (для государственного эталона прямоугольник двухконтурный). Здесь же указывают метрологические характеристики для данной ступени схемы. В нижней части схемы расположены рабочие средства измерений, которые в зависимости от их степени точности (т.е. погрешности измерений) подразделяют на пять категорий: наивысшей точности; высшей точности; высокой точности; средней точности; низшей точности. Наивысшая точность обычно соизмерима со степенью погрешности средства измерения государственного эталона.
В поверочной схеме уровни точности рабочих средств измерений определяются их погрешностями.
В каждой ступени измерений поверочной схемы регламентируется метод передачи размера единицы и его допускаемая погрешность.
Кроме наименования СИ указываются в прямоугольниках основные метрологические характеристики:
·
пределы измерений;
·
неисключенная составляющая систематической погрешности q0;
·
СКО случайной погрешности S0;
·
нестабильность воспроизведения ЕФВ n0;
·
доверительная погрешность d0;
абсолютная погрешность D.
Для государственных эталонов указывается НСП q0 и СКО S0. Основным показателем достоверности передачи размера единицы величины является соотношение погрешностей средств измерений между вышестоящей и нижестоящей ступенями поверочной схемы. В идеале это соотношение должно быть 1:10, однако на практике достичь его не удается, и минимально допустимым соотношением принято считать 1:3. Чаще они бывают 1:5; 1:4; 1:3. Чем больше величина этого соотношения, тем меньше уверенность в достоверности показаний измерительного прибора. При разработке конкретных поверочных схем
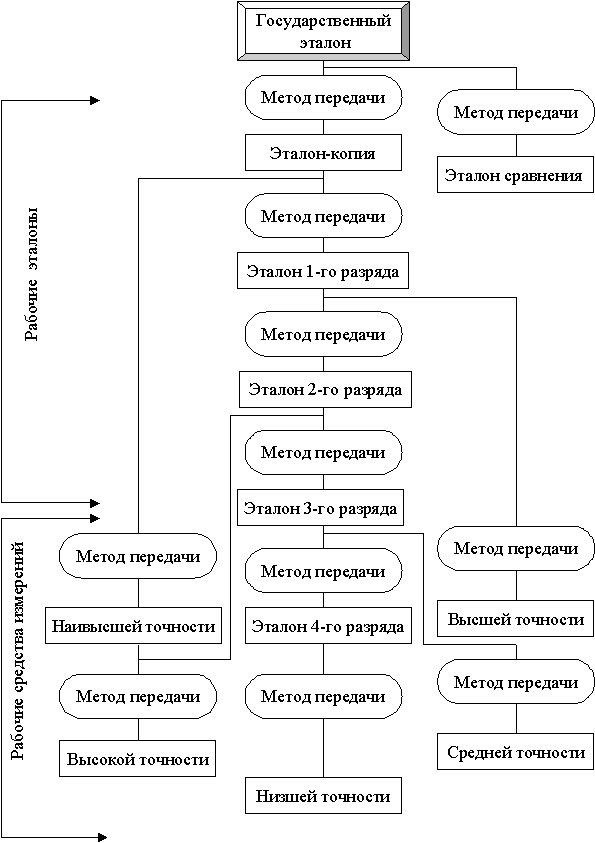
Рисунок 6 – Общий вид государственной поверочной схемы
необходимо следовать приведенной схеме. Строгое соблюдение поверочных схем и своевременная поверка разрядных (рабочих) эталонов – необходимые условия для передачи достоверных размеров единиц измерения рабочим средствам измерений.
Что такое межповерочный (межкалибровочный) интервал?
Межповерочным (межкалибровочным) интервалом называют календарный промежуток времени, по истечении которого средство измерения должно быть направлено на поверку (калибровку) независимо от его технического состояния. Различают три вида межповерочных (межкалибровочных) интервалов:
• первый вид – единый для всех средств измерений данного типа интервал, устанавливаемый на основе нормативных документов на этот вид средств измерений. В этом случае межповерочный (межкалибровочный) интервал определяется Госстандартом РФ при утверждении типа средства измерения по результатам испытаний. Величина интервала учитывает показатели метрологической безотказности и среднее значение времени использования средств измерений в нормальных условиях;
• второй вид – интервал, установленный в соответствии с конкретными условиями эксплуатации средств измерений данного типа в организациях и на предприятиях. Если назначенный интервал не совпадает с указанным интервалом в нормативных документах на данный тип средств измерений, его величину следует согласовать с Госстандартом или с аккредитированной им ведомственной метрологической службой. Для средств измерений, которые не подлежат госнадзору, межкалибровочный интервал определяется по решению метрологической службы юридического лица;
• третий вид — межповерочные (межкалибровочные) интервалы для средств измерений, предназначенных для ответственных измерительных операций, например, измерений, связанных с безаварийной работой атомных электростанций, газопроводов и т.п. Индивидуальные интервалы предусмотрены также для вторичных и разрядных эталонов. Третий вид интервалов связан с учетом календарного времени эксплуатации средств измерений, так как из-за старения их деталей и узлов возрастают погрешности, что обусловило сокращение межповерочных интервалов. Согласование назначенных интервалов аналогично описанному для второго вида. Общим для всех видов межповерочных (межкалибровочных) интервалов является учет показателей метрологической безотказности средств измерений, в частности, такой ее составляющей, как средняя наработка на метрологический отказ. Этот показатель может быть определен в процессе испытаний средства измерения, по результатам которого рассчитывают время достижения наименьшего заданного значения вероятности отказа. Это время и служит основой для установления межповерочного (межкалибровочного) интервала.
Межповерочный (межкалибровочный) интервал Тмп определяется исходя из вероятности безотказной в метрологическом смысле работы Pм(t) и вероятности метрологического отказа Pм.отк.:
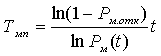 , (25)
, (25)
где t – время для которого определена вероятность безотказной работы Pм(t).
Значения Pм.отк. в зависимости от требований к измерениям варьируются так:
Pм.отк. = 0,2 … 0,1 при технических измерениях:
Pм.отк. = 0,15 … 0,05 при поверке (калибровке), градуировке;
Pм.отк. = 0,05 … 0,01 при особо ответственных измерениях.
Чем определяются необходимые для средств измерений виды
деятельности по обеспечению единства измерений?
Закон "Об обеспечении единства измерений" (2008 г.) разделяет весь парк средств измерений в стране на две сферы: сферу государственного регулирования b сферу рыночного регулирования.
Государственный метрологический контроль и надзор распространяется на:
• здравоохранение, ветеринарию, охрану окружающей среды, обеспечение безопасности труда; торговые операции и взаимные расчеты; обеспечение обороны государства;
• производство продукции, поставляемой по контрактам для государственных нужд в соответствии с законодательством Российской Федерации;
• испытания и контроль качества продукции в целях определения соответствия обязательным требованиям государственных стандартов Российской Федерации; обязательную сертификацию продукции, услуг и т.д. ГМК и Н в сфере обеспечения обороны страны предполагает проведение поверки средств измерений, применяемых при разработке, производстве и испытаниях оружия и военной техники, а также средств измерений военного назначения при их выпуске из производства.
В соответствии с Законом РФ "О техническом регулировании" обязательными являются требования государственных стандартов по обеспечению безопасности продукции, работ и услуг для окружающей среды, жизни, здоровья и имущества граждан, для обеспечения технической и информационной совместимости, взаимозаменяемости продукции, единства методов их контроля и маркировки, а также иные требования, установленные законодательством Российской Федерации. В этой связи должны подлежать государственному метрологическому контролю и надзору средства измерений, применяемые для контроля соответствия требованиям:
• к защитным устройствам, к характеристикам детских игрушек, одежды и обуви, к прочностным характеристикам элементов изделий и т.п.;
• к уровню и времени вредных воздействий (уровню шума, вибрации, радиационных и электромагнитных излучений, допустимым нормам давления на почву, величине предельно допустимых выбросов и концентраций вредных веществ и другим опасным и вредным свойствам);
• к материалам, используемым при изготовлении продукции (ограничений по химическому составу, ограничений на допустимый уровень содержания вредных и опасных веществ, микробиологических критериев безопасности, требований к воздухонепроницаемости, гигроскопичности, электролизуемости и др.);
• к правилам эксплуатации (применения) продукции, ее технического обслуживания и ремонта, невыполнение которых может угрожать безопасности.
Средства измерений, применяемые в перечисленных областях деятельности, должны пройти испытания с целью утверждения типа, первичную поверку, а затем подлежат периодическим поверкам. Для всех средств измерений, предназначенных для серийного производства или ввозимых по импорту большими партиями, необходимо проводить испытания с целью утверждения типа, так как заранее неизвестно, где будут использоваться эти средства измерений.
Во всех остальных случаях для обеспечения достоверности результатов измерений допускается проводить добровольную сертификацию и калибровку средств измерений.
Что такое погрешность результата измерений?
Любой результат измерений содержит погрешность из-за наличия погрешностей, присущих самому средству измерений, выбранным методу и методике измерений, из-за влияния внешних условий и других причин, вызывающих погрешности. Погрешность вычисляется или оценивается, или приписывается полученному результату.
Погрешность результата измерения – это отклонение результата измерения от истинного значения измеряемой величины.
Истинное значение величины остается неизвестным в связи с наличием погрешностей. На практике используется действительное значение величины, которое заменяет истинное значение.
Погрешность находят по формуле
Dxист = хизм – Х, (26)
где Dxист – погрешность измерения; Dxист – значение величины, полученное в результате измерения; Х – истинное значение величины.
Или Dxд = хизм – Хд, (27)
где Хд – значение величины, принятое за действительное.
Истинное значение величины познается только в результате бесконечно большого числа измерений с бесконечным совершенствованием методов и средств измерений, т. е. Dxд ®0, при n® ¥, где п — число измерений.
По формуле (2.2) находят абсолютную погрешность измерения, выражающуюся в единицах измеряемой величины.
Относительная погрешность измерения есть отношение абсолютной погрешности измерения к действительному значению измеряемой величины. Она выражается в долях значения измеряемой величины или в процентах. Относительную погрешность находят по формулам:
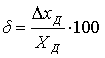 (28)
(28)
Например, если действительное значение массы Хд=10 кг, а абсолютное значение погрешности Dх==0,01 кг, то относительная погрешность составит
![]() или
или
![]() .
.
Использование относительных погрешностей в ряде случаев значительно удобнее, так как по значению относительной погрешности можно судить о качестве полученного результата.
Погрешности можно разделить по признакам:
·
по способу выражения – абсолютные и относительные;
·
по характеру проявления – систематические и случайные;
·
по условиям измерения измеряемой величины – погрешность воспроизведения единицы, хранения единицы, передачи размера единицы физической величины.
Какие погрешности называются систематическими
и на какие виды они подразделяются?
Систематическая погрешность измерения — составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. Эти погрешности могут быть в большинстве случаев изучены до начала измерений, и результат измерения может быть уточнен или путем внесения поправок, если числовые значения этих погрешностей определены, или путем использования таких способов измерений, которые дают возможность исключить влияние систематических погрешностей без их определения. Результаты измерений тем ближе к истинному значению, чем меньше оставшиеся не исключенные систематические погрешности.
По характеру проявления систематические погрешности подразделяются на постоянные, прогрессивные и периодические (рисунок 7).
Постоянные погрешности – погрешности, длительное время сохраняющие свое значение. Они встречаются наиболее часто. К постоянным относятся погрешности большинства мер (гирь, концевых мер длины), погрешности градуировки шкал измерительных приборов и др. Например, погрешность от постороннего груза на чашке весов, погрешность от неточной установки прибора на нуль.
Прогрессивные погрешности – непрерывно возрастающие или убывающие погрешности. К ним относятся погрешности от износа контактирующих деталей средств измерении, постепенное падение напряжения источника тока (аккумуляторных батарей), погрешность от постепенного прогрева измерительной аппаратуры и др.
Периодические погрешности – погрешности, периодически изменяющие значение и знак. Обычно эта погрешность встречается в угломерных приборах с круговой шкалой. Например, погрешность от эксцентриситета круговой шкалы и оси вращения стрелки средства измерений.
Погрешности, изменяющиеся по сложному закону, появляются вследствие действия нескольких систематических погрешностей.
Рисунок 7 – Виды систематических погрешностей:
а) постоянные; б) прогрессивные; в) периодические
Как можно уменьшить влияние систематических погрешностей?
При подготовке, проведении, обработки результатов измерений стараются в максимальной степени или исключить, или учесть влияние систематических погрешностей. Условно можно выделить четыре основные группы мероприятий:
·
устранение источников погрешностей до начала измерений
·
устранение погрешностей в ходе измерений;
·
внесение известных поправок в результат измерения;
·
оценка границ не исключенных систематических погрешностей.
Устранение источников погрешностей до начала измерений является наиболее рациональным, так как в этом случае существенно упрощается и словииется процесс измерений.
Оператор до начала работ устраняет источники погрешностей путем непосредственного их удаления (например, источника тепла), защиты измерительной аппаратуры и объекта измерений от влияния этих источников.
Инструментальные погрешности конкретного средства измерений могут быть устранены до начала измерений путем ремонта, регулировки. Погрешности измерений, возникающие из-за неправильной установки средств измерений, также можно устранить в большинстве случаев.
Погрешности измерений, возникающие вследствие влияния внешних полей, также стараются исключить всевозможными мерами. Например, влияние магнитного поля Земли устраняется устройством замкнутых и непрерывных экранов из магнитомягких. Материалов.
Погрешности, вызванные вредным влиянием сотрясений, вибраций, устраняются путем амортизирования средств измерений и их деталей. Для этого используют поглотители колебаний в зависимости от частоты этих колебаний и чувствительности средств измерений к этим влияниям. Например, устройство подкладок из губчатой резины к средствам измерений, различного рода подвесы (струны, пружины и т. Д.).
Следующим способом устранения систематических погрешностей является их исключение в процессе измерения. К достоинствам способа относится то обстоятельство, что нет необходимости применять какие-либо устройства и приспособления. Этим способом имеется возможность исключить инструментальные погрешности, погрешности от установки, погрешности от внешних влияний.
Наиболее распространенным способом исключения систематической погрешности является способ замещения, суть которого заключается в том, что измеряемый объект заменяют известной мерой, находящейся в тех же словииях. Например, при измерениях электрических параметров: сопротивления, емкости, индуктивности объект подключается к измерительной цепи. В большинстве случаев при этом пользуются нулевыми методами (мостовым, компенсационным и др.), при которых производится электрическое уравновешивание цепи. После этого, не меняя схемы, вместо измеряемого объекта включают меру переменного значения (магазин сопротивлений, емкости, индуктивности и
т. Д.) и, изменяя их значение, добиваются восстановления равновесия цепи.
В этом случае способом замещения исключается остаточная неуравновешенность мостовых цепей, влияния на цепь магнитных и электрических полей и др.
В ходе измерений оператор может исключить систематическую погрешность и способом компенсации ее по знаку, суть которого заключается в том, что измерения проводят дважды так, чтобы погрешность входила в результаты с противоположными знаками. Исключается она при вычислении среднего значения:
![]() , (29)
, (29)
где
![]() – среднее арифметическое значение измеряемой величины; х1, х2 – результаты измерений; хД – действительное значение измеряемой величины, Dс – систематическая погрешность.
– среднее арифметическое значение измеряемой величины; х1, х2 – результаты измерений; хД – действительное значение измеряемой величины, Dс – систематическая погрешность.
Характерным примером способа компенсации является исключение погрешности, обусловленной включением магнитного поля Земли. Первое измерение проводят, когда средство измерения находится в любом положении. Перед проведением второго средство измерений поворачивают в горизонтальной плоскости на 180°. Если в первом случае магнитное поле Земли, складываясь с полем средства измерений, вызвало положительную погрешность, то при повороте на 180° магнитное поле Земли будет оказывать противоположное действие и вызовет отрицательную погрешность по размеру, равному первой.
В некоторых случаях используется способ противопоставления, суть которого заключается в том, что измерение проводят 2 раза так, чтобы причина, вызывающая погрешность, при первом измерении оказала противоположное действие на результат второго. Рассмотрим его на примере взвешивания на равноплечих весах. Условие равновесия коромысла выглядит следующим образом:
m1 l2 = m211, (30)
где m1 — масса взвешиваемого груза; m2 — масса уравновешивающих гирь; l1 и l2 — соответствующие плечи коромысла. Влияние неравноплечности будет выглядеть в виде множителя (l2 / l1) или
m1 = (l2 / l1) m2, (31)
Если повторить взвешивание, поместив груз на чашу весов, на которой ранее были гири, получим
m'2 l1 = m112, (m'2 ¹ m'1) (32)
Разделив первое условие равновесия на второе, найдем, что
(m1 / m'2) = (m2 / m1), (33)
откуда
![]() (34)
(34)
Если m2 и m'2 лишь незначительно отличаются друг от друга, то
m1 = (m2 + m'2 )/2, т.е. влияние на результат неравноплечности весов окажется исключенным.
Для исключения прогрессирующего влияния какого-либо фактора, являющегося линейной функцией времени (например, постепенного прогрева аппаратуры, падения напряжения в цепи питания, вызванного разрядом аккумулятора и т. д.), применяется способ симметричных наблюдений. Такая функция может быть изображена в виде графика (рисунок 8). По оси абсцисс отложено время, а по оси ординат – прогрессивная погрешность.
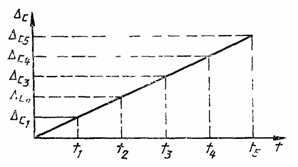
Рисунок 8 – Изменение прогрессивной систематической
погрешности во времени
Способ симметричных наблюдений заключается в том, что в течение некоторого интервала времени выполняется несколько измерений одной и той же величины постоянного размера и за окончательный результат принимается полусумма отдельных результатов, симметричных по времени относительно середины интервала.
![]() Рекомендуется использовать данный способ, когда не очевидна возможность существования прогрессивной погрешности. Если измерения не удалось организовать так, чтобы исключить или скомпенсировать какой-либо фактор, влияющий на результат, то в последний вводится поправка. Наиболее распространенным способом внесения поправок является алгебраическое сложение результата измерения и поправок Vi, с учетом ее знака. Поправка по числовому значению равна систематической погрешности и противоположна ей по знаку (аддитивная поправка) Dci = - V.
Рекомендуется использовать данный способ, когда не очевидна возможность существования прогрессивной погрешности. Если измерения не удалось организовать так, чтобы исключить или скомпенсировать какой-либо фактор, влияющий на результат, то в последний вводится поправка. Наиболее распространенным способом внесения поправок является алгебраическое сложение результата измерения и поправок Vi, с учетом ее знака. Поправка по числовому значению равна систематической погрешности и противоположна ей по знаку (аддитивная поправка) Dci = - V.
В некоторых случаях погрешность исключают путем умножения результата измерения на поправочный множитель, который может быть больше или меньше единицы (мультипликативная поправка)
В то же время, в ряде случаев исключение систематических погрешностей оказывается практически невозможным.
Систематические погрешности, остающиеся после введения поправок на ее наиболее существенные составляющие, включают в себя ряд элементарных составляющих, называемыми неисключенньши остатками систематических погрешностей. К их числу относят погрешности определения поправок, погрешности, зависящие от точности измерения влияющих величин, входящих в формулы для определения поправок, погрешности, связанные с колебаниями влияющих величин в столь малых пределах, что поправки на них не вводятся.
Что такое не исключенные систематические погрешности
и как они учитываются в результатах измерений?
Наибольшую опасность представляют не выявленные систематические погрешности, которые могут быть причиной ошибочных научных выводов, неудовлетворительной конструкции средств измерений и снижения качества продукции в производстве, поскольку существенно искажают результаты измерений.
Неисключенная систематическая погрешность - это составляющая погрешности результата измерений, обусловленная погрешностями вычисления и выведения поправок на влияние систематических погрешностей или же систематической погрешностью, поправка на действие которой не введена вследствие малости.
Неисключенная систематическая погрешность характеризуется ее границами. Границы не исключенной систематической погрешности при числе слагаемых n < 3 вычисляют по формуле
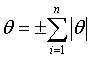 , (35)
, (35)
где Q – граница i-й составляющей не исключенной систематической погрешности.
При числе не исключенных систематических погрешностей n > 4 вычисления производят по формуле:
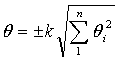 , (36)
, (36)
где k – коэффициент зависимости отдельных не исключенных систематических погрешностей от выбранной доверительной вероятности Р при их равномерном распределении (при Р = 0,99, k = 1,49; при Р = 0,95, k = 1,1; при Р = 0,90,
k = 0,95;).
Какие погрешности называются случайными?
Случайная погрешность измерения - это составляющая погрешности результата измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины. Эта погрешность возникает вследствие вариации показаний измерительного прибора, погрешности округления при отсчитывании показаний измерительного прибора, изменений условий измерения случайного характера и т. д. Случайные погрешности не поддаются исключению из результатов измерений, как систематические.
Как уменьшить влияние случайных погрешностей
на результат измерений?
Установлены два положения теории погрешностей:
1 – при большом числе измерений случайные погрешности одинакового числового значения, но разного знака встречаются одинаково часто;
2 – большие по абсолютному значению погрешности встречаются реже, чем малые.
Из этого следует, что при увеличении числа измерений случайная погрешность результата полученного из серии измерений уменьшается, так как погрешности компенсируют друг друга по знаку, и их сума стремится к нулю.
Какие характеристики используются для определения
случайных погрешностей измерений?
Согласно теории погрешностей проведение повторных измерений дает возможность, используя методы теории вероятности и математической статистики, уточнить результат, т. е. приблизить значение измеряемой величины к истинному ее значению.
Вследствие влияния случайных погрешностей результаты повторных измерений незначительно расходятся между собой. Максимально приближенным к истинному значению будет среднее арифметическое
![]() значение результатов измерений:
значение результатов измерений:
![]() , (37)
, (37)
где
![]() – результат наблюдения; п – число единичных наблюдений.
– результат наблюдения; п – число единичных наблюдений.
Случайные погрешности вызывают разброс результатов отдельных измерений и оцениваются характеристиками такого разброса (рассеивания) экспериментальных данных. Это рассеивание характеризуется параметрами:
1 – Размах результатов измерений (R): оценка рассеяния результатов единичных измерений физической величины, образующих ряд (или выборку из n измерений), вычисляемая по формуле: Rn = хmax – хmin, где хmax, хmin – наибольшее и наименьшее значения физической величины в данном ряду измерений;
2 – Средняя квадратическая погрешность результатов единичных измерений в ряду измерений (S): оценка рассеяния единичных результатов измерений в ряду равноточных измерений одной и той же физической величины около среднего их значения. Среднее квадратическое отклонение S результата единичного наблюдения, взятого из совокупности таких измерений, вычисляют по формуле:
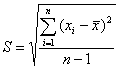 . (38)
. (38)
3 – Средняя квадратическая погрешность результата измерений (среднего арифметического) (Sx): оценка случайной погрешности среднего арифметического значения результата измерений одной и той же величины в данном ряду измерений. Среднее квадратическое отклонение S{x) результата измерения является параметром функции распределения и подсчитывается по формуле:
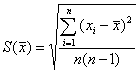 , (39)
, (39)
где
![]() – i-й результат наблюдения;
– i-й результат наблюдения;
![]() – среднее арифметическое исправленных результатов наблюдений (результат измерения); п – число наблюдений.
– среднее арифметическое исправленных результатов наблюдений (результат измерения); п – число наблюдений.
Из формул (2.1) и (2.2) следует, что точность среднего арифметического значения измеряемой величины в
![]() раз выше точности единичного наблюдения.
раз выше точности единичного наблюдения.
4 – Средняя арифметическая погрешность
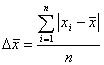 . (40)
. (40)
Какие погрешности называются грубыми?
Грубая погрешность измерения - это погрешность измерения, существенно превышающая ожидаемую погрешность при данных условиях. Результаты измерений, содержащие грубые погрешности, в расчет не берутся. Основными причинами этих погрешностей являются ошибки экспериментатора, резкое и неожиданное изменение условий измерения, неисправность прибора и др. Грубые погрешности не всегда легко обнаружить, для выявления грубых ошибок используют статистические методы.
Какие используются измерительные шкалы?
На практике используются шкала порядка, шкала интервалов и шкала отношений.
Шкала порядка представляет собой ранжированный ряд - упорядоченную последовательность размеров Q1< Q2< Q3<…< Qj<…, каждый из которых больше предыдущего, хотя сами размеры неизвестны. Если есть возможность опытным путем сравнить интересующий нас размер Qi, с одним из членов ранжированного ряда Qj, то экспериментальное решение неравенства Qi <> Qj, можно рассматривать как результат измерения, дающий некоторую количественную информацию о Qi. В соответствии с третьим постулатом метрологии решение о том, что i-ый размер меньше j-го либо больше или равен ему, носит случайный характер, т.е. выполняется с той или иной вероятностью, зависящей от силы неравенств. Решение (результат измерения) может оказаться ошибочным. При Qi>>Qj или Qi<<Qj вероятностью ошибки можно пренебречь. При Qi³Qj, Qi£Qj, и Qi»Qj с вероятностями ошибок нужно считаться. В таблице 4 приведен пример шкалы порядка
Таблица 4 – Шкала Бофорта для измерения силы ветра
|
Сила ветра, балл |
Название |
Признаки |
|
0 1 2 3 4 5 6 7 8 9 10 11 12 |
Штиль Тихий Легкий Слабый Умеренный Свежий Сильный Крепкий Очень крепкий Шторм Сильный шторм Жестокий шторм Ураган |
Дым идет вертикально Дым идет слегка наклонно Ощущается лицом, шелестят листья Развеваются флаги Поднимается пыль Вызывает волны на воде Свистит в вантах, гудят провода. На волнах образуется пена Трудно идти против ветра Срывает черепицу Вырывает деревья с корнем Большие разрушения Опустошительное действие |
После двух или более измерений, т.е. после сравнения Qi, с несколькими членами ранжированного ряда, измерительная информация на шкале порядка может быть представлена в виде:
Qi = Qi …Qj+1. (41)
Опорным (реперным) точкам j= 0, 1, 2, 3... на шкалах порядка принято ставить в соответствие баллы. С таким же успехом можно использовать буквенные обозначения или другие символы. Особенностью реперных шкал является то, что размеры Qj, образующие ранжированный ряд, как и интервалы между ними, неизвестны. Поэтому баллы ни складывать, ни вычитать, ни умножать, ни делить нельзя. На шкалах порядка не определены никакие математические операции.
В то же время, если один размер на шкале порядка больше другого, а последний в свою очередь больше третьего, то и первый размер больше третьего. Или если хоть один из двух размеров больше третьего, то их сумма тоже больше третьего размера. Если из двух размеров каждый меньше третьего, то меньше третьего размера и их разность. Эти свойства транзитивности означают, что на шкалах порядка определены (т.е. могут выполняться) логические операции.
Шкалы порядка являются наименее информативными из всех измерительных шкал. По ним не только нельзя определить, чему равен измеряемый размер Qi, но и невозможно сказать, на сколько (или во сколько раз) он больше или меньше размера Qj.
Наибольшее распространение шкалы порядка получили в областях, где к измерительной информации не предъявляется высоких требований. В промышленном производстве для измерений по шкалам порядка используются шаблоны.
Шкала интервалов служит для представления результатов измерений, полученных посредством экспериментального сравнения i-го размера с j-ым по правилу Qi – Qj=DQ. Сами размеры Qi и Qj остаются при этом неизвестными.
На рисунке 2. показано построение шкалы интервалов при j = 4. При выборе для сравнения 5-го, 6-го и больших размеров ноль на шкале интервалов DQ, получающийся при i = j, сместился бы выше, а при выборе 3-го, 2-го и меньших размеров - ниже показанного на рисунке. Таким образом, ноль на шкале интервалов не определен и зависит от выбора размера, с которым производится сравнение. Вследствие этого, по шкале интервалов можно установить, на сколько один размер больше другого, но нельзя сказать во сколько раз.
Рисунок 9 – Построение шкалы интервалов
По шкалам интервалов измеряются время, расстояние (если не известно начало пути), температура и многие другие На рисунке 9 приведены, например, температурные шкалы Цельсия, Реомюра, Фаренгейта и Кельвина. Первая и последняя из них разбиты на интервалы, равный 0.01 разности температур кипения воды и таяния льда при атмосферном давлении. Шкалы Реомюра и Фаренгейта разбиты на градусы, равные соответственно 1/80 и 1/180 этого интервала. По шкалам Цельсия и Реомюра сравнение ведется с температурой таяния льда, по шкале Фаренгейта - с температурой смеси льда с солью и нашатырем, по шкале Кельвина - с температурой, при которой прекращается тепловое движение молекул. На градуированных шкалах интервалов откладываются не размеры DQi а значения DQi, интервалов.
Шкалы интервалов являются более совершенными, чем шкалы порядка. На них определены аддитивные математические операции (сложение и вычитание), хотя и не определены мультипликативные (умножение и деление). Как следствие этого в экспериментальные данные, представленные на шкале интервалов, могут вноситься аддитивные поправки, в то время как использование поправочных множителей невозможно. Определить размер по шкале интервалов нельзя.
Шкала отношений служит для представления результатов измерений, полученных посредством экспериментального сравнения неизвестного размера Qi = Q с размером Qj=[Q] по правилу Q/[Q] = q. Числовое значение q показывает, во сколько раз измеряемый размер Q больше размера [Q], принятого за единицу измерения, или на сколько единиц он больше нуля.
На градуированных шкалах отношений откладываются не числовые значения q, а значения Q==q[Q] размеров Q. Градуированная шкала интервалов переходит в градуированную шкалу отношений при Qj®0; DQ®Qi=Q.
На рисунке 10 шкала Кельвина представляет собой уже шкалу отношений.
При практических измерениях на результат сравнения неизвестного размера Q с известным [Q] оказывает влияние множество (в том числе случайных) факторов. Поэтому на практике
![]() , (42)
, (42)
где отсчет x не только не равен числовому значению q, но, в отличие от последнего, представляет собой случайное число. Показание Х=х[Q] и результат измерения Q=vX+Q, получающийся после внесения в показание поправок n и Q, являются, следовательно, также случайными и не могут быть представлены точками на числовой оси Q.
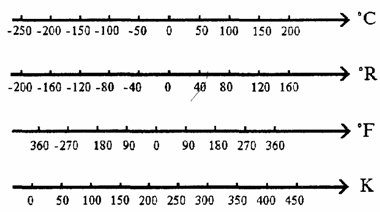
Рисунок 10 – Температурные шкалы Цельсия (°С), Реомюра (°R),
Фаренгейта (°F) и Кельвина (К)
Шкала отношений является самой совершенной и наиболее распространенной из всех измерительных шкал. Это единственная шкала, по которой можно установить значение измеренного размера. На шкале отношений определены любые математические операции, что и позволяет вносить в показания, нанесенные на шкалу, мультипликативные и аддитивные поправки.
Что представляют собой статистическо-вероятностные
характеристики результатов измерений?
Согласно третьему постулату метрологии из-за наличия случайных погрешностей результат измерения рассматривается как случайная величина.
Случайной называют величину, которая в результате опыта принимает значение заранее неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
В метрологии в ходе проведения измерений основное внимание уделяется закономерностям тех случайных явлений, которые обладают относительной устойчивостью некоторых свойств в их массовом проявлении. Такие случайные явления в массовом их проявлении в обыденной жизни встречаются довольно часто. Например, процент рождения мальчиков по отношению к общему числу рождения детей сохраняется довольно устойчиво (51,5%). Устойчивы также средние значения таких случайных явлений, как рост людей, месячная температура в определенных районах и т.п.
Явления, рассматриваемые в теории вероятностей, называются событиями. Проведение отдельного наблюдения, опыта или измерения называют испытанием. Его результат называют также событием. События принято обозначать первыми прописными буквами латинского алфавита: А, В, С…
Примеры событий: а) появление при измерении положительной случайной погрешности; б) «появление герба», «появление цифры» при бросании монеты.
Событие называют случайным (возможным), если в результате данного испытания оно может произойти, а может и не произойти Примеры случайных событий: величина и знак случайной погрешности результата измерения какой-либо величины; выигрыш в Спортлото, попадание в цель при выстреле.
При большом числе испытаний, производимых в одинаковых условиях, обнаруживаются вполне устойчивые закономерности, что является основой при применении методов теории вероятностей и математической статистики к обработке массовых наблюдений.
Случайное событие может появиться в результате испытаний, которые могут быть повторены любое число раз при одних и тех же условиях. Такое событие называется массовым. Оно может быть охарактеризовано числом, подсчитав его частость
![]() или относительную частоту, выражающуюся отношением числа появлений этого события к числу всех произведенных испытаний,
или относительную частоту, выражающуюся отношением числа появлений этого события к числу всех произведенных испытаний,
![]() =m/n. Например, произведено 20 измерений одной и той же величины, при этом положительных погрешностей оказалось 6. Следовательно, m=6, n=20, относительная частота появления положительной погрешности 6/20 = 0,3 или 30%.
=m/n. Например, произведено 20 измерений одной и той же величины, при этом положительных погрешностей оказалось 6. Следовательно, m=6, n=20, относительная частота появления положительной погрешности 6/20 = 0,3 или 30%.
Относительная частота (частость) подсчитывается после опыта и выражается или дробью или в процентах.
Изучение массовых случайных событий показало, что при определенных условиях некоторые из них происходят с тем более постоянной устойчивой частостью, чем больше число испытаний. Появлением этих закономерностей является свойство устойчивости относительной частоты однородных случайных событий, т. е. уменьшение разброса ее значений, получаемых в равных сериях испытаний, при увеличении числа испытаний в каждой серии
Выполнив большую серию испытаний, можно с высокой точностью предсказать результат других таких же серий испытаний.
Английский ученый К. Пирсон, определяя относительную частоту появления герба при бросании монеты 12000 и 24000 раз, получил значения этой частоты соответственно 0,5016 и 0,5005. Нетрудно предсказать, что частость должна составлять значение, равное 0,5.
При большом числе испытаний п относительная частота обнаруживает устойчивость, которая характеризует объективную связь между комплексом условий, в которых производится опыт, и событием.
С увеличением числа испытаний п в сериях колебания значений в разных сериях уменьшается, т. е. существует определенное значение относительной частоты, от которого она отклоняется в разных сериях испытаний в ту и другую сторону. Этой постоянной величиной является количественная мера степени объективной возможности появления события при одном опыте, называемая вероятностью события (р).
Вероятность р события А можно определить как отношение числа m случаев, благоприятствующих появлению события А, к числу п всех возможных случаев; при этом случаи предполагаются равновозможными, несовместными и единственно возможными.
![]() . (43)
. (43)
Иногда
![]() . (44)
. (44)
Из определения следует, что вероятность любого события А заключена между нулем и единицей
![]() . (45)
. (45)
Свойство относительной частоты – устойчивость. Впервые ее отразил
Я. Бернулли в виде теоремы. При числе испытаний п неограниченно большом с вероятностью, сколь угодно близкой к единице, относительная частота m/n события сколь угодно мало отличается от его вероятности в отдельном опыте.
Закон распределения вероятностей дискретной случайной величины, заданный в виде таблицы, называют рядом распределения. Для удобства восприятия ряда распределения строят графики. Для этого строят точки с координатами (xi, pi), а затем соединяют их отрезками. Полученная фигура называется многоугольником распределения или полигоном частот (рисунок 10).
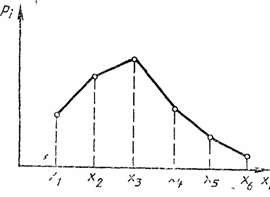
 Рисунок 10 – Полигон частот и функция плотности распределения
Рисунок 10 – Полигон частот и функция плотности распределения
Аналитически закон распределения задают обычно в виде функции
![]() и называют функцией распределения, которая является универсальной характеристикой случайной величины и существует для всех случайных величин – дискретных и непрерывных.
и называют функцией распределения, которая является универсальной характеристикой случайной величины и существует для всех случайных величин – дискретных и непрерывных.
Функции распределения вероятности для дискретных и непрерывных (аналоговых) величин имеют вид, показанный на рисунке 11.

а) б)
Рисунок 11 – Функции распределения вероятности случайных величин:
а) дискретной б) непрерывной
Наибольшее значение эмпирической функции распределения вероятности равно вероятности достоверного события, т.е. 1. Теоретическая функция распределения вероятности асимптотически приближается к единице.
Как определить вероятность попадания результата измерений
в заданный интервал?
Вероятность P того, что отдельный результат измерения окажется в интервале [x1; x2] равна площади криволинейной трапеции, ограниченной графиком плотности распределения вероятности p(x), осью абсцисс и перпендикулярами к ней на границах этого интервала (рисунок 12)
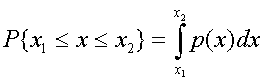

Рисунок 12 - Определение вероятности попадания отдельного значения в заданный интервал по плотности распределения вероятности
Функция распределения вероятностей случайной величины определят вероятность того, что случайная величина (отдельный результат измерения х) примет значение меньше ее аргумента. Следовательно, вероятность того, что
результат измерения окажется в интервале [x1; x2], равна разности значений F(x) на границах этого интервала (рисунок 13).
![]() . (46)
. (46)
 |
||||||
|
||||||
Рисунок 13 – Определение вероятности попадания отдельного значения в заданный интервал по функции распределения вероятности
Какова последовательность обработки результатов измерений?
Для повышения точности измерений, исключения ошибок и известных систематических погрешностей рекомендуется проводить измерения многократными наблюдениями, число которых должно быть не менее трех. Порядок обработки результатов прямых многократных измерений и оценки их погрешностей регламентирует ГОСТ. При статистической обработке результатов наблюдений выполняют операции:
·
исключают известные систематические погрешности из результатов наблюдений;
·
вычисляют среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения;
·
находят оценку среднего квадратического отклонения результата измерения;
·
устанавливают доверительные границы случайной погрешности результата измерения (при этом проверяют гипотезу о том, что результаты наблюдений принадлежат нормальному распределению);
·
исключают из ряда наблюдений грубые погрешности.
Как вычислить среднее арифметическое исправленных
результатов наблюдений?
Результат наблюдений, в который введены поправки с целью устранения систематических погрешностей, считается исправленным. Среднее арифметическое
![]() из полученных при измерении отдельных единичных наблюдений вычисляют по формуле:
из полученных при измерении отдельных единичных наблюдений вычисляют по формуле:
![]() , (47)
, (47)
где
![]() — результат наблюдения; п — число единичных наблюдений.
— результат наблюдения; п — число единичных наблюдений.
Если во всех результатах содержится постоянная систематическая погрешность, допускается исключать ее после вычисления среднего арифметического неисправленных результатов наблюдений.
Такая запись и подсчет
![]() удобно лишь при незначительном количестве исходных данных. В случае большого их количества целесообразно использовать другой способ.
удобно лишь при незначительном количестве исходных данных. В случае большого их количества целесообразно использовать другой способ.
Пусть произведено п испытаний, в которых случайная величина Х приняла
![]() раз значение
раз значение
![]() ,
,
![]() раз значение
раз значение
![]() ,
,
![]() раз значение
раз значение
![]() , причем
, причем
![]() . Тогда среднее значение случайной величины
. Тогда среднее значение случайной величины
![]() определится как среднее арифметическое этих значении:
определится как среднее арифметическое этих значении:
![]() (48)
(48)
или
![]() (49)
(49)
Отметим, что отношение
![]() есть частость появления значения Х (статистическая вероятность) и, обозначив каждое из них через
есть частость появления значения Х (статистическая вероятность) и, обозначив каждое из них через
![]() , получим
, получим
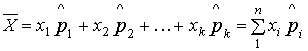 (50)
(50)
Например, пусть
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() . Найти
. Найти
![]() . Рассмат-ривая этот ряд величин, заметим, что три из них равны 20, одна — 22, одна — 24. Поэтому частота появления 20 равна 3, 22—1 и частота появления 24—1. Данные сведем в табл. 7.1.
. Рассмат-ривая этот ряд величин, заметим, что три из них равны 20, одна — 22, одна — 24. Поэтому частота появления 20 равна 3, 22—1 и частота появления 24—1. Данные сведем в табл. 7.1.
Таким образом,
![]()
При большом числе испытаний
![]() , где
, где
![]() — значение математической вероятности.
— значение математической вероятности.
Таблица 5
|
|
|
|
|
|
20 |
3 |
0,6 |
12,0 |
|
22 |
1 |
0,2 |
4,4 |
|
24 |
1 |
0,2 |
4,8 |
|
Итого |
5 |
1,0 |
21,2 |
С учетом этого формула (50) примет вид
![]() (51)
(51)
Эта формула используется в тех случаях, когда число членов вариационного ряда невелико. В тех случаях, когда используются интервальные ряды, т. е. группируют значения в интервалы, используют формулу
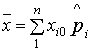 (52)
(52)
где
![]() — значение х в середине интервала.
— значение х в середине интервала.
Для облегчения вычислений при большом количестве интервалов удобно использовать метод произведений, приводящий к следующей формуле
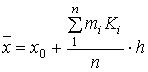 (53)
(53)
где
![]() — выбранное условное начало, обычно равное значению Х в середине интервала;
— выбранное условное начало, обычно равное значению Х в середине интервала;
![]() — значение, равное разности порядковых номеров между каждым интервалом, т е.
— значение, равное разности порядковых номеров между каждым интервалом, т е.
![]() ; h — ширина интервала.
; h — ширина интервала.
Таким образом, среднее значение дискретной случайной величины, полученное суммированием произведений всех ее возможных значений на их вероятности, называют математическим ожиданием и обозначают
![]() .
.
Среднее арифметическое значение
![]() будет приближаться к математическому ожиданию
будет приближаться к математическому ожиданию
![]() с увеличением числа испытаний в серии, т. е.
с увеличением числа испытаний в серии, т. е.
![]() , при
, при
![]() .
.
Математическое ожидание – это такая величина, около которой колеблется среднее значение случайной величины, найденное для каждой серии испытаний. В то же время математическое ожидание и среднее значение случайную величину характеризуют не полностью. Рассмотрим пример, в котором дискретные величины Х и Y заданы следующими законами распределения:
|
|
-0,04 |
+0,04 |
Y |
-100 |
+100 |
|
|
0,3 |
0,3 |
|
0,3 |
0,3 |
Математические ожидания этих величин равны:
![]() ;
;
![]() .
.
Математическое ожидание обеих случайных величин одинаково, а значения величин различны. Причем значения
![]() были ближе к математическому ожиданию, чем
были ближе к математическому ожиданию, чем
![]() . Таким образом, зная лишь математическое ожидание случайной величины, еще нельзя судить о возможных ее значениях и о том, как они отличаются друг от друга и как они группируются (рассеиваются) вокруг своего математического ожидания или среднего значения.
. Таким образом, зная лишь математическое ожидание случайной величины, еще нельзя судить о возможных ее значениях и о том, как они отличаются друг от друга и как они группируются (рассеиваются) вокруг своего математического ожидания или среднего значения.
Для более полной характеристики случайной величины используется такая характеристика как дисперсия
![]() , определяющая величину рассеивания случайной величины от ее математического ожидания.
, определяющая величину рассеивания случайной величины от ее математического ожидания.
Как вычислить дисперсию и среднее квадратическое
отклонение результата измерения?
Дисперсию можно определить по формуле
![]() . (54)
. (54)
В то же время такая характеристика не имеет широкого распространения из-за того, что имеет размерность квадрата случайной величины, а потому не дает желаемой наглядности. Значительно чаще используется среднеквадратическое отклонение случайной величины, равное значению корня квадратного из дисперсии
![]() . (55)
. (55)
Эта характеристика имеет размерность, совпадающую с размерностью случайной величины, и является более наглядной.
Среднее квадратическое отклонение S результата единичного наблюдения, взятого из совокупности таких измерений, вычисляют по формуле:
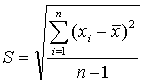 . (56)
. (56)
Среднее квадратическое отклонение S{x) результата измерения является параметром функции распределения и подсчитывается по формуле:
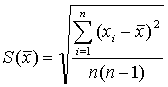 , (57)
, (57)
где
![]() – i-и результат наблюдения;
– i-и результат наблюдения;
![]() – среднее арифметическое исправленных результатов наблюдений (результат измерения); п – число наблюдений.
– среднее арифметическое исправленных результатов наблюдений (результат измерения); п – число наблюдений.
Из формул (56) и (57) следует, что точность среднего арифметического значения измеряемой величины в
![]() раз выше точности единичного наблюдения.
раз выше точности единичного наблюдения.
Что такое доверительный интервал результата измерения?
Доверительный интервал представляет собой интервал значений, в пределах которого с заданной вероятностью находится искомое значение результата измерений. Из-за наличия в результатах измерений случайных и не исключенных систематических погрешностей точное (истинное) значение измеряемой величины определить невозможно. Доверительный интервал является одной из форм представления результата измерений, учитывающий разброс экспериментальных данных.
Доверительные границы e (без учета знака) случайной погрешности измерения для результатов небольшого числа наблюдений (3<n<20), принадлежащих нормальному распределению, находят по формуле:
![]() , (58)
, (58)
где tp – коэффициент Стьюдента.
Коэффициент tp в зависимости от доверительной вероятности Р и числа результатов наблюдений п находят по таблице 6.
Таблица 6 – Значение коэффициента tp для доверительных границ
|
Число результатов |
Доверительная |
Число результатов |
Доверительная |
||||
|
0,9 |
0,95 |
0,99 |
0,9 |
0,95 |
0,99 |
||
|
2 |
2,92 |
4,30 |
9,92 |
12 |
1,78 |
2,28 |
3,06 |
|
3 |
2,35 |
3,18 |
5,84 |
14 |
1,76 |
2,15 |
2,98 |
|
4 |
2,13 |
2,78 |
4,60 |
16 |
1,75 |
2,12 |
2,92 |
|
5 |
2,02 |
2,57 |
4,03 |
18 |
1,73 |
2,10 |
2,88 |
|
6 |
1,94 |
2,48 |
3,71 |
20 |
1,72 |
2,09 |
2,85 |
|
7 |
1,90 |
2,37 |
3,50 |
22 |
1,72 |
2,07 |
2,82 |
|
8 |
1,86 |
2,31 |
3,36 |
25 |
1,71 |
2,06 |
2,79 |
|
9 |
1,83 |
2,26 |
3,25 |
30 |
1,70 |
2,04 |
2,75 |
|
10 |
1,81 |
2,23 |
3,17 |
∞ |
1,65 |
1,96 |
2,58 |
Окончательно полученный результат измерения записывают в виде:
![]() . (59)
. (59)
Для производственных измерений рекомендуется выбирать вероятность равную Р=0,9 и Р=0,95; для исследовательских целей и при ответственных лабораторных измерениях – Р=0,95 и Р=0,99.
Доверительные границы не исключенной систематической погрешности определяются по формуле:
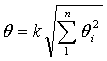 , (60)
, (60)
где qi – не исключенные систематические погрешности; k – коэффициент зависимости не исключенных систематических погрешностей.
Каким образом можно проверить является ли конкретное значение
результата измерений грубой погрешностью измерений (ошибкой)?
Промах – это погрешность результата отдельного измерения, которая для данных условий резко отличается от остальных результатов этого ряда. Иногда вместо термина "промах" применяют термин "грубая погрешность измерений"
При правильном проведении измерений отсутствуют грубые погрешности. Грубые погрешности и промахи возникают из-за неисправностей измерительных приборов, ошибок оператора, а также при кратковременных резких изменениях условий проведения измерений. Результаты измерений, содержащие грубые погрешности и промахи, отбрасываются. Для исключения из ряда наблюдений грубых погрешностей разработан ряд критериев (Райта, Романовского, Ирвина и др.). Наиболее простым, но грубым приемом является отбрасывание результатов наблюдений, содержащих погрешности, превышающие ±3S. Этим критерием можно пользоваться при числе наблюдений n>20. При малом объеме данных n он слабо отсеивает ошибки измерений.
Более точно проверить ошибку наблюдений при n<20 можно по критериям
![]() (критерию Романовского согласно ГОСТ 11.002—73) и
(критерию Романовского согласно ГОСТ 11.002—73) и
![]() (критерию Ирвина). Для того чтобы принять или исключить наиболее отклоняющиеся от остальных результатов наблюдения, находят отношение:
(критерию Ирвина). Для того чтобы принять или исключить наиболее отклоняющиеся от остальных результатов наблюдения, находят отношение:
![]() или
или
![]() , (61)
, (61)
где S — среднее квадратическое отклонение результата наблюдения по формуле (56).
Результат сравнивают с величиной
![]() , взятой из таблицы 4 для данного числа наблюдений п и принятого уровня значимости
, взятой из таблицы 4 для данного числа наблюдений п и принятого уровня значимости
![]() (
(
![]() =1—Р).
=1—Р).
Если
![]() или, то сомнительный результат наблюдений следует считать грубым и его надо отбросить. Затем вновь вычисляют х и S.
или, то сомнительный результат наблюдений следует считать грубым и его надо отбросить. Затем вновь вычисляют х и S.
Вышеуказанные способы обработки результатов наблюдений относятся к прямым измерениям.
Таблица 7 - Предельные значения β для исключения
грубых погрешностей
|
Число |
Предельные значения β при уровне значимости α |
Число |
Предельные значения β при уровне значимости α |
||||
|
0,1 |
0,05 |
0,025 |
0,1 |
0,05 |
0,025 |
||
|
3 |
1,15 |
1,15 |
1,15 |
10 |
2,03 |
2,18 |
2,29 |
|
4 |
1,42 |
1,46 |
1,48 |
12 |
2,13 |
2,29 |
2,41 |
|
5 |
1,60 |
1,67 |
1,72 |
14 |
2,21 |
2,37 |
2,50 |
|
6 |
1,73 |
1,82 |
1,89 |
16 |
2,28 |
2,44 |
2,58 |
|
7 |
1,83 |
1,94 |
2,02 |
18 |
2,34 |
2,50 |
2,66 |
|
8 |
1,91 |
2,03 |
2,13 |
20 |
2,38 |
2,56 |
2,71 |
|
9 |
1,98 |
2,11 |
2,21 |
- |
- |
- |
- |
При n>20 предельно допустимое значение tr определяется по формуле:
![]() , (62)
, (62)
где tP/2 – квантиль нормированной функции Лапласа для доверительной вероятности P.
Проверяемое значение xi является промахом, если выполняется неравенство umax≥tr, и его надо отбросить.
При большом числе измерений для определения промахов можно также применять критерий Шарлье. Значение нормированной функции Лапласа:
![]() . (63)
. (63)
По таблице критерия Шарлье определяется предельно допустимое значение КШ.
Промахом считается результат xi, для которого выполняется неравенство:
![]() , (64)
, (64)
где
![]() - среднее арифметическое значение результатов измерений;
- среднее арифметическое значение результатов измерений;
S – СКО результатов измерений.
Таблица 8 – Значения критерия Шарлье
|
n |
5 |
10 |
20 |
30 |
40 |
50 |
100 |
|
KШ |
1,3 |
1,65 |
1,96 |
2,13 |
2,24 |
2,32 |
2,58 |
Каковы правила округления результатов измерений?
1. Погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2, и одной – если первая цифра равна 3 или более.
2. Результат измерения округляется до того же десятичного знака, которым оканчивается округленное значение абсолютной погрешности. Если десятичная дробь в числовом значении результата измерений оканчивается нулями, то нули отбрасываются до того разряда, которым соответствует разряду числового значения погрешности.
3. Если цифра старшего из отбрасываемых разрядов меньше 5, то остальные цифры числа не изменяются. Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются.
4. Если цифра старшего из отбрасываемых разрядов больше или равна 5 (но за ней следуют отличные от нуля цифры), то последнюю сохраняемую цифру увеличивают на единицу.
5. Если отбрасываемая цифра равна 5, а следующие за ней цифры не известны или нули, то последнюю сохраняемую цифру числа не изменяют, если она четная и увеличивают на единицу, если она нечетная.
6. Округление производится лишь в окончательном ответе, а все предварительные вычисления производят с одним или двумя лишними знаками.
7. Погрешность округления не должна превышать 5% от погрешности измерений.
Какие показатели определяют качество результатов измерений?
Качество измерений характеризуется точностью, достоверностью, правильностью и сходимостью результатов.
Точность характеризуется рассеянием результата измерения около среднего значения. Мерой точности служит среднее квадратическое отклонение показания σx. Чем оно меньше, тем выше точность, так что этот показатель связан с качеством результата измерения обратной зависимостью.
Достоверность характеризует степень доверия к результатам измерений. Достоверность оценки погрешностей определяют на основе законов теории вероятностей и математической статистики.
Правильность – это качество измерений, отражающее близость к нулю систематических погрешностей.
Сходимость – это качество измерений, отражающее соответствие результатов измерений, выполняемых в одинаковых условиях. Сходимость показывает влияние случайных погрешностей.
Для сопоставления и совместного использования результатов измерений применяют единообразные показатели точности измерений и единые унифицированные формы представления результатов измерений. Количественные показатели точности измерений и способы их выражения устанавливает ГОСТ. При измерении различных величин и параметров в сельскохозяйственном производстве в качестве показателя точности обычно используют интервал, в котором погрешность измерения находится с заданной вероятностью.
Какова последовательность обработки результатов измерений?
Для уменьшения случайной составляющей погрешности, повышения точности измерений, исключения ошибок и известных систематических погрешностей рекомендуется проводить измерения многократными наблюдениями, число которых должно быть не менее четырех. Порядок обработки результатов прямых многократных измерений и оценки их погрешностей регламентирует ГОСТ. При статистической обработке результатов наблюдений должны быть выполнены следующие операции:
·
исключены известные систематические погрешности из результатов наблюдений;
·
исключены из ряда наблюдений грубые погрешности;
·
вычислено среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения;
·
найдено оценка среднего квадратического отклонения результата наблюдения и измерения;
·
проверена гипотеза о том, что результаты наблюдений принадлежат нормальному распределению;
·
установлены доверительные границы случайной погрешности результата измерения);
·
установлены границы не исключенных систематических погрешностей (НСП);
·
установлено, какие погрешности (случайные, НСП) необходимо учитывать в расчете границ доверительного интервала;
·
рассчитан доверительный интервал измеряемой величины.
В какой форме должен быть представлен результат измерений?
Для сопоставления и совместного использования результатов измерений применяют единообразные показатели точности измерений и единые унифицированные формы представления результатов измерений.
При симметричной доверительной погрешности результаты измерений представляют в форме доверительного интервала:
![]() (65)
(65)
где
![]() – результат измерения в единицах измеряемой величины;
– результат измерения в единицах измеряемой величины;
![]() и Р – погрешность измерения и установленная вероятность, с которой погрешность измерения находится в этих границах.
и Р – погрешность измерения и установленная вероятность, с которой погрешность измерения находится в этих границах.
Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности
![]() .
.
Если отсутствуют данные о виде функций распределений составляющих погрешности результата и нет необходимости дальнейшей обработки результатов или анализа погрешностей, то результаты представляют в форме:
![]() (66)
(66)
где
![]() – оценка среднего квадратического отклонения результата измерения; п – число результатов наблюдений;
– оценка среднего квадратического отклонения результата измерения; п – число результатов наблюдений;
![]() – границы не исключенной систематической погрешности результата измерений.
– границы не исключенной систематической погрешности результата измерений.
При прямых однократных измерениях исправными средствами точность оценивают пределами допускаемой основной и дополнительной погрешностей, и результат представляют в форме интервальной оценки:
![]() (67)
(67)
где
![]() – показание прибора;
– показание прибора;
![]() и Р – пределы допускаемой основной и дополнительной абсолютных погрешностей измерения и вероятность ее оценки.
и Р – пределы допускаемой основной и дополнительной абсолютных погрешностей измерения и вероятность ее оценки.
Пределы допускаемых погрешностей показаний при измерении нелинейных величин (давления, разрежения, температуры, расхода и т. п.) устанавливают по классам точности средств измерений в соответствии с ГОСТ. Пределы допускаемой погрешности измерения линейных размеров устанавливают для конкретных средств измерений с учетом условий их применения. Доверительная вероятность оценки погрешностей в указанных границах составляет при этом Р = 0,95.
С какой целью и как строится гистограмма?
Гистограмма является графическим изображением распределения вероятности экспериментальных данных. Построение гистограммы необходимо для наглядного представления распределения эмпирической вероятности с целью определения соответствующего теоретического закона распределения вероятности. Гистограмма представляет собой ступенчатую фигуру, состоящую из прямоугольников, основанием которых является ширина интервала h, а высотой – относительная частота mi/n или величина mi/(n· h).
Гистограмма строится в следующем порядке:
-
все экспериментальные данные упорядочиваются в вариационный ряд по мере увеличения их значений;
-
вариационный ряд результатов измерений разбивают на r интервалов: при n=50…100, r=7…9; при n=100…500, r=8…12;
-
рассчитывают ширину интервала h=( xmax- xmin)/r;
-
устанавливают границы интервалов: [xmin; xmin+h], [xmin+h; xmin+2h], [xmin+2h; xmin+3h],…, [xmin+(r-1)h; xmax];
-
- подсчитывают абсолютную частоту mi - число экспериментальных данных, попавших в каждый i-й интервал;
-
рассчитывают относительные частоты:
![]() ; (68)
; (68)
-
рассчитывают величину mi/(n· h);
-
строят гистограмму, отложив по оси абсцисс ширину интервалов h, по оси ординат – величину pэi или mi/(n· h) для каждого i-го интервала.
Для чего необходимо определять соответствие эмпирического распределения нормальному теоретическому закону?
Проверка соответствия эмпирического распределения нормальному теоретическому выполняется для повышения достоверности определения доверительного интервала.
Доверительные границы рассчитываются с помощью коэффициента Стьюдента tP, значения которого установлены, исходя из нормального распределения экспериментальных данных. Если же таким образом рассчитать доверительный интервал для распределений данных, существенно отличающихся от нормального, то вероятность попадания результатов измерений в границы доверительного интервала будет отличаться от принятой доверительной вероятности. Как показано на рисунке 14, она может быть меньше заданной (кривая 3), а может быть больше (кривая 2). Это будет влиять на оценку измеренной величины.
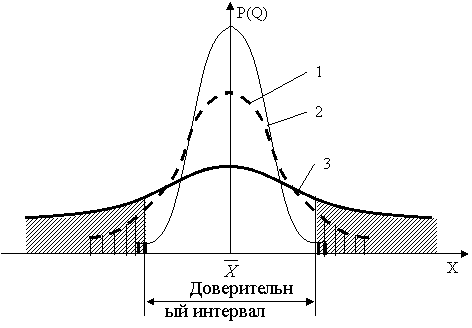
Рисунок 14 – График плотности распределения вероятности нормального (1) и распределений, отличных от нормального (2,3)
Как определить соответствие эмпирического распределения нормальному теоретическому закону?
Гипотеза о соответствии эмпирического распределения нормальному теоретическому закону проверяется с помощью критериев согласия Пирсона χ2, составного критерия, критерия Колмогорова-Смирнова, Мозеса-Смирнова, приближенных методов оценки и др.
Критерий Пирсона χ2 применяется для большого числа экспериментальных данных (n>50).
Составной критерий используется при малом числе экспериментальных данных (n≤50).
Критерий Колмогорова-Смирнова позволяет оценить не только соответствие эмпирического распределения теоретическому закону, но и определить, относятся ли две сравниваемые выборки к одной генеральной совокупности, т.е. сопоставить их вероятностные характеристики.
Критерий Мозеса-Смирнова Ώ2 применяется, если проверка по другим критериям не дала однозначного решения. Например, для разных уровней значимости получены разные выводы.
Приближенные методы сопоставляют эмпирическое и теоретическое распределения, сравнивая их точечные характеристики.
Как применять критерий Пирсона χ2?
Статистикой критерия Пирсона χ2 являются разности эмпирической и еоретической абсолютных частот. Порядок проверки гипотезы по критерию Пирсона χ2:
1.
Строится гистограмма по исправленным экспериментальным данным. В каждый из интервалов гистограммы должно входить не менее пяти данных. В противном случае такой интервал объединяется с соседним.
2.
Рассчитываются:
-
среднее арифметическое значение:
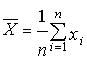 , (69)
, (69)
где xi - значение i-го результата измерений; n - число измерений;
-
среднее квадратическое отклонение (СКО):
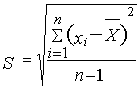 (70)
(70)
3.
Вычисляется вероятность pi попадания результата измерений в каждый из интервалов гистограммы [xk-1; xk] при нормальном законе распределения, используя функцию Лапласа Ф(t):
pi=Ф[(xиi-
![]() )/S] - Ф[(xнi-
)/S] - Ф[(xнi-
![]() )/S], (71)
)/S], (71)
где xиi, xнi – верхняя и нижняя границы i-го интервала;
Ф(**) – табличные значения функции Лапласа.
4.
Вычисляется показатель разности частот
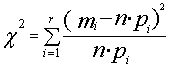 ; (72)
; (72)
5.
Проверяется выполнение неравенства c2<ca2, где ca2 – табличное значение c2 для уровня значимости a и числа степеней свободы (r-3) по таблице распределения c2. Если неравенство не выполняется, то гипотезу о нормальности эмпирического распределения отвергают. При этом вероятность, с которой эмпирическое распределение соответствует нормальному теоретическому, можно определить по критерию Колмогорова-Смирнова.
Как проверить соответствие нормальному распределению, пользуясь составным критерием?
Критерий состоит из двух частей. Гипотеза о нормальности эмпирического распределения принимается, когда выполняются 1-й и 2-й критерии (части).
Общий уровень значимости по критерию:
Q = q1 + q2, (73)
где q1 и q2 – уровни значимости по первой и второй частям критерия.
Критерий 1 проверяет общую форму распределения, оценивая среднее значение квантилей:
![]() , (74)
, (74)
где S* -смещенная оценка СКО:
![]()
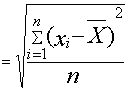
![]() ; (75)
; (75)
Критерий 1 выполняется, если значение d удовлетворяет условию:
:
![]() £
£
![]() <
<
![]() ,(76)
,(76)
где q1 – выбранный уровень значимости;
![]()
![]() ,
,
![]() - табличные значения, определяемые для вероятностей (1-q1/2) и q1/2.
- табличные значения, определяемые для вероятностей (1-q1/2) и q1/2.
Тогда переходят к проверке по критерию 2. В противном случае критерий 2 не рассчитывают, а гипотезу отклоняют, либо определяют, например, по критерию Колмогорова-Смирнова вероятность, с которой можно принять гипотезу.
Критерий 2 дополнительно проверяет «концы» распределения, т.е. большие отклонения от среднего значения.
По таблице критерия 2 определяют доверительную вероятность P в зависимости от уровня значимости q2, и числа экспериментальных данных n.
Рассчитывают значение функции Лапласа:
P/2=Ф(tP/2). (77)
Определяют значение квантили tP/2 по таблице функции Лапласа Ф(t).
Рассчитывают предельно допустимое отклонение от среднего значения:
Εmax=S×tP/2. (78)
Сравнивают все отклонения от центра распределения
![]() со значением εmax. Подсчитывают число m значений xi, для которых
со значением εmax. Подсчитывают число m значений xi, для которых
![]() > εmax.
> εmax.
Если это количество не более 1 для 10£n<20 или не более 2 для 20£n£50, то гипотеза по критерию 2 принимается.
Как применять критерий Колмогорова-Смирнова?
По критерию Колмогорова-Смирнова сравнивают эмпирические и теоретические значения интегральной функции распределения вероятностей.
Рассчитывают накопленные частоты для каждого из интервалов эмпирического распределения:
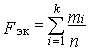 , (79)
, (79)
где mi - абсолютные частоты в интервалах с 1-го по k-й ;
Определяют теоретическую вероятность pi попадания результата измерений в каждый из интервалов при нормальном распределении, используя функцию Лапласа и рассчитывают накопленные частоты теоретического распределения:
![]() ; (80)
; (80)
Определяют наибольшую из разностей теоретической и эмпирической накопленных частот по интервалам: D = max½ Fэk - Fтk ½; (81)
Рассчитывают l = D×
![]() ; (82)
; (82)
Определяют вероятность P(l) по таблице 9. Если эта вероятность мала, то гипотезу отбрасывают.
Таблица 9 - Распределение критерия Колмогорова
|
λ |
P(λ) |
λ |
P(λ) |
λ |
P(λ) |
|
0,0 0,1 0,2 0,3 0,4 0,5 0,6 |
1,000 1,000 1,000 1,000 0,997 0,964 0,864 |
0,7 0,8 0,9 1,0 1,1 1,2 1,3 |
0,711 0,544 0,393 0,270 0,178 0,112 0,068 |
1,4 1,5 1,6 1,7 1,8 1,9 2,0 |
0,040 0,022 0,012 0,006 0,003 0,002 0,001 |
При числе результатов наблюдений n<15 принадлежность их к нормальному закону не проверяют.
Как применять критерий Мозеса-Смирнова?
Критерий Мозеса-Смирнова
![]() 2 применяют в следующей последовательности.
2 применяют в следующей последовательности.
1. Все экспериментальные данные упорядочивают в вариационный ряд по мере возрастания их значений:
![]() . (83)
. (83)
2. Определяют значения теоретической вероятности для каждого экспериментального данного
![]() по таблице функции Лапласа
по таблице функции Лапласа
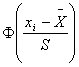 .
.
3. Рассчитывают значение функции теоретического распределения вероятности:
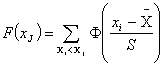 . (84)
. (84)
4. Рассчитывают значение
![]() :
:
![]() , (85)
, (85)
где j – номер экспериментального данного в вариационном ряду.
5. По таблице распределения
![]() находят значение функции «
находят значение функции «
![]() », соответствующее вычисленному значению
», соответствующее вычисленному значению
![]() .
.
6. Задают уровень значимости q, равный 0,1 или 0,2.
7. Принимают гипотезу о соответствии нормальному распределению, если
![]() q . (86)
q . (86)
Как оценить соответствие эмпирического и нормального распределений, пользуясь приближённым методом?
Приближённый метод оценки соответствия нормальному распределению учитывает расхождение характеристик асимметрии и эксцесса эмпирического и нормального теоретического распределений.
1. Рассчитывают для эмпирического распределения асимметрию
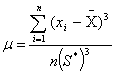 , (87)
, (87)
коэффициент эксцесса
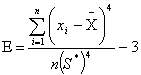 , (88)
, (88)
где S*- смещённая оценка СКО:
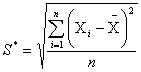 . (89)
. (89)
2. Вычисляются средние квадратические погрешности
асимметрии
![]() ; (90)
; (90)
эксцесса
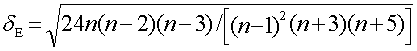 . (91)
. (91)
3. Оценивается расхождение теоретических и эмпирических характеристик:
если
![]() и
и
![]() близки к 0 или превышают это значение не более, чем на 2
близки к 0 или превышают это значение не более, чем на 2
![]() 3 среднеквадратические погрешности, то гипотеза о соответствии нормальному распределению принимается.
3 среднеквадратические погрешности, то гипотеза о соответствии нормальному распределению принимается.
Как получить результат косвенных измерений?
По исправленным результатам измеренных аргументов рассчитывают на основании функциональной зависимости для измеряемой величины A A=f(a1,a2,¼,am) оценку среднего значения
![]() , СКО среднего S(
, СКО среднего S(
![]() ), доверительные границы и доверительный интервал. Для этого установлено три алгоритма статистической обработки:
), доверительные границы и доверительный интервал. Для этого установлено три алгоритма статистической обработки:
1.
При отсутствии корреляции между погрешностями измеренных аргументов и линейной зависимости измеряемой величины от измеряемых аргументов A=b1×a1+ b2×a2+¼+ bm×am, (92)
где b1,b2, ¼, bm - постоянные коэффициенты
2.
При отсутствии корреляции между погрешностями измеренных аргументов и нелинейной зависимости измеряемой величины от измеряемых аргументов A=f(a1,a2,¼,am).
3.
При наличии корреляции между погрешностями измеренных аргументов.
Для расчета по первым двум алгоритмам необходимо определить для измеренных значений аргументов aj:
-
средние арифметические значения:
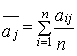 , (93)
, (93)
где n - число измерений аргумента aij;
-
СКО среднего для каждого измеренного аргумента:
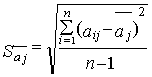 ; (94)
; (94)
-
проверить гипотезу о соответствии эмпирического распределения результатов измерений каждого аргумента теоретическому нормальному распределению вероятности.
Как установить, есть ли корреляция между погрешностями измеренных аргументов?
Критерием наличия корреляционной связи между результатами измерений аргументов является выполнение неравенства:
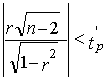 , (95)
, (95)
где t¢p - коэффициент Стьюдента для заданной доверительной вероятности и числа степеней свободы f=n-2;
rh,j – коэффициент корреляции между результатами измерений аргументов ah и aj:
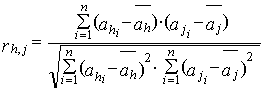 , (96)
, (96)
где
![]() ,
,
![]() - результаты i-го измерения h-го и j-го аргументов.
- результаты i-го измерения h-го и j-го аргументов.
Как получить значение косвенно измеряемой величины при ее линейной зависимости от измеренных аргументов и отсутствии
корреляции между ними?
Линейную зависимость измеряемой величины можно представить в общем виде:
![]() , (97)
, (97)
где bj – постоянные коэффициенты, установленные теоретически или экспериментально.
Применяется следующий порядок статистической обработки.
1.
Рассчитывается оценка среднего измеряемой величины:
![]() . (98)
. (98)
2.
Рассчитывается СКО оценки среднего измеряемой величины:
![]() . (99)
. (99)
3.
Определяется доверительная граница случайной погрешности:
![]() , (101)
, (101)
где tP – коэффициент Стьюдента для заданной доверительной вероятности P и числа степеней свободы f:
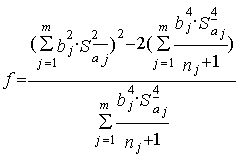 , (102)
, (102)
где nj - число измерений aj-го аргумента.
4.
Определяется, при необходимости доверительная граница НСП:
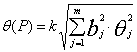 , (103)
, (103)
где
![]() - граница НСП j-го аргумента.
- граница НСП j-го аргумента.
5.
Оценивается соотношение случайных и не исключенных систематических погрешностей и определяется, какие погрешности должны быть учтены при определении границ Δ доверительного интервала.
6.
Рассчитывается доверительный интервал:
![]() . (104)
. (104)
Как получить значение косвенно измеряемой величины при ее нелинейной зависимости от измеренных аргументов и отсутствии корреляции между погрешностями их измерений?
Нелинейную зависимость измеряемой величины линеаризуют азложениием в ряд Тейлора:
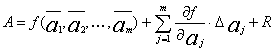 , (105)
, (105)
где
![]() - частная производная первого порядка по aj-му аргументу;
- частная производная первого порядка по aj-му аргументу;
Δ aj – наибольшие отклонения результата измерений aj-го аргумента от его среднего значения:
![]() ; (106)
; (106)
R – остаточный член ряда Тейлора.
Под остаточным членом ряда Тейлора R объединяются частные производные второго и более высоких порядков. Если отбросить R, округлив ряд на его величину, то в результатах измерений будет содержаться не исключенная систематическая методическая погрешность. Влияние и учет этой погрешности в результате измерений необходимо оценить. На основании этого устанавливается следующий порядок статистической обработки.
1.
Рассчитывается оценка среднего измеряемой величины:
![]() . (107)
. (107)
2.
Рассчитывается СКО оценки среднего измеряемой величины, характеризующее случайную погрешность измерений:
:
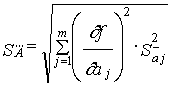 . (108)
. (108)
3.
Рассчитывается остаточный член ряда Тейлора R, характеризующий НСП:
![]() , (109)
, (109)
где
![]() - полный дифференциал второго порядка функции измеряемой величины.
- полный дифференциал второго порядка функции измеряемой величины.
Дифференциалы более высоких порядков при расчете R не учитываются, т.к. предполагается, что они не оказывают на результат существенного влияния.
4.
Оценивается влияние остаточного члена ряда R на результат измерений: на основании сопоставления характеристик случайных погрешностей и НСП:
Если R<0,8×
![]() , то R не влияет на результат измерений, и его можно отбросить. В противном случае R надо учесть в окончательном результате измерений при определении доверительной границы Δ.
, то R не влияет на результат измерений, и его можно отбросить. В противном случае R надо учесть в окончательном результате измерений при определении доверительной границы Δ.
5.
Рассчитывается доверительная граница Δ.
6.
Рассчитывается доверительный интервал по формуле (104).
Как получить значение косвенно измеряемой величины при наличии корреляции между погрешностями измеренных аргументов?
В случае корреляции между погрешностями измеряемых аргументов для статистической обработки результатов косвенных измерений используется метод приведения. Метод аналогичен порядку статистической обработки результатов прямых многократных измерений и не учитывает закон распределения экспериментальных данных.
1.
Рассчитываются значения измеряемой величины для соответствующих значений измеренных аргументов:
Aj=f(a1j,a2j,¼,amj). (110)
2.
Определяется оценка среднего арифметического значения измеряемой величины:
 .(111)
.(111)
3.
Рассчитывается СКО оценки среднего измеряемой величины:
-
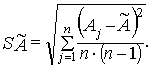
![]() (112)
(112)
4.
Рассчитываются доверительные границы Δ и доверительный интервал результата измерений по формуле:
![]() . (113)
. (113)
Что такое частные и полные погрешности измерений?
Различие между частными и полными погрешностями заключается в полноте охвата измерительной задачи. Оба вида погрешностей относятся к косвенным измерениям.
Погрешности измеренных аргументов называются частными. Они определяют полные погрешности, т.е. погрешности измеряемой величины.
Например, при измерении напряжения в электрической цепи по зависимости U=I·R погрешности измерения силы тока I и электрического сопротивления R являются частными. Они обуславливают полную погрешность измеряемого напряжения U:
![]() , (114)
, (114)
где δU, δI, δR – относительные погрешности физических величин напряжения, силы тока и сопротивления.
Как получить результаты совокупных и совместных измерений?
При совместных или совокупных измерениях результаты определяются из системы уравнений вида: ai×X+bi×Y+ci×Z=li,
где ai, bi, ci, li - непосредственно измеряемые величины; X, Y, Z - искомые величины.
В результате измерений получают n условных уравнений, которые необходимо привести к системе нормальных уравнений:
[aa]x+[ab]y+[ac]z=[al];
[ab]x+[bb]y+[bc]z=[bl]; (115)
[ac]x+[bc]y+[cc]z=[cl],
где
![]()
![]() ;
;
![]() ;
;
![]() . (116)
. (116)
Аналогично для остальных уравнений системы.
Как правило, получаемые условные уравнения являются неравноточными из-за различия внешних влияющих факторов, числа измерений, мер, используемых для сравнения. Это учитывается разными весовыми коэффициентами pi=1/S2, где S - СКО погрешности измерений условного уравнения. На величину pi умножаются коэффициенты нормальных уравнений a, b, c, l, и рассчитываются их суммы:
![]()
![]() ;
;
![]() ;
;
![]() и т.п.
и т.п.
Вычисляют оценки искомых величин: x=Da/D; y=Db/D;z=Dc/D,где
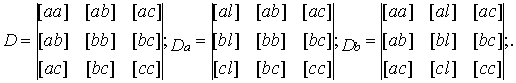
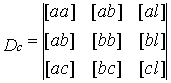 (117)
(117)
Вычисляют остаточные погрешности: v1=a1x+b1y+c1z-l1;
v2=a2x+b2y+c2z-l2;
. . . . . . . . . . . . . . . . (118)
vn=anx+bny+cnz-ln.
Рассчитывают СКО остаточных погрешностей:
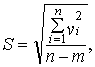 (119)
(119)
где m - число искомых величин.
Рассчитывают СКО искомых величин:
![]()
![]()
![]() (120)
(120)
где
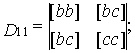
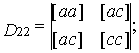
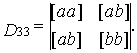 (121)
(121)
Рассчитывают доверительный интервал для каждой искомой величины:
x-tp×Sx<X<x+ tp×Sx; y- tp×Sy<Y<y+ tp×Sy; z- tp×Sz<Z<z+ tp×Sz, (122)
где tp - коэффициент Стьюдента для заданной доверительной вероятности и числе степеней свободы f=n-m.