Как мы знаем, для расчётов на статическую прочность необходимо предварительно экспериментально определить (или знать) механические характеристики материала, из которого изготовлена деталь, без чего невозможно составить условие прочности. По аналогии для расчётов на выносливость необходимо также экспериментально определить характеристику сопротивления усталости. Для определения этих характеристик используются специальные машины для усталостных испытаний. На машинах испытываются партии по 50 – 100 штук специальных гостированных образцов. В практике используются различные схемы нагружения образцов. Рассмотрим один из широко распространённых способов нагружения – изгиб с вращением детали.

На рис. 3.1 представлена схема нагружения круглого образца 1, установленного на двух вращающихся опорах 2. Силы P через подшипник 3 нагружают образец так, что на среднем участке (с меньшим диаметром) создаётся чистый изгиб. Эпюра изгибающих моментов показана на рис. 3.1, б. Максимальные напряжения на этом участке определяются по формуле:

σ_max = = (3.1)

где d – диаметр образца на среднем участке.

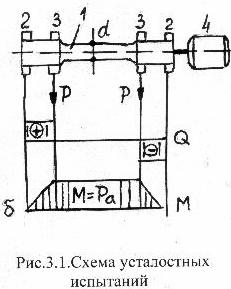
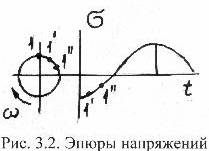
При помощи электродвигателя 4 образец 1 вращается со скоростью ω, при этом наружные кольца подшипников 3 остаются неподвижными, а следовательно, не изменяется направление действия силы P, в связи с этим в точке 1 поперечного сечения образца нормальные напряжения будут меняться циклически, как показано на рис. 3.2. Как видим, при такой схеме нагружения создаётся симметричный цикл изменения напряжений с параметрами:

σ_m = 0; σ_a = ±; R = -1; T = 2π / ω

При изменении P будет соответственно изменяться амплитуда цикла. При испытании партий образцов (по 5 – 6 штук) создают такие нагрузки, чтобы образцы разрушились, выдержав определённые числа циклов нагружения N_p, которые определяются по формуле N_p = t_p, где t_p- время испытания образца. Порядок задания ступеней нагружения для каждой партии образцов в большинстве случаев принимают ниспадающим, т.е. на первую партию дают нагрузки, при которых σ_a = σ_max несколько ниже предела: прочности, нагрузки на последующие партии постепенно снижают. Число оборотов в минуту n = 30ω/π наиболее распространённых машин для испытания на усталость обычно не превышает 3000 об/мин, поэтому испытание на усталость каждого образца иногда требует продолжительного времени, исчисляемого неделями непрерывной работы машины.

Обработка результатов усталостных испытаний заключается в построении кривой усталости (выносливости), или кривой Веллера. Кривую усталости строят по точкам в координатах число циклов N – напряжения σ_max = σ_a. Каждому разрушившемуся образцу на диаграмме соответствует одна точка с координатами N_pi и σ_ai (рис. 3.3).

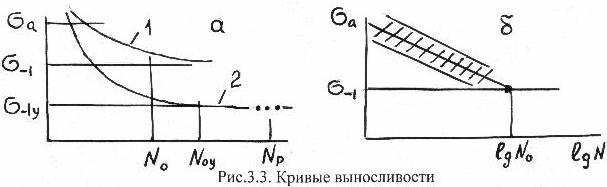
Как правило, кривые выносливости стальных образцов при высоком уровне напряжений резко падают вниз (кривая 1, рис. 3.3, а), а по мере их снижения асимптотически приближаются к горизонтальной прямой, отсекающей на оси координат амплитуду напряжений σ_-1, которая носит название “предел выносливости”. В общем случае под пределом выносливости (σ₁, σ_R) будем понимать амплитуду симметричного цикла (или максимальное напряжение несимметричного цикла), при которой и ниже которой не происходит усталостных разрушений образца при неограниченном числе циклов нагружения. Ордината точки на кривой 1, где кривая практически совпадает с асимптотой, т.е. соответствует напряжению, при котором образец не разрушится, носит название “база испытаний N_o”. Для чёрных металлов (сталь, чугун) база испытаний соответствует 10⁷ циклов. Кривые выносливости цветных металлов (медь, алюминий) по существу не имеют асимптот (рис. 3.3, а, кривая 2), поэтому база испытаний здесь принимается условно и соответствует (5-10) • 10⁶ циклов. Поэтому и предел выносливости цветных металлов σ_-1Y является условным, равным амплитуде напряжений соответствующей (принятой) базе испытаний. По кривым выносливости, построенных в координатах N-σ_a трудно определить Nо₄ σ_-1 поэтому на практике построение кривых выносливости производится в координатах σ_a-lgN, как показано на рис. 3.3,б (график 1). Из графика 1 определяются следующие характеристики сопротивления усталости образца:

- σ. (σ₂) – предел выносливости;

- No - база испытаний;

- m = ctgd - показатель наклона левой ветви. Уравнение левой ветви кривой выносливости в координатах σ_a-lgN имеет вид:

σ ^b_-1N_o = σ ^m_aiNi (3.2)

На основании многочисленных экспериментов для некоторых материалов установлены соотношения между пределами выносливости при различных видах деформаций: изгибе (σ ^u_-1), кручении (τ_-1), растяжении (σ ^о₁), Для гладких образцов эти соотношения имеют вид:

τ_-1 = 0,8 σ ^u_-1; σ ^о_-1 = 0,65 σ ^u_-1 - для чугуна (3.3)

На практике также используются полученные опытным путем зависимости между пределом прочности σ_в при растяжении материала и пределом выносливости образца при различных видах деформаций:

σ ^о_-1 = 0,28σ_в; σ^о_-1 = 0,4σ_в; τ_-1 = 0,22σ_в (3.4)

Кривые выносливости 1,2 на рис. 3,3,а и кривая 1 на рис. 3.3,б построены по средним значениям N_p партии образцов, испытанных на каждом уровне нагружения. На рис. 3.3,6 показано поле рассеивания (заштрихованная область) экспериментальных данных. С учетом этого обстоятельства характеристики сопротивления усталости σ _-1, N_o, m: можно считать случайными величинами, имеющими средние значения σ _-1, Ň_о, m и средние квадратические отклонения от них. Поэтому в литературе /4,5,6/ приводятся средние значения предела выносливости σ и коэффициент вариации предела выносливости V_o = S_σ-1/σ _-1 где S_σ-1 - среднее квадратическое отклонение предела выносливости. На величину предела выносливости влияют характеристики циклов напряжений, форма и размеры испытываемого образца, состояние его поверхности, среда, в которой производятся испытанию температура, режим циклического воздействия (тренировка образца, паузы в проведении испытаний, перегрузки, частота напряжения), внутренние сварочные и другие напряжения. Для выяснения влияния того или иного фактора а качестве эталона принят предел выносливости σ_- , полученный при испытании образцов на воздухе при симметричном цикле для партии гладких полированных образцов диаметром 7-10 мм. Влияние различных факторов оценивается отклонением характеристик сопротивления усталости эталонных образцов от рассматриваемых. Основными факторами, влияющими на предел выносливости являются следующие:

- Концентрация напряжений в детали, оценивается эффективным коэффициентом:

K_σ = σ_-1/ σ _-1H (3.5)

где σ _-1H - предел выносливости образца с искусственно созданным концентратором.

- Шероховатость поверхности, оцениваемая коэффициентом

K_F = σ _-1H / σ_-1 (3.6)

где σ _-1H - предел выносливости образца с заданной шероховатостью поверхности.

- Абсолютные размеры образца, оцениваемые коэффициентом

Kd = σ _-1d / σ_-1 (3.7)

где σ _-1d – предел выносливости образца заданного диаметра.

С учетом этих факторов предел выносливости рассчитываемой детали можно представить так:

σ _-1д = σ_-1 / K, где k = K_σ / K_FK_d, (3.8)

Вопросы выбора коэффициентов K_σ, K_F и K_d достаточно полно изложены в литературе / 1,2,3,7 /. Описанным выше способом можно оценить влияние различных факторов на предел выносливости деталей типа вал или ось. Для крупногабаритных литых и сварных деталей определить предел выносливости по результатам испытаний образцов практически не представляется возможным. Для таких деталей производятся натурные усталостные испытания на специальных стендах с гидравлическим нагружением / 4 /. Результаты натурных усталостных испытаний таких деталей показали, что у литых корпусных деталей автомобилей, тракторов и сельхозмашин, выполненных из ковкого чугуна различных марок предел выносливости, изменяется несущественно и колеблется в пределах σ _-1 = 48-50 МПа.. Предел выносливости крупногабаритных стильных сварных (штампосварных) рамных конструкций различных транспортных машин зависит в большей степени от их конфигурации и качества сварных соединений, а не применяемого материала и изменяются в диапазоне σ _-1 = 55-70 МПа. Большие значения предела выносливости соответствуют конструкциям, у которых нет сварных швов в зоне появления трещин усталости.При расположении сварного шва в зоне высоких рабочих напряжений сопротивление усталости конструкции снижается на 30 %. Подрезы, поры и прогары при сварке приводят к снижению предела выносливости сварных конструкций вдвое. Усталостную прочность сварных конструкций можно повысить созданием деконцентраторов: сверлением отверстий в местах пересечений и в конце сварных швов.

< В начало >

< Содержание >