|

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ЦЕНТР ДИСТАНЦИОННОГО ОБУЧЕНИЯ
Кафедра «Сервис и техническая эксплуатация автотранспортных средств»
Конструкция, расчет и потребительские свойства автомобилей
ЭКСПЛУАТАЦИОННЫЕ СВОЙСТВА АВТОМОБИЛЯ
ТЕОРИЯ И РАСЧЕТ
Учебное пособие
3.1. Продольная устойчивость автомобиля
Продольная устойчивость автомобиля характеризуется возможностью его опрокидывания вокруг передней или задней оси.
Рассмотрим общий случай движения автомобиля – ускоренное движение на подъеме с прицепом (рис. 16).
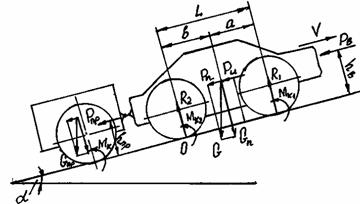
Рис. 16. Схема сил при движении автомобиля на подъем
Уравнение моментов сил относительно точки О – возможной точки опрокидывания, имеет вид:
R1L+Pвhв+Pnh+Puh-Gnb+Pпрhпр+Mk1+Mk2+Mk=0
Приравняв нулю нормальную реакцию R1 на передние колеса, получим выражение, определяющее предельное по устойчивости
состояние автомобиля:
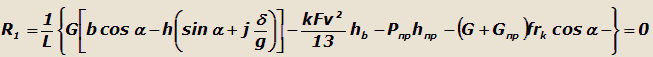 |
(18) |
где формулы для сил Рв, Рn, Ри, Gn и моментов МК1, МК2, МК взяты из
уравнения 11 для определения нормальной реакции R2. Принято, что радиусы rк колес автомобиля и прицепа равны.
Опрокидывание автомобиля через заднюю ось может произойти при преодолении максимального подъема из-за действия
составляющей силы веса Рn, силы инерции Ри и при движении с максимальной скоростью из-за силы сопротивления воздуха Рв.
При движении автомобиля на максимальный подъем его скорость бывает мала и поэтому можно пренебречь силой сопротивления
воздуха Рв. Можно принять также, что преодоление подъема происходит с установившейся скоростью (j=0), так как разгон на максимально допустимом подъеме невозможен.
При этих условиях получим:
Gbcosα-Ghsinα-Pпрhпр-(G+Gпр)frkcosα=0.
Принимая Pпр=Gпрsinα, получим:
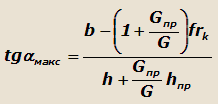 |
(19) |
Выражение (19) позволяет определить максимальную величину подъема, которую автомобиль с прицепом может преодолеть
при установившейся скорости движения без опрокидывания.
При движении по хорошей дороге (f≈0), без прицепа (Рпр=0) величина подъема увеличится и станет равной:
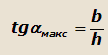
Опрокидывание автомобилей обычных конструкций вокруг передней оси практически невозможно,так как расстояние b≥a,
а для легковых автомобилей – величина h мала.
Автомобили по своим тяговым качествам или по сцеплению колес с дорогой не всегда могут въехать на предельный по
опрокидыванию подъем. Поэтому при проектировании автомобиля необходимо установить, чем ограничивается максимальный
угол подъема – опрокидыванием, буксованием или недостатком тяговой силы.
Весьма актуальным является анализ этого свойства для автомобилей повышенной проходимости, которые способны
преодолевать большие подъемы и имеют высокое расположение центра масс. Для этих автомобилей ведущими являются
все колеса и поэтому максимально допустимая по условиям сцепления с дорогой тяговая сила будет равна:
Pт. макс.=(R1+R2)φ=φGcosα=Pп=Gsinα,
tgαбукс=φ
Для того, чтобы буксование автомобиля со всеми ведущими колесами началось до его опрокидывания,
необходимо соблюдение следующего неравенства:
| tgαбукс.<tgαопр. или |
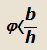 |
Большинство автомобилей проектируется так, чтобы максимальный подъем ограничивался буксованием ведущих колес,
а не опрокидыванием. Однако часто для автомобилей повышенной проходимости, у которых высоко расположен центр масс,
а шины с грунтозацепами обеспечивают большие значения коэффициента сцепления, предельные углы по буксованию и опрокидыванию очень близки.
|
