|

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ЦЕНТР ДИСТАНЦИОННОГО ОБУЧЕНИЯ
Кафедра «Сервис и техническая эксплуатация автотранспортных средств»
Конструкция, расчет и потребительские свойства автомобилей
ЭКСПЛУАТАЦИОННЫЕ СВОЙСТВА АВТОМОБИЛЯ
ТЕОРИЯ И РАСЧЕТ
Учебное пособие
3.2. Поперечная устойчивость автомобиля
Поперечная устойчивость автомобиля характеризуется его способностью двигаться без опрокидывания и скольжения
при прямолинейном движении по дороге с поперечным уклоном и при движении на повороте.
При прямолинейном движении автомобиля по дороге с поперечным уклоном опрокидывающая сила равна составляющей силы
веса G·sinb(рис. 17).
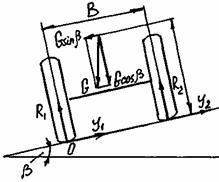
Рис. 17. Схема сил при движении автомобиля по дороге с поперечным уклоном
Из условия равновесия автомобиля относительно оси проходящей через точки О опоры левых колес, получим:
R2B+Ghsinβ-G(b/2)cosβ=0
где R2 - сумма нормальных реакций на правых колесах;
В - колеса автомобиля.
В момент начала опрокидывания нормальные реакции на правые колеса автомобиля становятся равными нулю (R2=0), тогда:
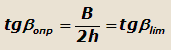 |
(20) |
До опрокидывания может начаться скольжение автомобиля под уклон. Если допустить, что колеса передней и задней осей
автомобиля имеют одинаковое сцепление с дорогой и что боковые реакции y1 и y2 распределяются по осям так же, как и составляющие
силы веса, то получим:
y1+y2=Gsinβ=φGcosβ
или
tgβскол.=φ
При условии, когда j<В/2h, скольжение колес автомобиля начинается раньше его опрокидывания.
При движении автомобиля на повороте по горизонтальной дороге опрокидывающей является центробежная сила
Рц (рис. 18) равная:
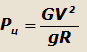
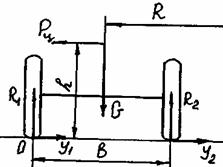
Рис.18. Схема сил при движении автомобиля на повороте
Опрокидывание автомобиля начнётся в тот момент, когда нормальная реакция R2, действующая на внутренние колёса,
будет равна нулю. Из условия равновесия автомобиля относительно оси, проходящей через точки О опоры внешних колёс, получим:
R2b+Pц-G·b/2=0
Приравнивая реакцию R2 к нулю и подставляя значение центробежной силы, получим:
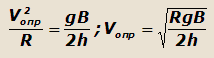 |
(21) |
Боковое скольжение автомобиля начнется в тот момент, когда сумма боковых реакций достигнет силы сцепления φ G, т.е. при:
(Y1+Y2)макс.=Pц. макс.=G/g·V2/R=φG
или
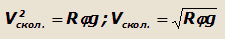 |
(22) |
При движении автомобиля на его поперечную устойчивость оказывает существенное влияние поперечный профиль дороги
на закруглениях, т.е. на виражах. Рассмотрим условия поперечной устойчивости автомобиля при движении на вираже.
Опрокидывающей силой в этом случае будет составляющая Рцcosβ центробежной силы (рис. 19). Составляя уравнение моментов
сил по отношению к оси, проходящей через точки О опоры верхних колес, получим:
-R1B+Ghsinβ+Pц(B/2)sinβ-Pцhcosβ+G(B/2)cosβ
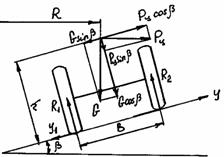
Рис.19. Схема сил при движении автомобиля на вираже
Подставляя в это уравнение выражение для центробежной силы и приравнивая реакцию R1 нулю, получим:
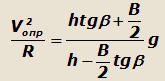
Разделим числитель и знаменатель правой части полученного выражения на h и заменяя
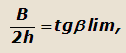 |
запишем окончательно |
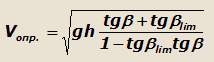 |
(23) |
Из уравнения (23) видно, что если выбирать соответствующие углы β, то скорость движения может быть произвольно велика и,
если
1-tgβlimtgβ=0
или
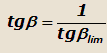
то опрокидывания не произойдет при любой сколь угодно большой скорости.
Автомобиль начнет скользить вбок при условии:
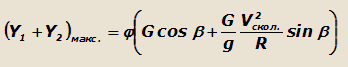
Из условия равновесия автомобиля относительно оси у (рис.19) запишем:
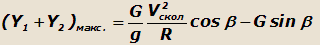
Решая эти уравнения совместно, получим:
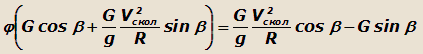
или
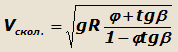 |
(24) |
Сравнивая значения Vопр. и Vскол., рассчитанные по формулам (23) и (24), можно определить, что наступит раньше,
опрокидывание или скольжение автомобиля вбок.
Уравнение (24) позволяет установить, что при увеличении угла β скорость движения автомобиля, допустимая по скольжению вбок, также увеличивается, и что
при 1-φtgβ=0 эта скорость может быть равна бесконечности. Таким образом, при tgβ=1/φ скольжения вбок не будет, и скорость движения может быть произвольно велика.
Чтобы увеличить поперечную устойчивость автомобиля при высоких скоростях движения в реальных дорожных условиях,
закругления на автомагистралях выполняют с большими радиусами, порядка 300…1000 м, а полотну дороги придают на закруглениях
поперечный уклон, направленный к центру закругления; величина уклона берется в пределах β=8…120°.
При рассмотрении процесса поперечного скольжения автомобиля было принято допущение, что боковое скольжение начиналось
одновременно как для передних, так и для задних осей. В общем случае скольжение передних и задних колес может начаться
неодновременною или происходить с неодинаковой интенсивностью, в результате чего возникает непроизвольный поворот машины вокруг какой – то вертикальной оси.
Такое явление называется заносом. Заносы чаще всего наблюдаются при резких торможениях и разгонах, на поворотах, при движении по дороге с поперечным уклоном и т.д.
Влияние перечисленных факторов особенно проявляется на мокрых и скользких дорогах и в других случаях, когда сцепление колес с дорогой ухудшается.
Возможность заноса при торможении и разгоне автомобиля объясняется тем, что в это время на колеса действуют значительные
касательные силы, а их наличие снижает устойчивость колес против бокового скольжения. При разгоне автомобиля ведущая ось
более подвержена боковому скольжению, так как через ее колеса передается крутящий момент.При торможении автомобиля боковое скольжение может начинаться в
равной мере, как для ведущей оси, так и для ведомой.
На рис. 20 показана схема автомобильного колеса, нагруженного вертикальной Gк и боковой Рб силами, а также
моментом mк
вызывающая тяговую силу Рт.
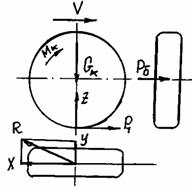
Рис.20. Схема сил, действующих на автомобильное колесо
В площади контакта колеса с дорогой возникает реакция дороги от приложенных сил: от боковой силы – У,
от силы веса автомобиля, приходящейся на колесо – Z и от тяговой силы - Х.
Равнодействующая R окружной и боковой реакции (Х и У) расположена в плоскости дороги. Для того, чтобы колесо
не скользило, необходимо, чтобы сила сцепления колеса с дорогой была больше равнодействующей, т.е. R≤φZ.
Это условие позволяет определить максимальную допустимую по условию скольжения величину боковой реакции У:
X2+Y2=R2≤φ2Z2;
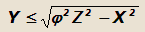
Из неравенства видно, что устойчивость колеса в значительной степени зависит от величины тяговой (или тормозной)
силы и в том случае, когда она достигнет своего максимального значения, равного φZ(X=φZ), теоретически достаточно любой,
как угодно малой боковой силы для того чтобы вызвать скольжение колеса вбок.
Рассмотрим условия бокового скольжения ведущей оси автомобиля, который совершает поворот по дуге окружности
с радиусом R, движется с постоянной скоростью и развивает на ведущих колёсах тяговую силу РТ.
На ось (рис. 21) приходится часть G1 полной силы веса G автомобиля и часть РЦ1 полной центробежной силы Рц,
действующей на автомобиль. В результате действия этих сил в точках опоры колес с дорогой возникают реакции: от тяговой силы – X'1 и X”1,
от боковой силы – Y'1 и Y”1, и вертикальной силы – Z'1 и Z”1.
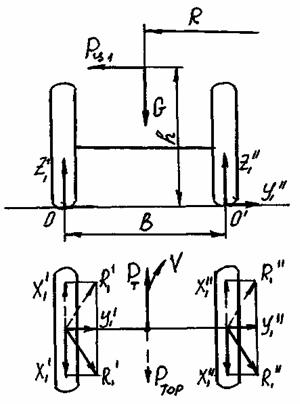
Рис.21. Схема сил, действующих на ось автомобиля
Внутренние и внешние колеса оси по разному нагружаются силами. Из-за центробежной силы перераспределяются по колесам
нормальные реакции, а из-за дифференциала -реакции тяговых сил.Из условия равенства моментов всех сил относительно оси,
проходящей через точку О опоры внешнего колеса имеем:
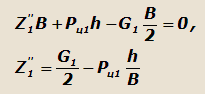
Аналогично, из условия равенства моментов относительно оси, проходящей через точку О, получим:
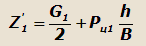
Как видно, нормальная реакция Z''1, действующая на внутреннее колесо, меньше нормальной реакции Z'1,действующей на внешнее
колесо.
Наличие дифференциала обеспечивает передачу большей части крутящего момента через отстающее, в данном случае,
внутреннее колесо. Поэтому при всех условиях X'1<X”1.
Таким образом, внутреннее колесо (на рис. 21 – правое) нагружено меньшей нормальной реакцией и большей реакцией
от тяговой силы. Следовательно, внутреннее колесо ведущей оси автомобиля раньше, чем внешнее, теряет устойчивость и начинает буксовать.
В момент начала буксования одного колеса почти вся суммарная боковая сила начинает восприниматься другим колесом,
нагруженным еще и тяговой силой. Часто оно оказывается не в состоянии передать суммарную боковую силу, что приводит к заносу всей оси.
Поперечное скольжение вбок задней или передней оси по-разному влияет на устойчивость автомобиля.
При заносе задней оси направление ее движения не совпадает с продольной осью автомобиля и определяется
вектором VB (рис. 22, а). Передняя ось продолжает движение в неизменном направлении, определяемом вектором VA.
Эти два вектора позволяют определить положение мгновенного центра поворота путем восстановления перпендикуляров
к этим векторам. В результате движения автомобиля вокруг центра О возникает центробежная сила Рц, которая ориентирована в
сторону заноса задней оси и таким образом стремится его увеличить.
При заносе передней оси автомобиля (рис. 22,б) мгновенный центр поворота лежит на продолжении задней оси.
Движение автомобиля вокруг этого мгновенного центра также приводит к возникновению центробежной силы Рц,
но она в отличие от первого случая будет направлена в сторону, противоположную направлению начинающегося заноса. В результате центробежная
сила будет препятствовать заносу, и автомобиль в поперечном направлении будет устойчивей.
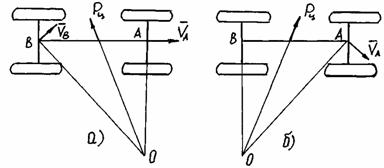
Рис.22. Схема сил при заносе задней оси (а) и передней оси (б)
Из вышеприведенных рассуждений следует, что необходимо в первую очередь рассматривать устойчивость против
бокового скольжения задней оси автомобиля, если ось ведущая и в любом случае при торможении автомобиля.
Для установления зависимости, определяющей условие устойчивости по буксованию колес задней ведущей оси,
вернемся к ранее полученному соотношению между реакцией от тяговой силы и нормальной реакцией дороги на внутреннем колесе при его скольжении:
X1"=φ·Z1",
где X”1 - реакция от составляющей тяговой силы на внутреннем колесе автомобиля при повороте (см. схему на рис. 21);
Z”1 - нормальная реакция дороги.
Полагая, что дифференциал незначительно влияет на перераспределение тяговых сил по полуосям, запишем, что
X1"=0,5·PT
Учитывая ранее выведенную зависимость для нормальной реакции:
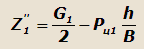 |
и подставляя значение Z”1 в выражение для реакций X”1 , получим: |
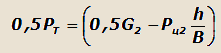 |
(25) |
где G2 - сила веса автомобиля, приходящихся на заднюю ось;
РЦ2 - часть центробежной силы, приходящаяся на заднюю ось.
Для введения в уравнение параметров движения V и R заменим величины тяговой и центробежной сил их значениями.
Тяговая сила PТ, необходимая для движения с постоянной скоростью по горизонтальной дороге, равна:
PT=f·G+k·F·V2
Центробежная сила, действующая в центре масс автомобиля, равна:
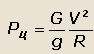
Часто центробежной силы автомобиля, приходящейся на заднюю ось, равна:
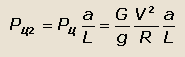
где а – расстояние от центра масс до передней оси автомобиля.
Подставляя значение тяговой и центробежной сил с выведенное уравнение, получим:
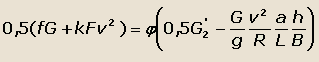
тогда скорость автомобиля определится по формуле:
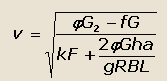 |
(26) |
Выведенная зависимость определяет соотношение между основными параметрами установившегося движения на повороте
(v и R) при начинающемся заносе ведущей задней оси и показывает, какие факторы влияют на устойчивость автомобиля.
В случае торможения автомобиля, совершающего поворот на дуге окружности радиуса R и с постоянной скоростью v (схема действия реактивных
сил на колесах автомобиля показана на рис. 21 пунктиром), уравнение (25) можно записать в виде:
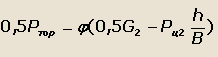
где Pтор - сила торможения, приходящаяся на заднюю ось.
Тогда скорость автомобиля определится по формуле:
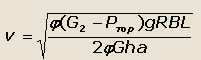 |
(27) |
Приведенный анализ относится к случаю движения автомобиля с постоянной скоростью на повороте постоянного радиуса.
В действительности движение автомобиля характеризуется переменными значениями этих параметров, а потеря устойчивости
автомобилем часто происходит именно при изменении скорости движения или радиуса поворота.
Рассмотрим схему движения автомобиля на повороте при переменных значениях скорости и радиуса. Траектория движения
автомобиля в этом случае имеет вид, показанный на рис. 23.
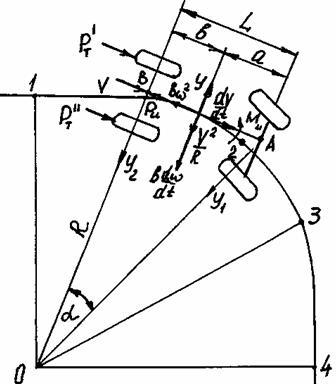
Рис. 23. Схема движения автомобиля на повороте
На участке 1-2 начинается поворот автомобиля с постепенным увеличением угла α поворота управляемых колес.
При этом автомобиль движется по кривой переменного радиуса R кривизны. Далее на участке 2-3 автомобиль движется при
постоянном положении управляемых колес. Радиус поворота автомобиля R=const.
На участке 3-4 автомобиль начинает выходить из поворота с постепенным уменьшением угла α поворота управляемых колес
и снова движется по кривой переменного радиуса. В точке 4 поворот полностью закончен и автомобиль начинает прямолинейное движение.
На схеме рис. 23 цифрами 1-4 обозначены положения точки В автомобиля.
Движение автомобиля в рассматриваемом случае можно представить состоящим из двух движений: из движения точки В
округ мгновенного центра поворота О и вращения автомобиля вокруг точки В.В результате движения точки В автомобиля вокруг
мгновенного центра возникают нормальное V2/R и касательное dV/dt ускорения, которые могут быть перенесены в центр масс автомобиля.
В результате вращения автомобиля вокруг точки В с переменной угловой скоростью ω и центре масс возникают нормальное b·ω2 и касательное dV/dt ускорения.
Суммарное ускорение центра масс автомобиля, направленное вдоль его оси, равно
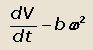
а направленное перпендикулярно продольной оси –
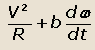
При движении центра масс автомобиля с ускорением возникают силы инерции:
| касательная сила инерции |
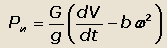 |
и нормальная боковая сила инерции |
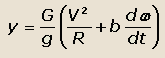 |
а также инерционный момент, который равен
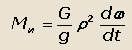
где ρ - радиус инерции автомобиля.
Определим величины боковых сил, действующих на переднюю и заднюю оси автомобиля, составляя уравнение
моментов сил относительно точки А – центра передней оси:
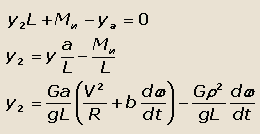 |
(28) |
Аналогично предыдущему из условий равновесия моментов по отношению к вертикальной оси, проходящей через точку В
– середину задней оси, получим:
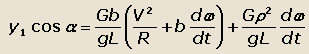
Известно, что
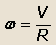
тогда
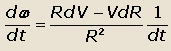
Из рис.23 следует, что
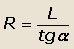
тогда
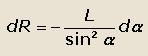
Подставляя полученное выражение для dR в уравнение для dw/dt, получаем:
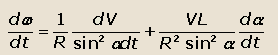
Подставляя выражение для dω/dt в уравнение для определения боковых сил y1 и y2, получим:
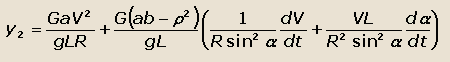 |
(29) |
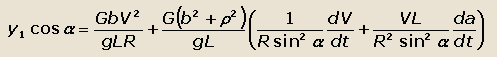 |
(30) |
Из уравнений (29) и (30) следует, что увеличение ускорения dV/dt автомобиля повышает боковые реакции y1 и y2, а
следовательно, понижает боковую устойчивость автомобиля при движении по первой переходной кривой, на рис. 23 – отрезок 1-2 траектории поворота.
Скорость поворота управляемых колес da/dt при движении по первой переходной кривой положительна и поэтому ее увеличение также приводит к
увеличению боковых реакций и к ухудшению боковой устойчивости автомобиля.
Аналогичный анализ, проведенный для второй переходной кривой, на рис. 23 – отрезок 3-4, показывает, что увеличение
ускорения автомобиля dV/dt и скорости поворота управляемых колес dα/dt уменьшает величины боковых реакций на колесах автомобиля, т.е. повышает его боковую
устойчивость.
Поэтому для сохранения боковой устойчивости автомобиля при быстром движении на повороте следует двигаться по первой
переходной кривой с замедлением и возможно медленнее поворачивать управляемые колеса, а по второй с ускорением и поворачивать управляемые
колеса возможно быстрее.
|
