1. ФУНКЦИОНАЛЬНЫЕ ПАРАМЕТРЫ ДЕТАЛЕЙ И АКТИВНЫЙ КОНТРОЛЬ РАЗМЕРОВ
1.1. Модель параметра детали как составляющая системы активного контроля
1.2. Функция и структура пары
1.3. Функция и структура детали
1.4. Функция и структура поверхности
1.5. Модель параметра
1.1. Модель параметра детали как составляющая системы активного контроля
Любая система автоматического контроля, используемая в процессе изготовления детали, может быть рассмотрена как некоторая система управления параметрами детали по результатам измерения этих параметров. В основу такой системы может быть положена схема, иллюстрирующая в общем виде задачу оптимизации параметров реальных объектов. Эта схема приведена на рис.1 с учетом составляющих технологической системы изготовления детали. На основе сравнения параметра х детали Д, формируемого в системе станок - приспособление - инструмент-деталь (СПИД), с его моделью М по заданному критерию сравнения r измерительное устройство И выдает некоторую количественную информацию в системе обратной связи (управления) У. При этом в качестве М может быть использована любая математическая модель (в простейшем случае фиксированные, например предельные, значения некоторого параметра, заданный размер детали, определенный уровень настройки и т.д.).
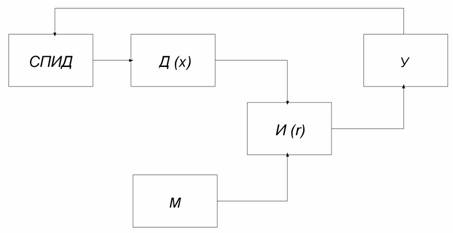
Рис. 1. Схема системы активного контроля детали
В любом случае модель параметра входит в качестве одной из важнейших составляющих в систему управления и должна быть исследована не только с точки зрения точности измерений, но и с позиций обоснования самого выбора контролируемого параметра. При этом выбор параметров деталей и обоснование их предельных значений, т.е. формирование моделей параметров, является одним из ключевых вопросов создания машин. С одной стороны, свойства детали и параметры, определяющие эти свойства количественно, обусловлены способностью детали выполнять свою функцию (назначение) и непосредственно связаны с эффективностью работы изделия в целом, т.е. с его качеством. Такие параметры могут быть рассмотрены как функциональные ( определяющие функционирование) и определены в соответствии со стандартной терминологией как показатели качества детали. С другой стороны, модель параметра определяет, наряду с измерительным устройством, достоверность информации, используемой при управлении технологической системой и влияет таким образом на эффективность процесса изготовления изделия.
Вопросы определения моделей параметров решают при проектировании детали, т.е. в процессе формирования ее модели. В этом случае термин «модель» условимся понимать в широком смысле как любой образ (мысленный или условный: изображение, описание, схема и т.п.) какого-либо объекта, процесса или явления, используемый в качестве его « заместителя», «представителя». В настоящее время традиционной формой модели детали является ее чертеж. Модель детали в форме чертежа не является совершенной и обладает рядом недостатков. Например: при выполнении чертежа относительно велик объем чисто оформительской работы; чертеж детали не содержит в явном виде указаний о ее базовых поверхностях. С точки зрения автоматизации проектирования чертеж не является оптимальной формой информации о детали, так как не может быть непосредственно введен в ЭВМ и требует перевода на язык программирования.
Процесс разработки чертежа детали (ее проектирование) не регламентирован строгими методиками (стандарты ЕСКД устанавливают лишь правила оформления чертежей), в результате чего в ряде случаев конструктор-деталировщик принимает интуитивные и неоднозначные решения, что приводит к неверному выбору и ограничению параметров деталей, т.е. к созданию неоптимальных конструкций и снижению качества изделий.
Отсутствие строгих алгоритмов процесса проектирования деталей затрудняет автоматизацию проектных работ на этапе конструирования деталей, а неоптимальные модели деталей снижают эффективность технологического проектирования (в частности - автоматизированного ) и процессов изготовления деталей (в том числе с использованием систем активного контроля). Поэтому задача упорядочения процесса формирования моделей деталей и их параметров с целью совершенствования этих моделей является актуальной как с точки зрения повышения качества изделий автоматизации проектирования, так и с позиций управления процессом изготовления деталей, в частности с позиций разработки систем активного контроля и средств измерений.
При анализе какого-либо объекта на основе системного подхода должны быть исследованы как основные признаки системы – его функция и структура. Поскольку всякая деталь является подсистемой некоторого механизма, представляется целесообразным рассматривать функцию и структуру детали, исходя из функций и структуры механизма в целом.
1.2. Функция и структура пары
На основе представления о кинематических парах, соединениях деталей машин и базах становится возможным рассмотрение некоторой обобщенной модели пары. Для этого проанализируем в общем виде взаимодействие двух деталей, составляющих часть некоторого механизма (рис.2). Функция положение рассматриваемого элемента механизма может быть охарактеризована параметром A∆(1-2), замыкающим функциональную цепь, образованную параметрами А1; A(1-2), A2 связывающими некоторые ( в общем случае – произвольные) точки поверхностей деталей А1 – разных поверхностей детали 1, А2 –разных поверхностей детали 2.
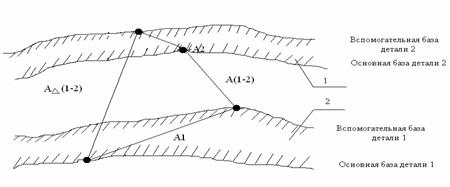
Рис. 2. Схема обобщенной модели пары
Таким образом, в функциональной цепи пары два звена являются параметрами связи поверхностей различных деталей. Параметр A∆(1-2) характеризует пару деталей как подсистему – часть функциональной цепи механизма и определяет в этой подсистеме связь вход - выход, т.е. функцию положения пары.
Величина A(1-2) является параметром связи пары поверхностей деталей, по которым происходит взаимодействие деталей 1 и 2 пары. Эти поверхности (в частных случаях - линии или точки) называют элементами пары. В дальнейшем условимся в пределах данной работы термином "пара" обозначать пару деталей, а во втором случае использовать термин "пара поверхностей".
Функциональная цепь пары 1 и 2 в общем случае является пространственной. При рассмотрении пары могут быть использованы проекции функциональной цепи на оси координат (рис. 3). При переходе к поверхностям правильной формы схема представлений упрощается. На рис. 4, а, б, в показаны примеры пар 1 и 2, образованных деталями с номинально цилиндрическими и плоскими поверхностями. Функциональную цепь пары деталей (см. рис, 2), состоящую из четырех звеньев, можно рассматривать как схему структуры пары.
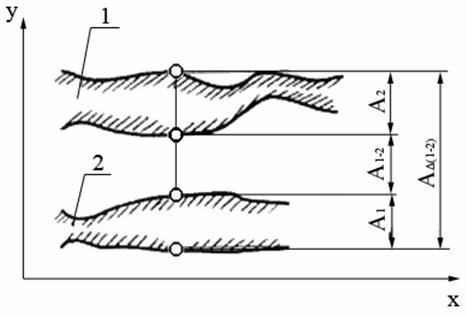
Рис. 3. Схема проекции функциональной цепи пары на ось У
На основе анализа множества пар различных механизмов, проведенного с точки зрения определения их функций, функцией пары можно считать осуществление и ограничение требуемых относительных движений (положений) деталей в паре, т.е. обеспечение ее функций положения A∆(1-2). Рассмотрим далее составляющие звенья функциональной цепи пары, в первую очередь параметр A(1-2). Пары поверхностей по значениям параметра A(1-2) можно разделить на три принципиальные группы.
В первом случае оба предельные значения параметра A(1-2) определены некоторыми положительными величинами, т.е. имеет место гарантированный зазор между поверхностями, их контактирование исключено. Такие пары поверхностей условимся называть бесконтактными.
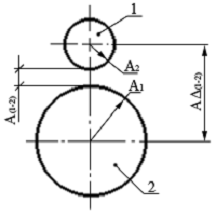 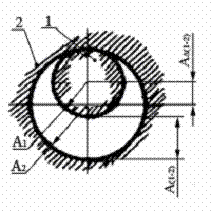 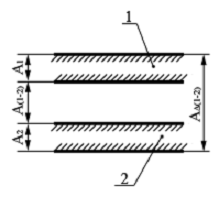
Рис. 4. Схема функциональных цепей деталей поверхностей правильной формы: а и б - цилиндрической формы; в - с плоскими поверхностями
Во втором случае поверхности соединены с натягом (предельные значения параметра A(1-2) в этом случае условимся считать отрицательными). При этом обеспечивается отрицательный аналог движения - сопротивление относительному смещению, т.е. относительная неподвижность деталей. Примерами таких пар поверхностей могут служить посадки с гарантированным натягом. В этих случаях натяги создают в процессе сборки изделий. При анализе их работы можно говорить о "предварительных" натягах. По своему влиянию на параметр пары A∆(1-2) натяги, осуществляемые по цилиндрическим и плоским поверхностям, различаются. Так, натяги по плоским поверхностям непосредственно влияют на замыкающее звено цепи и по величине могут быть соизмеримы с допусками звеньев размерной цепи. Для посадок цилиндрических поверхностей с натягом естественно предположить, что из-за неравномерности свойств материалов деталей, отклонений направления сил при запрессовке и ряду других причин возможно относительное смещение осей отверстия и вала. Очевидно, однако, что смещения эти должны быть несоизмеримо меньшими, чем при зазорах, и не определяются детерминировано величиной натяга.
В третьем случае наибольшие и наименьшие предельные значения параметра пары поверхностей определены условием 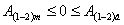 . Принимая в первом приближении (без учета сложного характера контактирования реальных поверхностей), что при А(1-2) = 0 имеет место контактирование поверхностей, можно определять этот случай, как промежуточный по отношению к первым двум, т.е. как общий случай взаимодействия поверхностей. По направлению и параметрам требуемого относительного движения поверхностей (с учетом действующих сил) на основе исследований, посвященных трению и износу в машинах, могут быть определены характер контактирования и свойства поверхностей деталей (допуски формы, параметры шероховатости, свойства поверхностного слоя материала и т.д.). . Принимая в первом приближении (без учета сложного характера контактирования реальных поверхностей), что при А(1-2) = 0 имеет место контактирование поверхностей, можно определять этот случай, как промежуточный по отношению к первым двум, т.е. как общий случай взаимодействия поверхностей. По направлению и параметрам требуемого относительного движения поверхностей (с учетом действующих сил) на основе исследований, посвященных трению и износу в машинах, могут быть определены характер контактирования и свойства поверхностей деталей (допуски формы, параметры шероховатости, свойства поверхностного слоя материала и т.д.).
Пары, работающие с контактированием и натягом, могут быть определены как пары передачи движения и базирования.
1.3. Функция и структура детали
Функция детали как звена механизма определена функцией целого механизма и может быть сформулирована как обеспечение необходимых относительных положений поверхностей. В свою очередь, функция детали определяет функции ее поверхностей. На основе классификации пар и представлений о базах поверхности деталей по их функциям могут быть разделены на базовые (основные и вспомогательные) и бесконтактные. Основными базами являются поверхности детали, которые определяют ее положение в машине; вспомогательными - поверхности, с помощью которых она определяет положение других деталей (ГОСТ 21495-76).
Практика простановки размеров в чертежах деталей показывает, что относительное положение поверхностей одной и той же детали может быть задано различным образом, т.е. допускается множество вариантов поверхностей, т.е. множество структур одной детали.
Естественно предположить, что среди множества формальных структур должен существовать один принципиальный вариант структуры, соответствующий оптимальной схеме функционирования детали и оптимальному процессу ее формирования при изготовлении. Такое положение согласуется с утверждением о том, что для каждой детали возможен лишь один вариант простановки размеров, соответствующий служебному назначению (функции детали) и определяющий наибольшие значения допусков размеров. Такой функциональный вариант простановки размеров детали выявляют из анализа размерных цепей изделия. Рассмотрим структуры двух типовых деталей машин - вала и стакана. Системы связей поверхностей этих деталей показаны на рис 5,а,б.
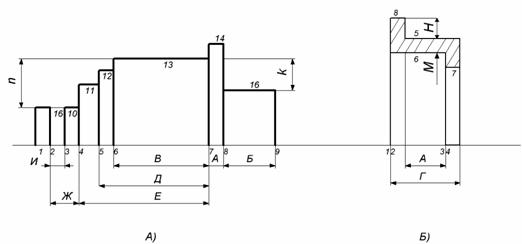
Рис. 5. Схема функциональной детали простановки размеров:
а – вала; б – стакана
Сформированная таким образом система параметров связи поверхностей детали может быть отражена графом структуры детали (рис. 6, 7). Вершинами графа обозначены поверхности детали, ребрами - их связи. Каждая из поверхностей деталей должна быть определена рядом параметров, отражающих свойства поверхностей. К параметрам связей, в соответствии со сложившимися представлениями могут быть отнесены размеры, определяющие относительное положение поверхностей детали (координирующие) и отклонения (допуски) расположения поверхностей. Система связей поверхностей может быть исследована с помощью ее проекций на оси координат. На рис. 6 и 7 показаны связи плоских поверхностей, совпадающие по направлению с осью X, и связи цилиндрических поверхностей, одинаково проецируемые на оси У и Z. Граф может быть построен с разделением поверхностей деталей в зависимости от их функций на три уровня (см. рис. 6 и 7).
Рис. 6. Граф структуры вала: поверхность 7 – основная база связей поверхностей по оси Х; поверхность 13 – основная база связей поверхностей по осям Y и Z
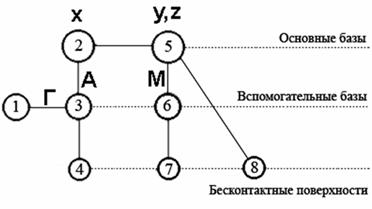
Рис. 7. Граф структуры стакана: поверхность 2-основная база связей поверхностей по оси X; поверхность 5 - основная база связей поверхностей по осям У и Z
Кроме указанных, на деталях в ряде случаев формируют поверхности в чисто технологических целях (центровые отверстия, фаски, канавки для выхода инструмента и т.д.).
После выявления системы параметров деталей необходимо провести их нормирование, т.е. определение их предельных значений. В настоящее время при нормировании параметров широко применяют метод аналогии с работающими конструкциями, явно недостаточный с точки зрения оптимального проектирования. Поэтому всякое совершенствование методов обоснования предельных значений параметров деталей представляется актуальным. На основе разделения поверхностей по уровням графа процесс нормирования параметров деталей может быть несколько упорядочен. Так, для бесконтактных поверхностей (третий уровень графа) собственные свойства поверхностей практически ограничиваются требованиями коррозионной стойкости, чистоты (отсутствия окалины, ржавчины и т.д.) и эстетики. Параметры связи бесконтактных поверхностей с базовыми могут быть ограничены допусками последних квалитетов (с проведением поверочного расчета соответствующих размерных цепей). Более сложную задачу представляет нормирование свойств и связей базовых поверхностей. Для решения такой задачи представляется целесообразным дальнейшее исследование и классификация пар функциональных цепей с учетом кинематических и динамических моделей цепей.
Разработанная модель детали в виде многоуровнего графа отличается от существующих (в том числе используемых для автоматизированного проектирования технологических процессов) большей степенью организации, так как имеет единую структуру; органично связана с процессом проектирования деталей, тогда как большинство существующих описаний выполняются на основе готового чертежа без анализа его качества; содержит большую, чем чертеж детали, информацию, гак как в явном виде указывает базы детали; не требует выполнения чертежных работ, так как может быть выполнена "от руки".
1.4. Функция и структура поверхности
Функции пар и деталей определяют функции поверхностей, их форму и свойства. Для анализа структуры поверхности воспользуемся, в соответствии с правилами унификации, типовой (комплексной) поверхностью, которая должна представлять собой композицию большинства практических вариантов. В качестве одного из профилей такой поверхности предложено рассмотреть профиль поверхности не круглого зубчатого колеса (зубчатого кулачка) (рис. 8). Такой профиль является одним из наиболее сложных случаев и может быть представлен как комплексный профиль поверхности (синтезированная поверхность).
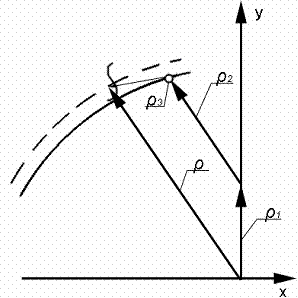
Рис. 8. Схема структуры комплексного профиля поверхности
Рассмотрим следующую схему теоретического формирования профиля реальной поверхности. Определяем:
- постоянную составляющую формы профиля, которая характеризуется радиусом 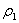 ; ;
- монотонно меняющуюся составляющую формы профиля, характеризуемую параметром 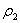 ; ;
- немонотонные формы (профили лысок, пазов, шпиц, зубьев и т. д.), положение которых можно охарактеризовать параметром ρ3 радиального и (или) тангенциального направления;
- две (всегда последние) составляющие профиля - искажения на уровне отклонений от формы и немонотонных форм, относимых к микронеровностям. Параметры отклонений формы и шероховатости регламентированы стандартами. В общем случае все эти параметры (ρ и ρ i) являются векторными, т.е. двухкомпонентными величинами.
Таким образом, каждый элемент реальной поверхности детали можно определить некоторым параметром ρ этой поверхности, который формируется цепью составляющих параметров, характеризующих структуру поверхности. Структурную цепь поверхности в некоторый момент времени можно определить на основании представлений об эквивалентных (заменяющих) механизмах схемой плоского четырехзвездника, если центры его шарниров поместить в центры кривизны профилей/ Параметр ρ имеет смысл функции положения такого механизма. Такую модель профиля поверхности легко можно трансформировать в более простые: при ρ3 = 0 - в монотонный профиль сложного характера, например, в профиль дискового кулачка; ρ2 = 0 - в профиль цилиндра вращения с вторичными формами в виде зубьев эвольвентного и неэвольвентного профиля, шлиц конфигурации и т.д.; ρ2 = ρ3 = 0 - в профиль цилиндра вращения; ρ1 = 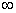 , ρ2 = 0 - профиль зубчатой рейки, резьбы (в осевом сечении) и т.д.; ρ1 = , ρ2 = 0 - профиль зубчатой рейки, резьбы (в осевом сечении) и т.д.; ρ1 = 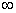 , ρ2 = ρ3 = 0 - в горизонтальную прямую линию; ρ1 = , ρ2 = ρ3 = 0 - в горизонтальную прямую линию; ρ1 = 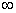 , ρ3 = 0 - в наклонную прямую линию и т.д. , ρ3 = 0 - в наклонную прямую линию и т.д.
Условимся различать:
- первичные формы поверхностей (профилей), определяемые монотонными структурными составляющими ρ1 и ρ2;
- вторичные, более мелкие, элементы формы - единичные, периодически повторяющиеся или расположённые случайным образом, в частности конструктивные элементы (пазы и т.д.), положение которых определяется параметром ρ3;
- элементы формы более высоких порядков.
Функциональный параметр ρ движущейся поверхности описывает некоторую воображаемую поверхность первичной формы, которая, хотя и не является материальной, в действительности определяет характер взаимодействия детали с парной деталью, комплексно учитывая мгновенные значения всех структурных составляющих.
Для сложнопрофильных пар представление о таких комплексных поверхностях не ново: воображаемые цилиндры, определяемые полоидными окружностями зубчатых колес и приведенными средними диаметрами резьбы, так же как производящие цилиндры резьбо- и зубообразующего инструмента, являются представлениями, давно освоенными практикой. Комплексные поверхности шлицевых деталей могут занимать некоторое промежуточное по профилю положение (для эвольвентных и треугольных шлиц) или совпадать с цилиндрами диаметров D и d. Положение о комплексной поверхности и структуре ее профилей дополняет сложившееся в практике представление о комплексных и дифференцированных погрешностях деталей.
При формировании поверхностей (генерации профилей) в процессе изготовления детали звенья структурной цепи поверхности должны быть материализованы соответствующими движениями элементов технологической системы. Это означает, что структура поверхности (профилей) определяет кинематику процесса формообразования деталей, хорошо согласуется с положениями кинематического анализа методов обработки деталей, определяет выбор оборудования и характер построения операций, в частности, согласование режимов главного движения и движения подачи. Кроме того структура поверхности и характер ее высокочастотных составляющих определяет выбор средств контроля, соответствующих детали по структуре и свойствам (например по дискретности, радиусу измерительного наконечника и т.д.).
Представление о структуре поверхности может быть принято за основу унификации поверхностей в машиностроении, а также унификации стандартов, регламентирующих допуски и посадки деталей различных сопряжений.
1.5. Модель параметра
Любой из параметров детали (параметр поверхности или связи поверхностей) в силу того, что в процессах изготовления и эксплуатации на него влияет большое число факторов (в том числе случайных), изменяется в пространстве и времени, т.е. является текущим. При этом следует отметить, что пространственные координаты точек поверхностей деталей связаны с координатой времени. Так, формообразование детали происходит в результате наложения движения в технологической системе, а отклонение пространственных характеристик деталей вызывает изменение параметров их движения. Поэтому вопросы точности деталей не могут быть решены в отрыве от исследования параметров их движения. При этом изменение некоторого параметра детали по пространственной и временной координатам могут быть описаны с точки зрения математики одинаково, т.е. на основе одной математической модели.
Процесс изменения параметра детали может быть отражен различными математическими моделями процессов, классификация которых рассмотрена в работе [22]. Поскольку познание реальных процессов происходит по схеме бесконечного ряда уточняющих представлений, для описания процессов используются модели различной степени неполноты, которые могут быть получены из бесконечного ряда его "усечением", "огрублением", схематизацией. Часть ряда, используемая в качестве модели, может быть представлена соответствующим математическим аппаратом. Остаток ряда определяет теоретическую погрешность модели, т.е. характеризует степень ее адекватности исследуемому явлению.
В качестве наиболее полной модели параметра детали может быть принята случайная функция, которая в предельных случаях может трансформироваться в случайную величину или аналитическую функцию. Модели параметров деталей в виде случайных функций и величин широко используются в практике управления технологическими процессами, в том числе - в системах активного контроля. В ряде случаев, в частности при описании поверхностей в задачах автоматизированного проектирования, возникает необходимость аппроксимации профилей поверхностей и траекторий движения профилей (или их точек) аналитическими функциями. Так разработаны многочисленные способы описания сложных поверхностей применительно к изделиям самолето-, судо-, автомобилестроения. На основе анализа существующих методов описания поверхностей предложена модель параметра поверхности в виде универсальной степенной функции, описывающей достаточно большой класс обводов и поверхностей.
Широко известен способ аппроксимации параметров деталей рядами Фурье. Предложено [14] описание поверхности детали в форме суперпозиции функций, аппроксимирующих профили этой поверхности. Таким же образом может быть описана некоторая воображаемая поверхность, получаемая при закономерном движении профиля. В качестве функции, аппроксимирующей профиль или траекторию движения, предложено использовать ряд Тейлора:
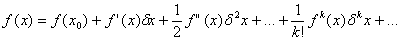
Представление параметра детали частной суммой ряда Тейлора позволяет использовать для анализа точности деталей один из самых универсальных инструментариев исследования функций в математике - аппарат производных. В соответствии с исходной схемой представлений анализ параметров деталей может быть проведен на разных уровнях: при полных и неполных моделях (стационарной, кинематической и динамической). При этом практически используются частные суммы из одного, двух или трех первых членов ряда, описывающих функцию, первую и вторую ее производные.
Метод исследования параметра с помощью производных является единым при анализе формы детали, изучении характеристик технологической системы и метрологических операций. Так, анализ формы деталей при помощи производных позволяет определить математически полные характеристики профиля в точке: крутизну профиля, экстремум, точки перегиба, величину, радиус, центр и окружность кривизны линии и др. Инструмент дифференцирования дает возможность положить в основу стандартизации элементов формы поверхностей единые, сквозные характеристики, позволяющие исчерпывающе описать неровности любого масштаба. Производные функции по времени, определяющие скорости и ускорения, т.е. параметры движения точки, могут быть рассмотрены как характеристики процессов формообразования детали в технологической системе и функционирования детали. При этом на основе производных могут быть найдены соответствующие аналогии пространственных и временных функций. Так, при помощи производных может быть определена неплавность работы соединений. В настоящее время плавность нормируется только для зубчатых колес. Очевидно, что понятие о плавности процессов сопряжения поверхностей является общим для многих видов сопряжений. Однако термин "плавность" не определяется в литературе однозначно. Можно предположить, что движение может считаться плавным, если функция этого движения монотонна в исследуемом интервале, т.е. не имеет точек перегиба. Это условие для функции f(x) соблюдается при постоянном знаке второй производной: f''(x) ≥ 0 или: f''(x) ≤ 0 в заданном интервале. Таким образом, плавность движения может быть однозначно определена с помощью производных условиями монотонности функции на участке и связана с соответствующими характеристиками монотонности профилей деталей. При этом представление параметра детали частной суммой ряда Тейлора структурно верно отражает смысл погрешностей системы СПИД по любой из координат, увязывает элементы формы деталей с движениями в технологической системе, дает возможность использовать отклонения формы деталей для диагностики положений, скоростей и ускорений в системе СПИД.
Поскольку производная К-го порядка есть математический инструмент исследования К - 1-й производной, следует предположить, что аппарат производных может рассматриваться как теоретическая модель системы многоступенчатого контроля параметров (включая и схему поверки средств измерения). При контроле деталей механическим способом (калибрами, штангенциркулями, микрометрами и т.д.) с линейными и плоскими измерительными наконечниками реализуется операция взятия экстремума функции на некотором интервале через нулевое значение первой производной, материализуемое измерительным наконечником.
Применение ряда Тейлора для описания параметра детали проиллюстрируем на примере описания номинально прямолинейного профиля поверхности. Прямой линией характеризуются следующие профили деталей: образующие цилиндрических и конических поверхностей (в том числе и профили продольных сечений зубьев зубчатых колес), рабочих поверхностей резьбы, шлицев и т.д. Отрезками прямых линий определяются также направляющие плоских поверхностей (например, призматических направляющих, направляющих типа "ласточкин хвост" и др.). Разлагая уравнение прямой линии в ряд Тейлора, в первом приближении получим
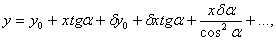 (1) (1)
где 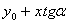 - нулевой член ряда, отображающий номинальное значение параметра и его структуру; у0 - соответствует постоянной составляющей р1; - нулевой член ряда, отображающий номинальное значение параметра и его структуру; у0 - соответствует постоянной составляющей р1; 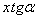 - монотонно меняющийся р2 (см. рис. 8). - монотонно меняющийся р2 (см. рис. 8).
Все последующие члены ряда составляют массив погрешностей параметра у, причем связи погрешностей обусловлены структурой номинального параметра. 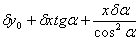 - первый член ряда, отображающий монотонно меняющуюся часть погрешности параметра у, причем слагаемое - первый член ряда, отображающий монотонно меняющуюся часть погрешности параметра у, причем слагаемое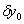 характеризует отклонение параметра у в момент начала процесса движения точки, определяется погрешностью относительной установки инструмента и заготовки при формообразовании поверхностей или детали и чувствительного элемента прибора в измерительной позиции. Эта погрешность участвует в дальнейшем развитии процесса как постоянная составляющая и соответствует понятию о начальных условиях процессов. Слагаемое характеризует отклонение параметра у в момент начала процесса движения точки, определяется погрешностью относительной установки инструмента и заготовки при формообразовании поверхностей или детали и чувствительного элемента прибора в измерительной позиции. Эта погрешность участвует в дальнейшем развитии процесса как постоянная составляющая и соответствует понятию о начальных условиях процессов. Слагаемое 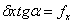 вызывает собой погрешность параметра у, вызываемую погрешностью аргумента вызывает собой погрешность параметра у, вызываемую погрешностью аргумента 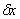 ; ; 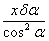 - погрешность параметра у, вызываемую отклонением угла α. Погрешности - погрешность параметра у, вызываемую отклонением угла α. Погрешности 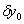 и и 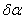 определяют соответственно точность расстояния и поворота профиля. определяют соответственно точность расстояния и поворота профиля.
Формула (1) в частных случаях приводит к известным представлениям. Так, когда прямая является образующей цилиндра, ось которого совпадает с осью х, величина 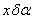 в соответствии со стандартной терминологией может быть обозначена как конусообразность, отклонение от параллельности образующей относительно оси детали или погрешность угла α = 0°. Для поверхностей резьб первый член ряда точно соответствует формуле погрешности, приведенного среднего диаметра резьбы. в соответствии со стандартной терминологией может быть обозначена как конусообразность, отклонение от параллельности образующей относительно оси детали или погрешность угла α = 0°. Для поверхностей резьб первый член ряда точно соответствует формуле погрешности, приведенного среднего диаметра резьбы.
Если уравнение прямой записано относительно х, первый член ряда Тейлора - 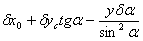 дает возможность оценки точности резьбы по осевой координате, а также полностью соответствует формуле погрешности базорасстояния конуса. Для торцов деталей слагаемое дает возможность оценки точности резьбы по осевой координате, а также полностью соответствует формуле погрешности базорасстояния конуса. Для торцов деталей слагаемое 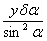 может быть рассмотрено как отклонение от перпендикулярности, торцовое биение и погрешность угла α=90°. может быть рассмотрено как отклонение от перпендикулярности, торцовое биение и погрешность угла α=90°.
Дальнейший анализ погрешностей профилей на основе разложения в ряд Тейлора позволяет классифицировать погрешности профилей по характеру их изменения, т.е. различать:
а) постоянную составляющую погрешности - погрешность в «момент начала движения точки вдоль профиля или во времени; представление о начальной точке профиля, ее координатах и ее погрешности соответствует понятиям о начальных условиях физических процессов;
б) монотонно меняющуюся на длине сопряжения составляющую погрешности; такая составляющая отражает представления об отклонении от параллельности и конусообразности, о повороте поверхности, о прогрессирующей составляющей погрешности шага резьбы и др.;
в) немонотонную (периодическую) составляющую погрешности; положение о немонотонной составляющей согласуется с представлениями о волнистости и шероховатости, о плавности и циклических погрешностях зубчатых колес, о периодических погрешностях шага резьбы;
г) случайную составляющую погрешности, как остаток аппроксимации функции погрешности.
В настоящее время модель параметра детали, как правило, определяется несколькими, практически не связанными между собой характеристиками: так, параметры поверхностей задают с помощью их предельных значений, допусков формы и предельных значений параметров шероховатости. Параметры связи поверхностей определяют предельными значениями размеров и допусками расположения поверхностей. Следует предположить, что вопросы обоснования выбора той или иной математической модели для описания параметров детали должны решаться на основе изучения процесса взаимодействий деталей в парах. Очевидно, что при дальнейшем изучении этих процессов, возможно, будет представлять более полные модели параметров с более совершенными способами задания немонотонных составляющих. |

