3.1. Параметры кода
Коды Рида-Маллера (РМ-коды) представляют собой двупараметрическое семейство блочных кодов с целыми неотрицательными параметрами m и r, для которых: 0 <= r < m. Характеристики РМ-кода: длина n = 2m; размерность k=Сn0+Сn1+….+Сnr, минимальное кодовое расстояние d = 2m-r, количество гарантированно исправляемых ошибок t = 2m-r-1-1.
При построении кодирующей матрицы будем использовать операцию побитового произведения векторов:  x x = (a1b1, … , anbn), где = (a1b1, … , anbn), где  = (a1, a2, ... an), = (a1, a2, ... an),  = (b1, b2, ... bn). Очевидно, что = (b1, b2, ... bn). Очевидно, что  x x = =  x x . .
Кодирующую матрицу G для параметров m и r определим как блочную матрицу вида: G = (G0| G1| …| Gr|)T, где Gi – специальная (Cmixn)-матрица. Именно, G0 = (1, 1, … , 1). В качестве столбцов матрицы G1 взяты все двоичные слова длины m, записанные в их естественном порядке. Матрица G1 имеет размерность Cm2 ? 2m.
Матрица G2 строится из строк матрицы G1 следующим образом: рассматриваются всевозможные побитовые произведения пар строк матрицы G1 и полученные результаты записываются как строки матрицы G2, причем порядок записи строк матрицы G2 несущественен, но обычно применяется лексикографическое упорядочение. Матрица G2 имеет размерность Cm2 ? 2m. Для любого l матрица Gl строится по аналогии с G2: рассматриваются всевозможные наборы по l строк матрицы G1 и для них вычисляются l-кратные побитовые произведения. Из полученных в результате новых строк формируется матрица Gl размерности Cml x 2m. Порядок записи строк матрицы Gl несущественен, но обычно применяется лексикографическое упорядочение. Отметим, что все строки матрицы G линейно независимы.
Пример 3. Рассмотрим m = 4, n = 24 = 16 и построим все блоки кодовой матрицы Рида-Маллера:
Для конкретного значения параметра r из этих блоков строится кодирующая матрица G = (G0| G1| …| Gr|)T.
3.2. Кодирование
Для кодов Рида-Маллера кодирование можно осуществлять простым умножением на кодирующую матрицу.
Пример 4. Рассмотрим случай m = 3, r = 1, n = 23-1 = 7, k=C30+C31 = 4. Тогда кодирующая матрица имеет вид:
Закодируем слово (1010): (1010)G =(11001100).
3.3. Мажоритарный декодер Рида
Отличительной особенностью декодера Рида является то, что по полученному из канала зашумленному кодовому слову  восстанавливается не истинное кодовое слово восстанавливается не истинное кодовое слово  , а непосредственно сообщение , а непосредственно сообщение  . Искомый информационный вектор . Искомый информационный вектор  =( =(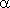 1,…, 1,…, 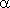 k) представляется в блочном виде ( k) представляется в блочном виде ( (0), (0),  (1), ... (1), ...  (r)), длина j-того блока равна Сmj. Декодирование производится по блокам справа налево, и при декодировании каждого следующего блока используются полученные ранее результаты. (r)), длина j-того блока равна Сmj. Декодирование производится по блокам справа налево, и при декодировании каждого следующего блока используются полученные ранее результаты.
Если r = 0, то РМ-код является кодом n-кратного повторения и декодирование производится обычным мажоритарным способом. Для остальных r построим последовательность алгоритмов, назовем их i-алгоритмами, которые позволяют декодировать i-тый блок сообщения и передавать управление на (i-1)-алгоритм.
i-Алгоритм.
1) Рассмотрим пришедшее по каналу слово   GFn(2) и представление ( GFn(2) и представление ( (0), (0),  (1), ... (1), ...  (r)) префикса информационного вектора (r)) префикса информационного вектора  . .
2) Анализ кодовой матрицы показывает, что биты кодового слова  представляют собой суммы некоторых битов информационного слова. Биты блока представляют собой суммы некоторых битов информационного слова. Биты блока  (i) будем восстанавливать справа налево. Для восстановления бита (i) будем восстанавливать справа налево. Для восстановления бита 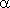 s блока построим контрольные суммы s блока построим контрольные суммы 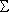 p, р = 1, 2, …, 2m-i, по 2i слагаемых, состоящих из битов кодового слова, таким образом, чтобы все информационные символы, отличные от p, р = 1, 2, …, 2m-i, по 2i слагаемых, состоящих из битов кодового слова, таким образом, чтобы все информационные символы, отличные от 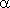 s, входили четное число раз в каждую контрольную сумму, а искомый информационный символ s, входили четное число раз в каждую контрольную сумму, а искомый информационный символ 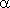 s входил в эту сумму нечетное число раз. Следовательно, при отсутствии ошибок все суммы s входил в эту сумму нечетное число раз. Следовательно, при отсутствии ошибок все суммы 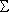 p должны совпадать между собой и совпадать с p должны совпадать между собой и совпадать с 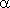 s. (Генерирование систем контрольных сумм в общем случае является трудной задачей, для конкретных значений параметров эти системы будут указаны в примерах. Вопросы программной реализации генерирования систем контрольных сумм рассмотрены А. Шамшиным [3] и В. Мкртичаном [4].) Вычислим по битам слова s. (Генерирование систем контрольных сумм в общем случае является трудной задачей, для конкретных значений параметров эти системы будут указаны в примерах. Вопросы программной реализации генерирования систем контрольных сумм рассмотрены А. Шамшиным [3] и В. Мкртичаном [4].) Вычислим по битам слова  значения значения 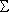 p, р = 1, 2, …, 2m-i. При условии, что ошибок на блок сделано не более чем 2m-r-1-1, простое голосование позволяет из набора p, р = 1, 2, …, 2m-i. При условии, что ошибок на блок сделано не более чем 2m-r-1-1, простое голосование позволяет из набора 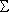 p выбрать правильное значение для p выбрать правильное значение для 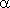 s. Проводя такие вычисления для каждого бита блока s. Проводя такие вычисления для каждого бита блока  (i), восстанавливаем весь блок. (i), восстанавливаем весь блок.
3) После восстановления блока  (i) проводим редукцию к (i-1)-алгоритму. А именно полагаем, что по каналу получено слово (i) проводим редукцию к (i-1)-алгоритму. А именно полагаем, что по каналу получено слово  ' = ' =  - -  (i)Gi и применим (i-1)-алгоритм для декодирования блока (i)Gi и применим (i-1)-алгоритм для декодирования блока  (i-1). (i-1).
3.4. Декодирование
Пусть m = 4, r = 2. Вычислим параметры кода: длина n = 16, размерность k = 11, минимальное кодовое расстояние d = 4, количество гарантированно исправляемых ошибок t = 1.
Пусть  = (01101011010) исходное информационное слово. Закодируем его = (01101011010) исходное информационное слово. Закодируем его  = =  G = (0101111111000110). Пусть на выходе канала получено слово G = (0101111111000110). Пусть на выходе канала получено слово  = (0111111111000110). Декодируем полученное слово = (0111111111000110). Декодируем полученное слово  . .
 = (a1, a2, ... a11); = (a1, a2, ... a11);  = =  G =(0101111111000110) G =(0101111111000110)
Символы a6,…..a11 декодируем с помощью 2-алгоритма..
Составим контрольные суммы
Проводим редукцию к 1-алгоритму:  ' = ' =  - (011010)G2 = (0111111111000110)- (0000010101100011) = (0111101010100101). К слову - (011010)G2 = (0111111111000110)- (0000010101100011) = (0111101010100101). К слову  ' применим декодер 1-го порядка. Результат: a5 = 1, a4 = 0, a3 = 1, a2 = 1. Осталось декодировать последний символ. Вычислим новое слово ' применим декодер 1-го порядка. Результат: a5 = 1, a4 = 0, a3 = 1, a2 = 1. Осталось декодировать последний символ. Вычислим новое слово  '' = '' =  ' - (a2, a3, a4, a5)G1 = (0111101010100101) – (1101)G1 = (0111101010100101) – (0101101010100101) = (0010000000000000). Следовательно, a1 = 0. ' - (a2, a3, a4, a5)G1 = (0111101010100101) – (1101)G1 = (0111101010100101) – (0101101010100101) = (0010000000000000). Следовательно, a1 = 0.
Информационное слово имеет вид (01101011010). 3.4. Упражнения
1. Составьте двоичное четырехбитное слово. Полученное слово закодируйте кодом Рида-Маллера с параметрами m = 3, r = 1.
2. Составьте двоичное слово из следующих значений: Ваше число (5 битов) и месяц (4 бита) рождения, Ваш возраст (5 бит), наличие у Вас младших сестры или брата (1-да, 0-нет), наличие у Вас старших сестры или брата (1-да, 0-нет). Полученное слово закодируйте кодом Рида-Маллера с параметрами m = 5, r = 2.
а) Внесите в кодовое слово одну ошибку и декодируйте рaезультат.
б) Внесите в кодовое слово число гарантированно исправляемых этим кодом ошибок и декодируйте результат. |