2.1. Параметры кода
Коды Хемминга представляют собой однопараметрическое семейство блочных бинарных кодов с параметром r = 2, 3, 4, … . Характеристики кода: длина n = 2r-1, размерность k = 2r-1-r, число проверочных символов r = n-k, минимальное кодовое расстояние d = 3, количество гарантированно исправляемых ошибок на блок t = 1. Проверочная матрица Нr,n кода Хемминга представляет собой (rxn)-матрицу, столбцами которой являются все ненулевые двоичные векторы длины n, записанные в естественном порядке. Коды Хемминга являются совершенными. 2.2. Кодирование
1) Выберем параметр r и вычислим значения n и k. Рассмотрим сообщение  = (a1, ... ak) = (a1, ... ak)  GFk (2). GFk (2).
2) Построим вспомогательную матрицу Мn,r = (Hn,r)T порядка (2r-1)xr .
3) Структура искомого кодового слова  = (b1, ... bn) = (b1, ... bn)  GFn (2) следующая: символы, индексы которых являются степенью двойки, т.е. GFn (2) следующая: символы, индексы которых являются степенью двойки, т.е. 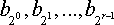 , – проверочные, а остальные символы вектора , – проверочные, а остальные символы вектора  совпадают с буквами сообщения совпадают с буквами сообщения  , записанными в естественном порядке. , записанными в естественном порядке.
4) Рассмотрим систему уравнений  Mn,r = Mn,r =  и, используя известные координаты вектора и, используя известные координаты вектора  , вычислим значения r=n-k проверочных символов. Отметим, что в каждое из уравнений входит только один проверочный символ. , вычислим значения r=n-k проверочных символов. Отметим, что в каждое из уравнений входит только один проверочный символ.
Пример 1. Рассмотрим случай r = 3, n = 7, k = 4. Закодируем слово  = 1010. Для этого построим вспомогательную матрицу М7,3, вычислим b3 = 1, b5 = 0, b6 = 1, b7 = 0, запишем и решим систему уравнений. = 1010. Для этого построим вспомогательную матрицу М7,3, вычислим b3 = 1, b5 = 0, b6 = 1, b7 = 0, запишем и решим систему уравнений.
Отсюда получаем, что  =1011010. =1011010. 2.3. Декодирование
1) Для полученного по каналу слова   GFn (2) вычислим GFn (2) вычислим  Мn,r = Мn,r =  (Hn,r)T. Если (Hn,r)T. Если  Мn,r = Мn,r =  , то делаем вывод, что , то делаем вывод, что  = =  – правильное кодовое слово и переходим на шаг 5. – правильное кодовое слово и переходим на шаг 5.
2) Если  Мn,r <> Мn,r <>  , то делаем вывод, что слово , то делаем вывод, что слово  содержит ошибку. Так как предполагается, что на блок попадает не более одной ошибки, то вектор ошибок имеет вид: содержит ошибку. Так как предполагается, что на блок попадает не более одной ошибки, то вектор ошибок имеет вид: 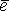 i = (0,0,...,1,...,0,0) (1 – на i-м месте). i = (0,0,...,1,...,0,0) (1 – на i-м месте).
3) В силу равенства  Мn,r = ( Мn,r = ( + + 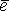 i)Mn,r = i)Mn,r = 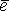 iMn,r, делаем вывод, что вектор iMn,r, делаем вывод, что вектор  Mn,r представляет собой двоичную запись номера i, указывающего на позицию ошибки. Вычисляем вектор ошибки Mn,r представляет собой двоичную запись номера i, указывающего на позицию ошибки. Вычисляем вектор ошибки 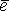 = = 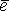 i. i.
4) Вычисляем правильное кодовое слово:  = =  + + 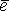 . .
5) По правильному кодовому слову  восстанавливаем сообщение восстанавливаем сообщение  , удаляя из , удаляя из  проверочные символы. проверочные символы.
Пример 2. Рассмотрим случай r = 3, n = 7, k = 4. Предположим на входе получено слово  = 1010010. Вычисляем синдром = 1010010. Вычисляем синдром  M7,3 = (1,0,0). Делаем вывод, что ошибка есть. По синдрому вычисляем (1,0,0)2 = 410 и делаем предположение, что неправильно принят четвертый символ. Следовательно M7,3 = (1,0,0). Делаем вывод, что ошибка есть. По синдрому вычисляем (1,0,0)2 = 410 и делаем предположение, что неправильно принят четвертый символ. Следовательно  = (1011010), = (1011010),  = (1010). = (1010).
2.4. Упражнения
1. Составьте двоичное слово из следующих значений: Ваш год (11 битов), число (5 битов) и месяц (4 бита) рождения, Ваш возраст (5 бит) и один произвольный бит. Полученное слово закодируйте методом Хемминга. Внесите в кодовое слово одну ошибку и декодируйте результат.
2. Методом Хемминга закодировать сообщение (11100101010), вычислив предварительно параметры кода. Построить для этих параметров кодирующую матрицу и с ее помощью проверить полученный результат |