Задача №3
ОПРЕДЕЛЕНИЕ ПЕРЕДАТОЧНОГО ОТНОШЕНИЯ ЗАМКНУТОГО
ДИФФЕРЕНЦИАЛЬНОГО МЕХАНИЗМА.
Краткие методические указания
Прежде
чем приступить к решению задачи №3, необходимо изучить раздел кинематического анализа зубчатых
механизмов по литературе [1]
с.145+146; [2] с.402+427; [3] с.52+57.
Замкнутые дифференциальные механизмы являются одним из типов эпициклических передач,
т.е. передач с подвижными осями. Получаются замкнутые дифференциальные механизмы из
обычных дифференциальных
механизмов, если два соосных вала соединяются (замыкаются) с ведущим или ведомым
валом через какую-либо передачу (простую зубчатую или планетарную). Замкнутые
дифференциальные механизмы имеют одну степень подвижности W=1, более высокий к.п.д., что объясняется возможностью
разделения передаваемой мощности на два параллельных потока и позволяет реализовывать
значительно большие крутящие моменты на выходе при малых габаритах привода. Такие передачи
используются, как правило, в силовых приводах.
Методика и пример решения задачи № 3
Для замкнутого
дифференциального зубчатого редуктора (рис.8) определить передаточное отношение от входного вала I к валу подвижного корпуса барабана и частоту вращения
барабана, если заданы числа зубьев колес Z1 = Z2 = Z5 = Z4 = 20, Z2 = Z4 = 38 и частота вращения вала n1 = 2000 мин-1.
Считать, что все колеса нулевые и имеют одинаковый
модуль.
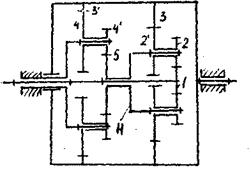
Рис.8. Замкнутый дифференциальный редуктор
1. Анализ
схемы механизма
В заданном механизме (см. рис.8) дифференциальная
часть образуется зубчатыми колесами
1,2,2,3 и водилом Н, жестко связанным
с колесом 5. Замыкающая часть - это
зубчатые колеса 5,4',4,3'. В замыкающей части блок колес 4 и 4 вращается относительно неподвижной оси.
2. Записываем основную формулу дифференциального механизма (формулу Виллиса)
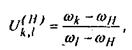 (11) (11)
где k, l-номера зубчатых колес; 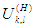 - передаточное отношение обращенного механизма, получающегося из дифференциального, при остановке водила Н; - передаточное отношение обращенного механизма, получающегося из дифференциального, при остановке водила Н;
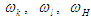 - угловые скорости колес с номерами К, l и водила Н. В механизме на рис.8 К=1, =3. В других механизмах задачи № 3 может быть К=1, =5. - угловые скорости колес с номерами К, l и водила Н. В механизме на рис.8 К=1, =3. В других механизмах задачи № 3 может быть К=1, =5.
Применительно к механизму на рис.8 формула (11) имеет вид
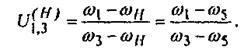 (12) (12)
3. Делим каждое слагаемое правой части на 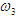 , являющуюся угловой скоростью барабана: , являющуюся угловой скоростью барабана:
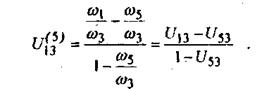 (13) (13)
4. Разрешаем уравнение (13) относительно искомого передаточного отношения U13
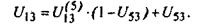 (14) (14)
5. Выражаем передаточные отношения 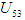 и
и 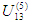 через числа зубьев колес: через числа зубьев колес:
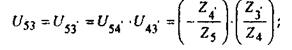 (15) (15)
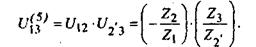 (16) (16)
После подстановки получим:
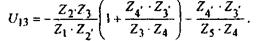 (17) (17)
6. Определяем неизвестные числа зубьев колес Z3 и Z3' из условий соосности:
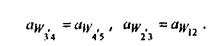
Выражаем межосевые расстояния через числа зубьев и модуль:
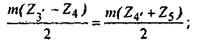
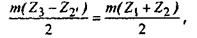
после преобразования получим:
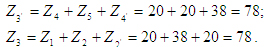
7. Подставляем численные значения в выражение (17):
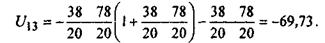
8.Определяем частоту вращения вала барабана
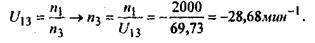
>>>Далее>>>
|

