Задача №4
ИССЛЕДОВАТЬ ДВИЖЕНИЕ МАШИННОГО АГРЕГАТА
ПОД ДЕЙСТВИЕМ ПРИЛОЖЕННЫХ СИЛ
Краткие методические указания
Перед решением задачи № 4 необходимо проработать раздел анализа движения механизма и машин по учебной
литературе: [1] с.304-349; [2] с.140-180;
[3] с.69-87.
Все
задачи данного типа решаются с помощью дифференциального уравнения движения агрегата, записанного в форме
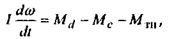
где l - приведенный к валу двигателя момент инерции агрегата; Md - приведенный к валу двигателя момент движущихся сил; Мс - приведенный к валу двигателя момент сил полезного сопротивления; MTn- приведенный к валу двигателя тормозной момент;
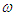 угловая скорость вала двигателя; t - время. угловая скорость вала двигателя; t - время.
Интегрируя уравнение (18), определяем зависимость 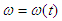 и остальные требуемые параметры. Скорость установившегося движения и остальные требуемые параметры. Скорость установившегося движения 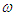 y получаем из соотношения предельным переходом. y получаем из соотношения предельным переходом.
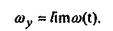
Методика и примеры решения задачи № 4
Пример № 1. Дано: I1 - момент инерции вала двигателя; I2 - момент инерции деталей, установленных на валу рабочей машины;
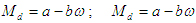
Приведя тормозной момент МТ и момент инерции I2 к валу двигателя, составить и решить дифференциальные уравнения движения вала двигателя в режимах разбега и выбега. Определить: зависимость угловой скорости 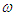 от времени t в режимах разбега и выбега; определить аналитически и графически угловую скорость установившегося движения; определить время выбега t. Построить графики: изменения угловой скоро¬сти от времени в режимах разбега и выбега; графики моментов движу¬щих сил и сил сопротивления в функции угловой скорости (графики по¬строить на общих осях координат, графически определить от времени t в режимах разбега и выбега; определить аналитически и графически угловую скорость установившегося движения; определить время выбега t. Построить графики: изменения угловой скоро¬сти от времени в режимах разбега и выбега; графики моментов движу¬щих сил и сил сопротивления в функции угловой скорости (графики по¬строить на общих осях координат, графически определить 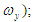
построить график мощности 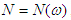 , развиваемой движущим моментом. , развиваемой движущим моментом.
1. Приводим к валу двигателя момент инерции деталей, установ¬ленных на валу рабочей машины. При проведении моментов инерции должно соблюдаться условие равенства кинетических энергий.
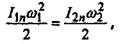
откуда
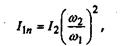 (19) (19)
где 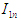 - приведенный к валу двигателя момент инерции деталей вала рабочей машины; - приведенный к валу двигателя момент инерции деталей вала рабочей машины;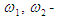
угловые скорости валов двигателя и рабочей машины; - передаточное отношение.
Окончательно имеем
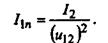 (20) (20)
Момент инерции агрегата приведенный к валу двигателя,
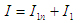 (21) (21)
2.Приводим к валу двигателя тормозной момент, приложенный к валу рабочей машины. При приведении моментов сил должно соблю¬даться условие равенства мгновенных мощностей.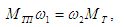
3.Рассмотрим 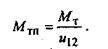 (22) движение агрегата в режиме разбега.
В этом режиме к валу двигателя приложены только момент дви¬жущих сил Мd и момент сил полезного сопротивления Мс. Уравнение (18) в этом случае имеет вид (22) движение агрегата в режиме разбега.
В этом режиме к валу двигателя приложены только момент дви¬жущих сил Мd и момент сил полезного сопротивления Мс. Уравнение (18) в этом случае имеет вид
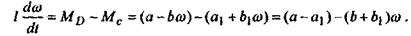
Обозначим 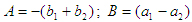 тогда тогда
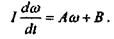
Разделим переменные:
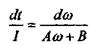
и интегрируем обе части уравнения
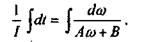
Справа – табличный интеграл вида
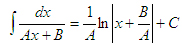
После интегрирования имеем
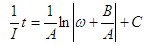
Для определения С используем начальное условие: при 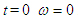
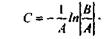
Окончательно, 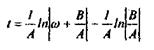 или или 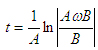 (24) (24)
Решив относительно 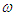 , получим , получим
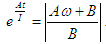
Обозначим 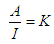 тогда тогда 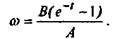 (25) (25)
Выражение (25) представляет собой зависимость угловой скорости от времени в режиме разбега.
4. Рассмотрим движение агрегата в режиме установившегося движения. Угловую скорость установившегося движения определим из выражения (25) предельным переходом
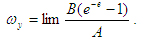 Поскольку
Поскольку 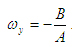 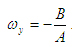 (26) (26)
Угловую скорость установившегося движения можно определить, зная, что в этом режиме МД=МС
Это условие используем для графического определения 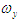 . .
5. Рассмотрим движение агрегата в режиме выбега.
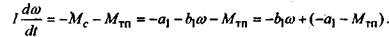
Обозначим 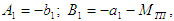 тогда тогда
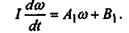
Выполнив действия, аналогичные предыдущим, получим:
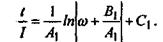
Для определения С1 используем начальные условия: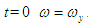 при при
Окончательно, 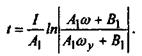 (27)
(27)
Обозначим 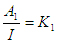 и, решив относительно и, решив относительно 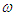 , имеем , имеем
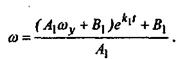 (28) (28)
Выражение (28) представляет собой зависимость угловой скорости от времени в режиме выбега.
Определим время выбега. Время выбега получаем из выражения (27), подставив
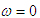
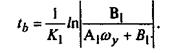 (29) (29)
7. Рекомендации для построения графиков
7.1. Графики 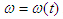 . Зададимся тремя-четырьмя промежуточными значениями . Зададимся тремя-четырьмя промежуточными значениями 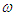 (между (между 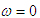 и и 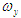 ), определим время из зависимостей (14) и (27). Полученные значения времени откладываем на оси абсцисс. Графики ), определим время из зависимостей (14) и (27). Полученные значения времени откладываем на оси абсцисс. Графики 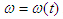 строим для режима разбега и отдельно для режима выбега. строим для режима разбега и отдельно для режима выбега.
7.2. Графики 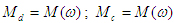 . Эти графики строим на общих осях координат для значений . Эти графики строим на общих осях координат для значений 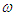 , выбранных выше. Здесь же определяется значение , выбранных выше. Здесь же определяется значение 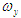 . .
7.3. График 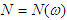 . График строится для тех же значений . График строится для тех же значений 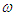 , определяем мощность по формуле , определяем мощность по формуле 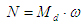
Виды графиков, построенных для конкретных значений Md и Мс, Мт, J, представлены на рис.9-12.
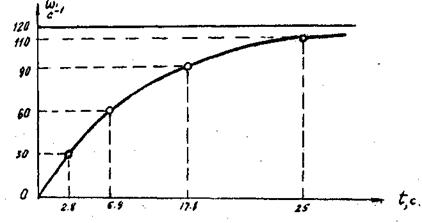
Рис.9. Зависимость 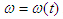 в режиме разбега в режиме разбега
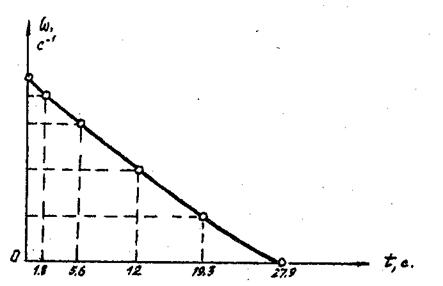
Рис.10. Зависимость  в режиме разбега в режиме разбега
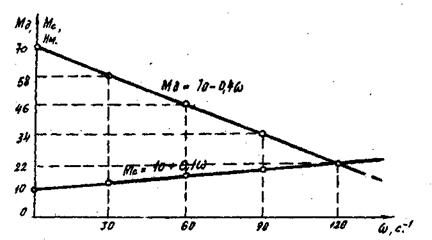
Рис.11. Зависимости 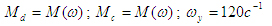
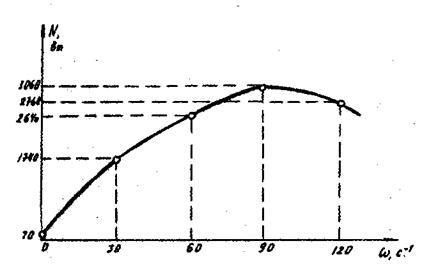
Рис.11. Зависимость 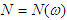
Пример № 2. Рассмотрим задачу, в которой 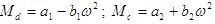 остальные параметры остались аналогичными предыдущему примеру. остальные параметры остались аналогичными предыдущему примеру.
1. Приводим к валу двигателя момент инерции деталей, уста¬новленных на валу рабочей машины (см. пример № 1)
2. Приводим к валу двигателя тормозной момент, приложенный к валу рабочей машины (см. пример № 1)
3. Рассмотрим движение агрегата в режиме разбега. Уравнение (18) имеет вид
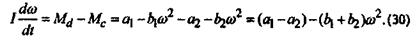
Обозначим 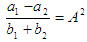 тогда уравнение (30) запишется как тогда уравнение (30) запишется как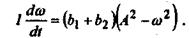 (31) (31)
Разделим переменные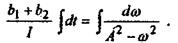
Справа записан табличный интеграл вида
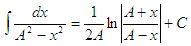
Интегрируя получаем
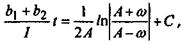 при
при 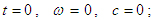
где 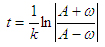 (32) (32)
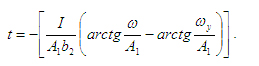
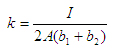
Из выражения (32)
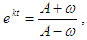 откуда откуда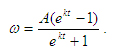 (33) (33)
Зависимость (33) представляет собой изменение угловой скорости от времени режима разбега.
4. Рассмотрим движение агрегата в режиме установившегося движения. Угловую скорость установившегося движения определим из выражения (33) предельным переходом
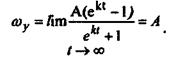 (34)
(34)
5.Рассмотрим движение агрегата в режиме выбега. Уравнение (18) имеет вид
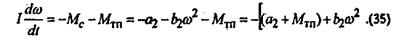
Обозначим 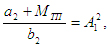 тогда уравнение (35) запишется как тогда уравнение (35) запишется как 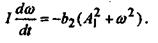 (36) (36)
Разделим переменные
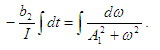
Справа имеем табличный интеграл вида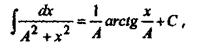 тогда тогда 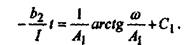
Произвольную постоянную определим из условия: при 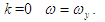
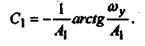
Окончательно
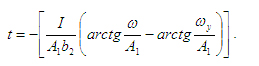
Обозначим 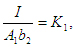 тогда, тогда,
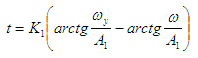 (37) (37)
Время выбега tв определим из условия
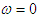
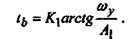 (38) (38)
Зависимость 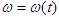 определим следующим образом: возьмем тангенс от левой и правой частей уравнения (37), используя тригонометрическую формулу тангенса равенства углов. определим следующим образом: возьмем тангенс от левой и правой частей уравнения (37), используя тригонометрическую формулу тангенса равенства углов.
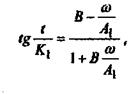 где где 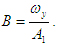
Решив относительно 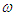 , имеем , имеем
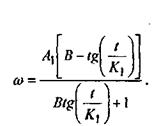 (39) (39)
Выражение (39) представляет собой зависимость угловой скорости от времени в режиме выбега.
>>>Далее>>>
|

