Задача №2
ВЫПОЛНИТЬ КИНЕМАТИЧЕСКИЙ АНАЛИЗ
ШАРНИРНО-РЫЧАЖНОГО МЕХАНИЗМА
Краткие методические
указания
К
кинематическому анализу шарнирно-рычажного механизма можно приступать только после решения задачи 1 и
изучения теоретического материала по учебникам: [1] с.73-96; с.550-568
[3] с.35-43; [2] с.70; 75-86; 308-321.
Исходными
для кинематического анализа механизма являются его кинематическая схема и закон движения входного звена.
Цель кинематического анализа:
изучение движения звеньев отдельных точек
без учета сил, вызывающих это движение.
Задачи кинематического
анализа механизмов сводятся к определению: 1) положений всех звеньев при любом
мгновенном положении входных звеньев; 2) траекторий и значений перемещений
точек механизма; 3) линейных скоростей и ускорений точек механизма; 4) углов скоростей и ускорений звеньев механизма.
Методы решения задач
кинематического анализа: графический, графоаналитический,
аналитический и экспериментальный.
При
решении задачи № 2 следует использовать графоаналитический метод.
Графоаналитический метод, основанный на составлении и графическом
решении векторных уравнений путем построения планов скоростей и ускорений, дает удовлетворительную для
инженерных расчетов точность, обладает простотой, наглядностью и достаточной
для практики информативностью.
Заметим,
что на плане скоростей (ускорений) механизма, векторы абсолютных скоростей (ускорений) выходят из
полюса Р плана скоростей (ускорений) механизма, а векторы
относительных скоростей (ускорений)
не проходят через полюс плана.
Методика
и пример решения задачи № 2
Выполнить кинематический анализ шарнирно-рычажного механизма (рис.7,а) при следующих исходных данных:
закон движения входного звена
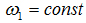 с частотой вращения n = 477,7 об/мин определяем по выражению с частотой вращения n = 477,7 об/мин определяем по выражению
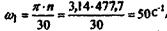 ход звена 3 равен Н3=170 мм; ход звена 3 равен Н3=170 мм;
линейные размеры:
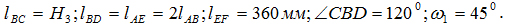
1 этап. Метрический синтез механизма. Звено АВ будет кривошипом, если
при вращении этого звена точка В пройдет последовательно положения BI и ВII.
Поэтому
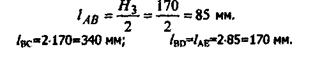
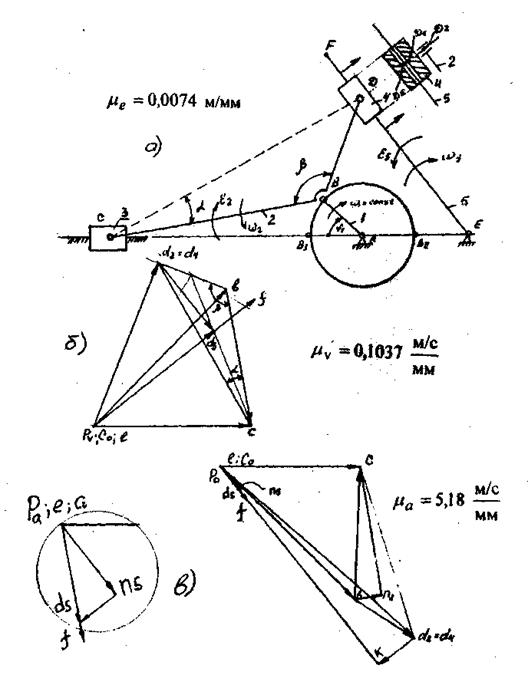
Рис.7. Схема шарнирно-рычажного механизма,
план скоростей и план ускорений
2 этап. Структурный анализ. Структурный анализ механизма проведен при решении задачи №
1. Было установлено:
1)
спроектирован механизм. Значит, с его кинематической схемой можно работать
дальше;
2) спроектированный
механизм второго класса. Следовательно, кинематический анализ можно проводить методами, предусмотренными рабочей
программой [5];
3) Формула
строения механизма имеет вид
.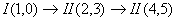
3 этап. План механизма. Изобразим на плане механизма звено 1 отрезком АВ=11,5
(рис.7а). Тогда масштаб плана
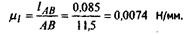 Длины остальных звеньев на плане будут равны
Длины остальных звеньев на плане будут равны
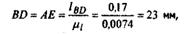 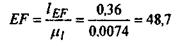 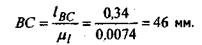
При построении плана элементы кинематических пар А и Е, а также ось направляющей в поступательной паре С1.
Выдержав угол 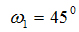 , вычерчиваем положение кривошипа. Методом засечек строим
остальные звенья механизма. , вычерчиваем положение кривошипа. Методом засечек строим
остальные звенья механизма.
4 этап.
Определение линейных скоростей точек и угловых скоростей звеньев механизма.
Определение скоростей начинаем с анализа механизма первого класса.
Механизм I класса (звенья I, О)
Модуль скорости точки B 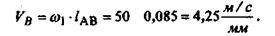
Изобразим скорость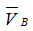 вектором вектором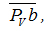 отложенным из некоторой точки Pv,
называемой полюсом плана скоростей (рис.7,б). Этот вектор направлен перпендикулярно АВ в сторону, соответствующую направлению угловой скорости отложенным из некоторой точки Pv,
называемой полюсом плана скоростей (рис.7,б). Этот вектор направлен перпендикулярно АВ в сторону, соответствующую направлению угловой скорости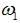 . .
Длина отрезка 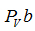 может быть выбрана произвольно.
В контрольной работе рекомендуется принимать может быть выбрана произвольно.
В контрольной работе рекомендуется принимать 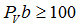 мм. Мы, исходя из
площади чертежа, примем мм. Мы, исходя из
площади чертежа, примем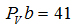 мм. Тогда
масштаб плана скоростей мм. Тогда
масштаб плана скоростей
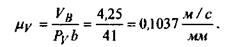
Переходим
к анализу первой структурной группы
Группа 2-го класса 2-го порядка 2-го вида (звенья 2-3)
Шаг 1 Определяем внутреннюю и крайние кинематические пары группы.
Внутренней будет вращательная кинематическая пара С . Крайними кинематическими парами
группы будут: вращательная пара В и поступательная пара C1. Парой В рассматриваемая
группа соединяется с предыдущей
кинематической цепью, а парой С1 - со стойкой.
Шаг 2 для точки С составляем два векторных уравнения
плоско-параллельного движения;
 (1) (1)
где - 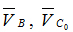 скорости точки С в переносном движении. Вектор скорости точки С в переносном движении. Вектор 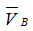 известен по величине и направлению из анализа
механизма первого класса. известен по величине и направлению из анализа
механизма первого класса.
Вектор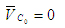 , так как точка С0 принадлежит стойке 0: , так как точка С0 принадлежит стойке 0: 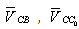 скорости точки С в относительном движении. Известно
только линии действия этих скоростей.
Так как точки С и В принадлежат одному звену 2, то вектор скорости точки С в относительном движении. Известно
только линии действия этих скоростей.
Так как точки С и В принадлежат одному звену 2, то вектор
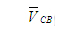 перпендикулярен прямой, соединяющей
эти точки, т.е. перпендикулярен прямой, соединяющей
эти точки, т.е.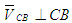
Так как точки С и С0 принадлежат разным звеньям 3 и 0, образующим
между собой поступательную пару, то вектор 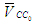 параллелен направляющей в поступательной паре С1, т.е. параллелен направляющей в поступательной паре С1, т.е.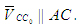
Шаг 3. Решаем систему уравнений (1).
Решаем первое уравнение системы (1). Для этого из полюса плана скоростей откладываем вектор 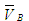 (он
был отложен на рис.7б). Вектор (он
был отложен на рис.7б). Вектор 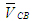 записан
после вектора записан
после вектора 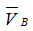 Следовательно, вектор Следовательно, вектор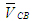 начинается
в конце вектора начинается
в конце вектора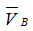 . .
Отсюда построение: через точку б плана скоростей проводим прямую, перпендикулярную звену СВ, представляющую собой линию
действия вектора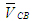
Решая второе уравнение системы (1), из полюса Pv плана скоростей откладываем вектор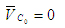 (нуль-вектор). Получаем, что точка С0 будет в полюсе плана.
Вектор (нуль-вектор). Получаем, что точка С0 будет в полюсе плана.
Вектор 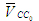 записан
в уравнении после вектора записан
в уравнении после вектора 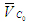 .Отсюда построение: через точку С0 плана скоростей проводим прямую, параллельную направляющей СА. Это - пиния действия вектора .Отсюда построение: через точку С0 плана скоростей проводим прямую, параллельную направляющей СА. Это - пиния действия вектора 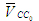 . Точка пересечения построенных линий действия векторов . Точка пересечения построенных линий действия векторов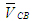 и и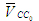 (точка С на
рис.7б) определяет решение системы (1). (точка С на
рис.7б) определяет решение системы (1).
Шаг 4. Рассматриваемой
группе принадлежит точка Д2,
обозначенная на схеме механизма
(см.рис.7а). Положение её на плане скоростей найдем, используя свойство подобия плана скоростей. Для этого на плане скоростей строим ?cbd2, ?ACBD и сходственно с ним расположенный. Соединив точку d2 с полюсом Pv плана, получим вектор абсолютной
скорости точки D2,
принадлежащей звену 2. Полученная фигура Pvсbd2 называется планом
скоростей звена 2, вектор Рvc - план скоростей звена 3. Планом
скоростей группы звеньев 2-3 является фигура Pvсbd2
Шаг 5.Используя план
скоростей группы, находим:
абсолютные скорости точек:

относительные сорости точек:
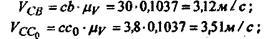
угловые скорости звеньев:
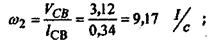
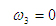 , так как звено 3 не вращается. , так как звено 3 не вращается.
Здесь
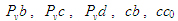 – отрезки на плане скоростей, мм; – отрезки на плане скоростей, мм; 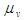 - масштаб плана - масштаб плана
скоростей,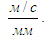
Для определения направления
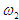 необходимо с
плана скоростей перенести вектор необходимо с
плана скоростей перенести вектор 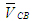 в точку С на схему механизма и посмотреть, куда этот вектор будет вращать точку С вокруг
точки В, Видим, что в точку С на схему механизма и посмотреть, куда этот вектор будет вращать точку С вокруг
точки В, Видим, что 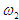 направлено против хода часовой стрелки. Теперь переходим к анализу второй структурной группы. направлено против хода часовой стрелки. Теперь переходим к анализу второй структурной группы.
Группа 2-го класса 2-го порядка 3-го вида (звенья 4-5)
Шаг 1. Внутренняя пара - поступательная пара D1 крайние кинематические
пары -это вращательные пары D и Е.
Шаг 2. Векторные уравнения плоскопараллельного
движения. Во внутренней кинематической
паре группы Ассура 3 вида (и у группы 5 вида) есть две точки: D4 принадлежит
звену 4 (см. рис.7а) и Ds принадлежит звену 5. Так как
линейные размеры звена 4 не заданы, то звено 4 можно рассматривать как материальную точку, совпадающую с точкой D2.
Поэтому 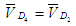 Неизвестна
скорость точки D5. Для неё
и надо писать векторные уравнения. Они имеют вид: Неизвестна
скорость точки D5. Для неё
и надо писать векторные уравнения. Они имеют вид:
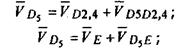 (2) (2)
где, 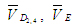 известные скорости точки Ds в переносном движении. Причем известные скорости точки Ds в переносном движении. Причем 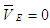 так как точка Е принадлежит одновременно звену 5 и стойке 0. Скорость так как точка Е принадлежит одновременно звену 5 и стойке 0. Скорость 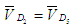 найдена при
анализе группы 2-3; скорости точки D5 в относительном движении. Известны
только линии действия этих скоростей. Так как точки D4 и D5 принадлежат разным звеньям
4 и 5, образующим между собой
поступательную пару, то вектор найдена при
анализе группы 2-3; скорости точки D5 в относительном движении. Известны
только линии действия этих скоростей. Так как точки D4 и D5 принадлежат разным звеньям
4 и 5, образующим между собой
поступательную пару, то вектор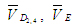 параллелен направляющей
в поступательной паре, т.е. параллелен направляющей
в поступательной паре, т.е.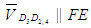
Так как точки D5 и Е принадлежат одному звену 5, то вектор
 перпендикулярен прямой, соединяющей точки D5 и Е, т.е.
перпендикулярен прямой, соединяющей точки D5 и Е, т.е.
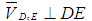
Шаг 3. Решение системы (2) осуществляем построением из
полюса Pv плана скоростей правой части каждого из уравнений
системы. Так, решая первое уравнение
системы (2), из полюса откладываем в масштабе 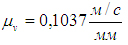 вектор вектор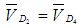 (он уже отложен на рис.76).
Через точку d4 плана
скоростей проводим прямую, параллельную звену 5, которая представляет собой линию
действия вектора Решая второе уравнение системы (2), из полюса Pv плана скоростей откладываем вектор (он уже отложен на рис.76).
Через точку d4 плана
скоростей проводим прямую, параллельную звену 5, которая представляет собой линию
действия вектора Решая второе уравнение системы (2), из полюса Pv плана скоростей откладываем вектор 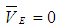 (нуль-вектор). Получаем, что точка е будет в полюсе плана. Через точку е проводим прямую, перпендикулярную звену 5, представляющую собой линию действия вектора (нуль-вектор). Получаем, что точка е будет в полюсе плана. Через точку е проводим прямую, перпендикулярную звену 5, представляющую собой линию действия вектора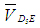 .Точка пересечения
построенных линий действия .Точка пересечения
построенных линий действия 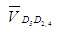 точка d5 на рис.76) определяет решение системы (2). точка d5 на рис.76) определяет решение системы (2).
Шаг 4.
Рассматриваемой группе принадлежит точка Е.
Положение её на плане скоростей найдем,
используя свойство подобия плана скоростей. Для этого составим пропорцию
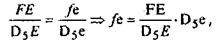
где FE, D5E - отрезки схемы механизма (рис.7а), мм; fе, d5e- отрезки на плане скоростей,
мм. Полученные
векторы 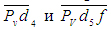 есть планы
скоростей соответственно звеньев 4 и
5, а фигура есть планы
скоростей соответственно звеньев 4 и
5, а фигура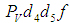 план скоростей группы звеньев 4-5. план скоростей группы звеньев 4-5.
Шаг
5. По плану скоростей находим
абсолютные скорости точек:
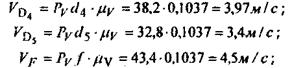
Относительные скорости точек:
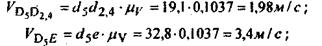
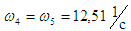 так как звенья 4 и 5 образуют поступательную пару. Здесь так как звенья 4 и 5 образуют поступательную пару. Здесь 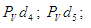 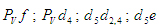 - отрезки на плане скоростей в мм. - отрезки на плане скоростей в мм.
Для определения направления 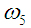 необходимо с плана скоростей перенести вектор необходимо с плана скоростей перенести вектор 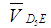 в точку D5 на схему механизма и посмотреть, куда этот вектор будет вращать точку D5 вокруг точки Е. Видим, что в точку D5 на схему механизма и посмотреть, куда этот вектор будет вращать точку D5 вокруг точки Е. Видим, что 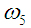 направлено по ходу часовой стрелки. направлено по ходу часовой стрелки.
5 этап. Определение линейных ускорений точек и угловых ускорений звеньев механизма. Определение ускорений начина¬ем с анализа механизма первого класса.
Механизм 1 класса (звенья 1,0)
Так как 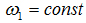 то для точки В кривошипа 1 то для точки В кривошипа 1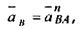
где 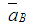 - вектор абсолютного ускорения точки В; - вектор абсолютного ускорения точки В; 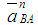 - вектор нормального ускорения точки В при вращении её относительно точки А. - вектор нормального ускорения точки В при вращении её относительно точки А.
Вектор 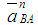 направлен по радиусу к центру вращения (от точки В к точке А). направлен по радиусу к центру вращения (от точки В к точке А).
Модуль его равен
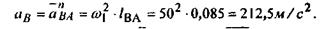
Изобразим 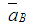 ускорение вектором ускорение вектором 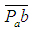 отложенным из не которой точки Ра, называемой полюсом плана ускорений (рис.7в). Длина отрезка отложенным из не которой точки Ра, называемой полюсом плана ускорений (рис.7в). Длина отрезка 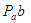 может быть выбрана произвольно. В контрольной работе рекомендуется принимать может быть выбрана произвольно. В контрольной работе рекомендуется принимать 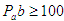 мм. мм.
Примем 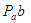 =41мм. Тогда масштаб плана ускорений. =41мм. Тогда масштаб плана ускорений.
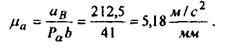
Структурная группа Ассура. (звенья 2,3)
Переходим к построению плана ускорений группы Ассура 2-го класса 2-го порядка 2-го вида, образованной звеньями 2-3.
Для точки С внутренней кинематической пары группы Асура напишем два векторных уравнения плоско-параллельного движения
 (3)
где
(3)
где 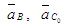 - ускорения точки С в переносном движении. Вектор - ускорения точки С в переносном движении. Вектор 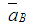 известен по величине и направлению из анализа механизма первого класса. Вектор известен по величине и направлению из анализа механизма первого класса. Вектор 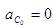 , так как точка С0 принадлежит стойке 0; ; , так как точка С0 принадлежит стойке 0; ; 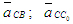 - ускорения точки С в относительном движении. - ускорения точки С в относительном движении.
Так как точки С и В принадлежат одному звену, то вектор 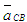 надо раскладывать на нормальную и тангенциальную составляющие, т.е. надо раскладывать на нормальную и тангенциальную составляющие, т.е.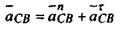 (4) где
(4) где 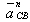 - нормальная составляющая ускорения вращения точки С шатуна 2 относительно точки В. - нормальная составляющая ускорения вращения точки С шатуна 2 относительно точки В.
Модуль этого ускорения
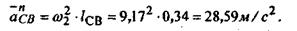
Вектор 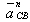 параллелен звену СВ и направлен к центру вращения этого звена, т.е. от точки С к точке В. параллелен звену СВ и направлен к центру вращения этого звена, т.е. от точки С к точке В.
На плане ускорений 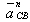 отложим вектором отложим вектором
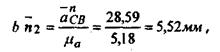
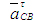 - тангенциальная составляющая ускорения вращения точки С ша¬туна 2 относительно точки В. Известна только линия действия этого вектора - прямая, перпендикулярная звену СВ - мгновенному радиусу вращения точки С относительно точки В. - тангенциальная составляющая ускорения вращения точки С ша¬туна 2 относительно точки В. Известна только линия действия этого вектора - прямая, перпендикулярная звену СВ - мгновенному радиусу вращения точки С относительно точки В.
Так как точки С и Со принадлежат разным звеньям, образующим поступательную пару, то
, 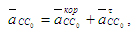 где где 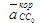 - вектор ускорения Кориолиса, определяемый по величине как - вектор ускорения Кориолиса, определяемый по величине как 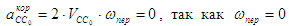 ,(5) так как - угловая скорость вращения переносной среды (т.е. направляющей в поступательной паре); ,(5) так как - угловая скорость вращения переносной среды (т.е. направляющей в поступательной паре);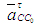 - ускорение поступательного движения ползуна 3 по стойке. Известна лишь линия действия этого ускорения - прямая, параллельная направляющей в поступательной паре. - ускорение поступательного движения ползуна 3 по стойке. Известна лишь линия действия этого ускорения - прямая, параллельная направляющей в поступательной паре.
Подставим уравнения (4) и (5) в систему (3), получим:
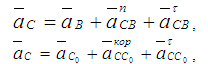 (6) (6)
Решаем систему (6) построением слагаемых правой части.
Из полюса Pa плана ускорений откладываем в масштабе 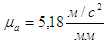 . Он был уже отложен на рис.7в. Получим точку b. Далее согласно первому уравнению системы (6) из точки b пла¬на ускорений откладываем вектор . Он был уже отложен на рис.7в. Получим точку b. Далее согласно первому уравнению системы (6) из точки b пла¬на ускорений откладываем вектор 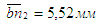 и через полученную точку n2 проводим прямую, перпендикулярную звену СВ. Это линия действия вектора и через полученную точку n2 проводим прямую, перпендикулярную звену СВ. Это линия действия вектора 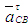 . Решаем второе уравнение системы . Из полюса Ра плана ускорений откладываем вектор . Решаем второе уравнение системы . Из полюса Ра плана ускорений откладываем вектор 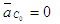 . К нему прибавляем вектор . К нему прибавляем вектор 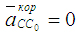 . Заметим, что отложив два вектора (), мы продолжаем находиться в полюсе Pa плана. Через конец вектора . Заметим, что отложив два вектора (), мы продолжаем находиться в полюсе Pa плана. Через конец вектора 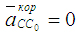 (т.е. через полюс плана) проводим горизонталь. Это - линия действия вектора .
Пересечение двух построенных на плане ускорений линий действия ускорений и даст точку с, определяющую решение системы векторных уравнений.
Положение точки D2 на плане ускорений найдем, используя свойство подобия плана ускорений. (т.е. через полюс плана) проводим горизонталь. Это - линия действия вектора .
Пересечение двух построенных на плане ускорений линий действия ускорений и даст точку с, определяющую решение системы векторных уравнений.
Положение точки D2 на плане ускорений найдем, используя свойство подобия плана ускорений.
Для этого на плане ускорений строим
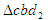 ?СВD и сходственно с ним
расположенный. Соединив точку d2 с полюсом Ра плана, получим вектор абсолютного ускорения точки D2 ?СВD и сходственно с ним
расположенный. Соединив точку d2 с полюсом Ра плана, получим вектор абсолютного ускорения точки D2
Полученный вектор - есть план ускорений звена 3, а фигура 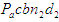 - план ускорений звена 2 и всей группы, образованной звеньями 2 и 3. - план ускорений звена 2 и всей группы, образованной звеньями 2 и 3.
Используя план ускорений группы, находим: абсолютные ускорения точек:
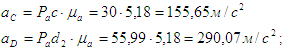
относительные ускорения точек:
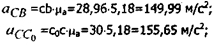
тангенциальное ускорение точки С
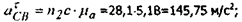
угловые ускорения звеньев
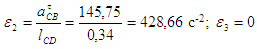 так как звено 3 не вращается. так как звено 3 не вращается.
Здесь 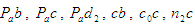 - отрезки на плане ускорений, мм. - отрезки на плане ускорений, мм.
Для определения направления 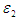 необходимо с плана скоростей перенести вектор необходимо с плана скоростей перенести вектор 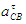 в точку С на схему механизма и посмотреть, куда этот вектор будет вращать точку С вокруг точки В. Видим, что в точку С на схему механизма и посмотреть, куда этот вектор будет вращать точку С вокруг точки В. Видим, что 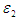 направлено против хода часовой стрелки. направлено против хода часовой стрелки.
Переходим к анализу второй структурной группы, образованной звеньями 4 и 5.
Выше было показано, что векторные уравнения надо писать для точки D 5 . Они имеют вид:
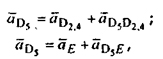 (7) (7)
где
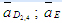 - известные ускорения точки D5 в переносном движении.
- известные ускорения точки D5 в переносном движении.
Причем 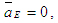 так как точка Е принадлежит одновременно звену 5 и стойке 0. так как точка Е принадлежит одновременно звену 5 и стойке 0.
Ускорение
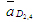 найдено при анализе группы 2-3; найдено при анализе группы 2-3;
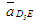 ускорения точки D5 в относительном движении. ускорения точки D5 в относительном движении.
Так как точки D5 и D4 принадлежат разным звеньям 4 и 5, а эти звенья образуют между собой поступательную пару, то
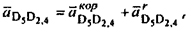 (8) (8)
Где
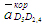 - вектор ускорения Кориолиса, определяемый по величине так: - вектор ускорения Кориолиса, определяемый по величине так:
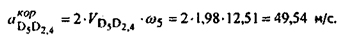
Для определения направления вектора 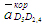 необходимо повернуть вектор скорости необходимо повернуть вектор скорости 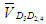 вокруг основания этого вектора на 90° в сторону вокруг основания этого вектора на 90° в сторону 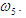 . .
На плане ускорений вектор 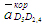 изобразится отрезком изобразится отрезком
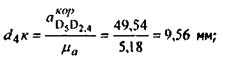
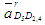 - ускорение поступательного движения кулисы (точки D5) относительно камня (точки D4). Известна лишь линия действия этого вектора - прямая, параллельная FЕ - линии хода кулисы относительно камня. Так как точки D5 и Е принадлежат одному звену 5, то - ускорение поступательного движения кулисы (точки D5) относительно камня (точки D4). Известна лишь линия действия этого вектора - прямая, параллельная FЕ - линии хода кулисы относительно камня. Так как точки D5 и Е принадлежат одному звену 5, то
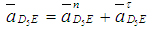 (9) (9)
где 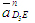 - нормальная составляющая ускорения вращения точки D5 кулисы 5 относительно точки Е. - нормальная составляющая ускорения вращения точки D5 кулисы 5 относительно точки Е.
Модуль этого ускорения
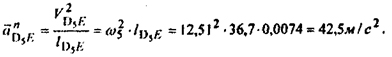
Вектор 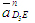 параллелен звену DE и направлен к центру вращения этого звена, т.е. от точки D5 к точке Е. На плане ускорений параллелен звену DE и направлен к центру вращения этого звена, т.е. от точки D5 к точке Е. На плане ускорений 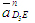 отложим вектором отложим вектором
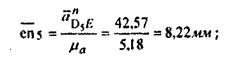
где 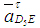 - тангенциальная составляющая ускорения вращения точки D5 кулисы относительно точки Е.
Известна только линия действия этого вектора – перпендикулярно звену FE. Подставим уравнения (8) и (9) в систему (7). Получим: - тангенциальная составляющая ускорения вращения точки D5 кулисы относительно точки Е.
Известна только линия действия этого вектора – перпендикулярно звену FE. Подставим уравнения (8) и (9) в систему (7). Получим:
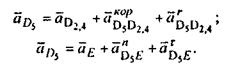 (10) (10)
Решаем систему построением слагаемых правой части. Из полюса Paплана ускорений откладываем в масштабе
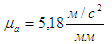 вектор вектор 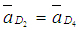 (см. рис.7в). Из точки d4 плана ускорений откладываем вектор (см. рис.7в). Из точки d4 плана ускорений откладываем вектор 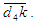 . Через точку к проводим прямую, параллельную FE. Это - линия действия вектора . Через точку к проводим прямую, параллельную FE. Это - линия действия вектора 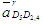 .
Решая второе уравнение системы из полюса Pa плана ускорений откладываем вектор .
Решая второе уравнение системы из полюса Pa плана ускорений откладываем вектор 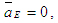 (нуль-вектор). Получаем, что точка е будет в полюсе плана. Из точки е откладываем вектор (нуль-вектор). Получаем, что точка е будет в полюсе плана. Из точки е откладываем вектор 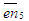 через конец которого (точку n5) проводим прямую, перпендикулярную звену FE. Это - линия действия тангенциального ускорения через конец которого (точку n5) проводим прямую, перпендикулярную звену FE. Это - линия действия тангенциального ускорения 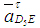 . .
Точка пересечения построенных линий действия векторов 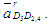 и и 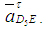 - (точка ds) определяет решение системы .
Положение на плане ускорении точки F найдем, используя свойство подобия плана ускорений. Для этого составим пропорцию: - (точка ds) определяет решение системы .
Положение на плане ускорении точки F найдем, используя свойство подобия плана ускорений. Для этого составим пропорцию:
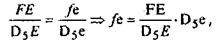
где 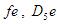 отрезки на плане ускорений, мм. отрезки на плане ускорений, мм.
Полученныйвектор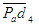 есть план ускорений звена 4, а фигура есть план ускорений звена 4, а фигура 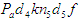 - план ускорений группы и звена 5 . - план ускорений группы и звена 5 .
По плану ускорений находим:
абсолютные ускорения точек:
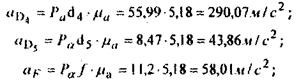
относительные ускорения точек:
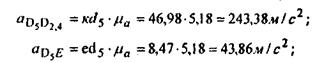
тангенциальное ускорение:
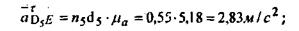
угловые ускорения звеньев:
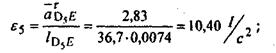
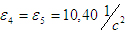 так как звенья 4 и 5 образуют между собой поступательную пару. так как звенья 4 и 5 образуют между собой поступательную пару.
Здесь 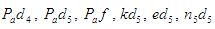 - отрезки на плане ускорений, мм. - отрезки на плане ускорений, мм.
Для определения направления 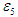 необходимо с плана ускорений перенести вектор необходимо с плана ускорений перенести вектор 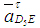 (вектор (вектор 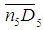 ) точку Ds на схему механизма и посмотреть, куда этот вектор будет вращать точку D5 вокруг точки Е. Видим, что ) точку Ds на схему механизма и посмотреть, куда этот вектор будет вращать точку D5 вокруг точки Е. Видим, что 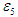 направлено против хода часовой стрелки. направлено против хода часовой стрелки.
В заключение решения задачи 2 определим характер движения звеньев механизма. Звено АВ вращается с постоянной угловой скоростью (по условию задачи). Звено ВС вращается замедленно, т.к. 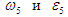 направлены в противоположные стороны. Звено С движется поступательно и ускоренно, так как векторы направлены в противоположные стороны. Звено С движется поступательно и ускоренно, так как векторы 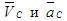 сонаправлены. Звенья 4 и 5 вращаются замедленно, так как сонаправлены. Звенья 4 и 5 вращаются замедленно, так как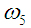 и и 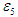 направлены в противоположные стороны. Звено 4 (камень) движется поступательно по звену 5 (кулисе) замедленно, так как векторы направлены в противоположные стороны. Звено 4 (камень) движется поступательно по звену 5 (кулисе) замедленно, так как векторы 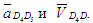 и ( и ( 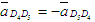 ) направлены в противоположные стороны. ) направлены в противоположные стороны.
>>>Далее>>>
|
|

