Задача №1
ОПРЕДЕЛИТЬ СТЕПЕНЬ ПОДВИЖНОСТИ МАШИННОГО АГРЕГАТА И ВЫПОЛНИТЬ СТРУКТУРНЫЙ АНАЛИЗ СХЕМЫ МЕХАНИЗМА РАБОЧЕЙ МАШИНЫ.
Приступая к решению задачи №1, необходимо изучить теорети¬ческий материал по учебникам и учебным пособиям: [1] стр. 19-63; [2] стр. 18-59; [3] стр. 3-51.
Цель структурного анализа механизмов - изучение строения механизмов.
Задачи структурного анализа:
1. Установить, является ли данная кинематическая цепь механизмом.
2. Определить класс механизма, чтобы правильно выбрать метод кинематического и силового расчета данного механизма.
3. Написать формулу строения механизма и тем самым указать последовательность кинематического и силового расчетов исследуемого механизма.
Исходным для структурного анализа механизма является его ки¬нематическая схема.
Условимся на кинематических схемах стойку механизма обозна¬чить нулем, подвижные звенья - арабскими цифрами, а кинематические пары - латинскими буквами.
Методика и пример решения задачи № 1
Для данного машинного агрегата (рис.1), состоящего из двигате¬ля, передаточного механизма (рис.2) и рабочей машины (рис.3), опре¬делить степень подвижности. Для схемы механизма рабочей машины провести полный структурный анализ.
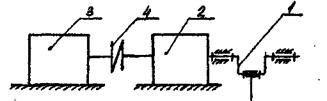
Рис 1. Машинный агрегат: 1— кривошип рабочей машины (см. рис.3)
2 - передаточный зубчатый механизм (см. рис.2), 3 - двигатель,
4 - соединительная муфта
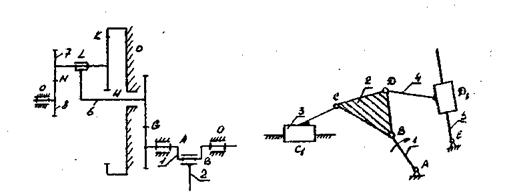
Рис.2 Схема придаточного механизма Рис.3. Схема механизма рабочей машины
1. Определение степени подвижности машинного агрегата
1.1. Нумеруем звенья и обозначаем кинематические пары.
При этом учитываем, что на заданной схеме передаточного ме¬ханизма кривошип, а следовательно, и жестко связанное с ним зубчатое колесо имеют номер 1, а образуемая этим звеном кинематическая пара со стойкой обозначена буквой А.
Последовательность нумерации звеньев может быть произвольной. Получили число подвижных звеньев n = 8.
1.2. Выделяем кинематические пары, определяя их наименова¬ние и класс по И.И. Артоболевскому (табл.1).
Таблица 1
Обозначение кинематической пары
|
А
|
В
|
С
|
С1
|
D
|
D1
|
Е
|
G
|
Н
|
L
|
К
|
М
|
N
|
Звенья, образующие кинематическую пару
|
1,0
|
1,2
|
2,3
|
3,0
|
2,4
|
4,5
|
5,0
|
6,1
|
6,0
|
7,6
|
7,0
|
7,8
|
8,0
|
Наименование
пары
|
Вращ.
|
Вращ.
|
Вращ.
|
Пост.
|
Вращ.
|
Пост.
|
Вращ.
|
Зубчат.
|
Вращ.
|
Вращ.
|
Зубчат.
|
Зубчат.
|
Вращ.
|
Класс пары
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
4
|
5
|
5
|
4
|
4
|
5
|
1.3. Определяем степень подвижности по формуле П.Л. Чебышева
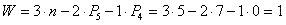
где n = 8 - число подвижных звеньев; Р5 = 10 - число кинематических пар 5-го класса; Р4 = 3 - число кинематических пар 4-го класса..
2. Полный структурный анализ схемы механизма рабочей машины
2.1. Наименование звеньев по характеру движения: 0 - стойка; 1 кривошип; 2 - шатун; 3 - ползун; 4 - шатун, кулисный камень; 5 - коро¬мысло, кулиса.
2.2. Кинематические пары (табл.2).
Таблица 2
Обозначение кинематической пары
|
А
|
В
|
С
|
C1
|
D
|
D1
|
Е
|
Звенья,
образующие кинематическую пару
|
1,0
|
1,2
|
2,3
|
3,0
|
2,4
|
4,5
|
5,0
|
Наименование пары
|
Вращ. низшая
|
Вращ. низшая
|
Вращ. низшая
|
Пост. низшая
|
Вращ. низшая
|
Пост. низшая
|
Вращ. низшая
|
Класс пары
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
2.3. Степень подвижности механизма
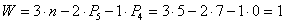
где n = 5 - число подвижных звеньев; Р5 = 7 - число кинематических пар 5-го класса; Р4 = 0 - число кинематических пар 4-го класса.
2.4.Структурная схема (рис.4)
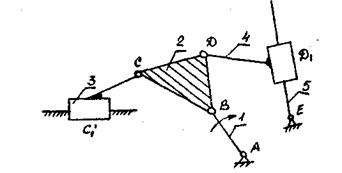
Рис.4 Структурная схема механизма
Заметим, что на структурных схемах имеет смысл звено, входящее в три и более кинематические пары, вычерчивать соответствующим жестким многоугольником, а ползуны и кулисные камни заменять соответствующим контуром.
2.5 Механизм первого класса (Рис.5)
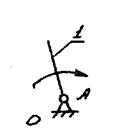
Рис.5 Механизм первого класса
2.6.Структурные группы Л.В.Ассура
2.6.1.Находим звено, наиболее удаленное от входного. Это звено 5.
2.6.2.Выделяем группу второго класса. Предполагаемую группу Асура образуют звенья 5 и 4.
2.6.3.Проверяем, будет ли эта цепь в данном механизме группой Асура. Отсоединяем мысленно звенья
5 и 4 вместе с кинематическими парами E, D1, D. Оставшаяся кинематическая цепь (рис.6) будет замкнута и степень W её свободы будет равна единице. Значит, выделили группу Л.В.Ассура.
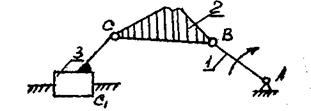 Рис.6. Кинематическая цепь
Рис.6. Кинематическая цепь
Для оставшейся кинематической цели (см. рис.6) повторяем шаги 2.6.1 - 2.6.3
и убеждаемся, что звенья 2 и 3 вместе с кинематическими парами В, С и С1
являются группой Л.В.Ассура. Таким образом, для рас¬сматриваемого примера имеем:
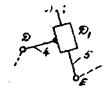 группа Л.В. Ассура 2-го класса 2-го порядка 3-го вида
группа Л.В. Ассура 2-го класса 2-го порядка 3-го вида
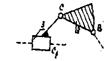 группа Л.В. Ассура 2-го класса 2-го порядка 2-го вида группа Л.В. Ассура 2-го класса 2-го порядка 2-го вида
2.7. Класс всего механизма – второй
2.8. Формула строения механизма:
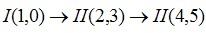
>>>Далее>>>
|

