Глава 17. ПРИМЕРЫ РАСЧЁТА НЕКОТОРЫХ ЭЛЕМЕНТОВ И ПАРАМЕТРОВ СИСТЕМ АВТОМАТИКИ

17.1. Датчики

Потенциометрический датчик

Рассчитать потенциометрический датчик с реостатной схемой включения для измерения механического усилия F=25 H с погрешностью не более d =0,1 Н. Коэффициент чувствительности пружины, используе- мой в качестве воспринимающего элемента, равен к=2 мм/Н, напряжение питания U=12 В с частотой f=400 Гц . Построить статическую характери- стику рассчитанного датчика.

1. Составим схему потенциометрического датчика (рис.17.1).

2. В качестве вторичного прибора выбираем вольтметр магнито-электрической системы со шкалой U max =15 В и сопротивлением R п =10 4 Ом .

3. Примем, что при силе в 25 Н показание вольтметра U п =12 В , следовательно, статический коэффициент преобразования – чувствитель- ность датчика (цена деления вольтметра) составляет

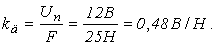
4. Рассчитаем длину рабочей части потенциометра

x max = к ? F = 2 мм/Н ? 25 Н = 50 мм .

5. Найдем длину всей намотки потенциометра

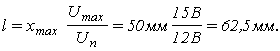
6. Исходя из величины погрешности измерения d , найдем шаг намотки D l

D l= d ? к=0,1Н ? 2 мм/Н=0,2 мм.

7. Выбор провода проведем по величине его диаметра d и удельного сопротивления r . Возьмем нихромовый провод d=0,15 мм , .

S=0,0176 мм 2 (площадь поперечного сечения), r =1,1 Ом мм 2 /м . При этом необходимо выполнение условия d< D l , оно у нас выполняется.

8. Величину сопротивления потенциометра R находим, исходя из условия

R=(0,1...0,125)R п , т.е. R=0,125 ? 10 4 Ом=1250 Ом .

9. Рассчитаем величину сопротивления рабочей части потенцио- метра R x ,

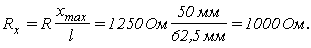
10. Определим теперь конструктивные параметры потенциометра: длину обмоточного провода L обм . , общее число витков потенциометра W , длину одного витка L ср , диаметр каркаса D .

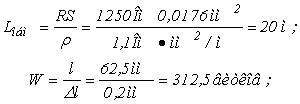
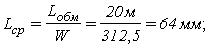
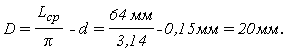
11. Рассчитаем плотность тока j и мощность, рассеиваемую на потенциометре Р,

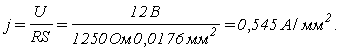
Допустимая плотность тока лежит в пределах от 2 до 3 А/мм 2 .

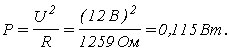
12. Проведем проверку теплового режима работы потенциометра, для чего находим площадь боковой поверхности S об и удельную боковую поверхность охлаждения s о

S об = p ? D ? l= p ? 2 см ? 6,25 см=39 см 2 ;

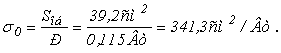
Для нормального теплового режима работы значение s о должно быть более 5...7 см 2 /Вт . Это условие выполняется.

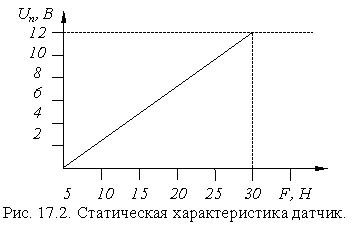
13.Построим статическую характеристику данного датчика (рис.17.2).

Фотоэлектрический датчик

Рассчитать реостатную схему включения фотоэлектрического датчика ФС - К1 (фоторезистор). Определить и построить зависимость изменения напряжения на резисторе R от освещенности Е.

Паспортные данные ФС - К1:

к о =6 мА/лм ? В - чувствительность;

S=28,8 мм 2 - площадь чувствительного элемента;

a =0,81 - коэффициент;

Р max =0,2 Вт.

Освещенность Е изменяется в пределах 0...3000 лк., напряжение питания 12 В .

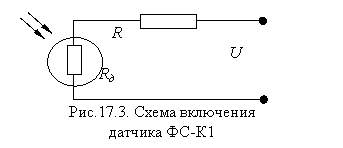
1. Построим схему включения датчика ФС - К1(рис.17.3).

2. Определим мощность, выделяемую на фоторезисторе ФС - К1

Р д =U д ? I д,

где I д =к 0 ? U д ? S ? E a .

Тогда Р д =к о ? U д 2 ? S ? Е a ? P max , а величина максимального падения напряжения U дmax на сопротивлении фоторезистора R д при максимальной освещенности Е=3000 лк может быть вычислена так:

U дmax =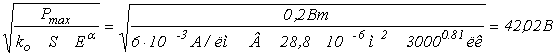

Примем U д =10 В , тогда величина фототока в фоторезисторе

I д =6мА/лм ? В ? 10В ? 28,8мм 2 ? 3000 0.81 лк=1,14мА ,

а величина мощности, выделяемой при этом фототоке имеет, такую величину

Р д =1,14 ? 10 -3 А ? 10В=0,0114 Вт.

3. Зная эти величины, нетрудно вычислить величину резистора R из соотношения

U= U R +U д ,

U=I д ? R+U д ,

откуда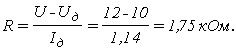

4. Теперь нетрудно рассчитать зависимость U R =f(E) и по ней построить график.

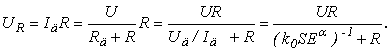
5.Данные расчета сведены в таблицу (табл.17.1)

Таблица 17.1

Примечание. Вывод размерности в формуле для расчета U д (п.2)

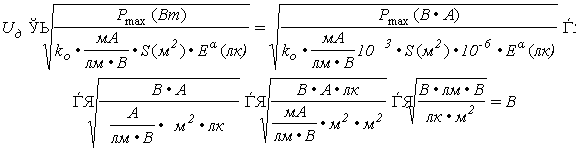
так как лм/м 2 = лк.

Емкостный датчик

Рассчитать и построить статическую характеристику емкостного датчика для измерения перемещения d = 1...5 мм, имеющего площадь пластины S=20 см 2 и напряжение питания U=48 В с частотой f=1000 Гц . Построить зависимость изменения коэффициента чувствительности ёмко- сетного датчика k в от величины перемещения его пластины d .

• 

1. Построим схему включения емкостного датчика (рис.17.4).

2. Определим величину тока, текущего через датчик д .

,

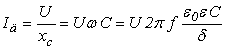где e о =8,85 ? 10 -12 Ф/м , e = 1.

3. Для расчета чувствительности датчика используем формулу

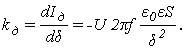
4. Расчетные данные сведем в таблицу (табл.17.2)

Таблица 17.2

Термометр сопротивления

Рассчитать термометр сопротивления с мостовой схемой включи- гния для измерения температуры t =20...200 ° С. Сопротивление датчика при t о =20 ° С R(t o )=10 Ом , а температурный коэффициент a =4 ? 10 -3 1/ ° С .

Напряжение питания U=24 В, f=50 Гц.

1. Построим схему включения датчика (рис.17.5)

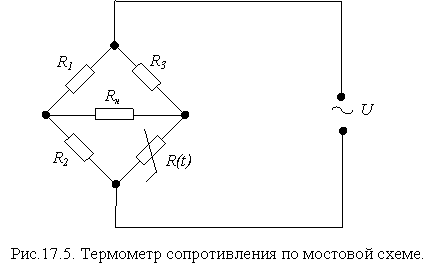
2.Зависимость сопротивления датчика от температуры выражается следующей формулой:

R(t)=R(t o )[1+ a ? (t-t o )]

3. Наибольшую мощность на выходе датчика (резистор R н ) получаем при условии R н =R 1 =R 2 =R 3 =R( t 0 )=10 Ом .

4. Найдем зависимость тока в нагрузке датчика (резистор R н ) I н =f(t ° ) на основании схем замещения холостого хода (хх) и короткого замыкания (кз), рис.17.6.

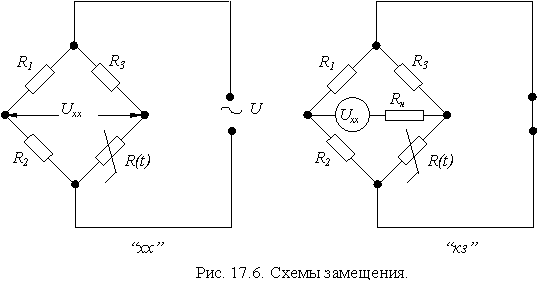
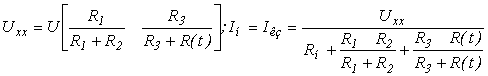
5. В выражении для R(t) п.2 подставим исходные данные и получим

R(t)=10 ? [1+4 ? 10 -3 ? 1/ ° C ? (t-t o )] Ом .

После преобразований получим выражения для напряжения холостого хода U хх и тока в нагрузке I н :

;

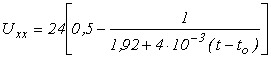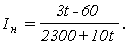
Результаты расчета сведём в таблицу (табл.17.3).

6. Находим теперь коэффициент чувствительности мостовой схемы датчика

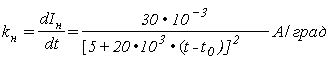
7. Результаты расчета приведены в табл.17.3.

Таблица 17.3.

Зависимость I н , U xx и k от t ( 0 C )

Датчики температуры на термисторе

Термистор включён в реостатную схему для измерения темпера- туры в пределах от 20 до 100 ° С. Паспортные данные термистора таковы: .

R н =5.1 ? 10 3 Ом - величина сопротивления при t н =20 ° С ;

Р max =5 мВт - максимальная рассеиваемая мощность;

В=2000 ° К - коэффициент.

Зависимость сопротивления термистора от температуры выражается следующей формулой:

R(t)=R ? e B./ t , (*)

причем В и t должны быть выражены в К.

t=t н =273 ° +20 ° =293К,

имеем е В./t ? R=R(t)=R н =5,1 ? 10 3 Ом .

В общем случае

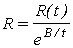
и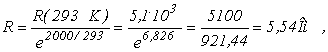

тогда исходное выражение (*) примет вид

R(t)=5,54 ? е В /t .

1. Построим cхему включения термистора (рис.17.7, где U =48 B , f =1000Гц

2. Определим величину падения напряжения U T на термисторе R(t) при t=100 ° С или t=373 К при условии, что Р Т ? Р max , где Р Т - мощность, выделяемая на термисторе.

откуда

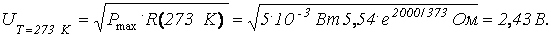
Расчет сделан для t=100 ° C , т.к. при этой температуре будем иметь максимальную мощность по сравнению с меньшими значениями температуры.

3. Рассчитаем теперь величину сопротивления резистора R ? ,

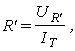
где U R ? - падение напряжения на резисторе R ? , I Т - ток цепи термистора.

U R ? =U-U Т , ,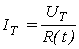

откуда R ? =(U/U Т -1)R(t) .

При t=100 ° С=373К, R(373К)=5,54 ? е 2000/373 =1180,77Ом . Тогда получим R ? =(48/2,43 -1) ? 1180,77=22143 Ом .

Примем R ? =22 кОм .

4. Далее находим зависимость U R ? (t),

U R ? (t)= R ? ? I Т (t);

; .

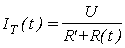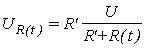5. Найдем теперь зависимость коэффициента чувствительности термистора от температуры k д (t)

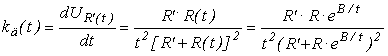
6. Расчетные данные представлены в таблице (табл.17.4)

Таблица17.4

Индуктивный датчик

Рассчитать и построить статическую характеристику индуктивного датчика с мостовой схемой включения для измерения перемещений d =1...5мм .

Параметры датчика:

S=30 см 2 - сечение магнитопровода;

W=3000 - число витков;

R=3000 Ом - активное сопротивление обмотки.

Датчик питается переменным напряжением U=48В с частотой f=100Гц .

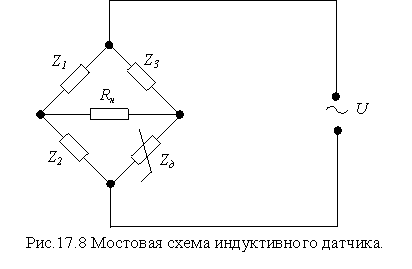1. Построим схему датчика (рис.17.8).

•  Рассчитаем индуктивность датчика по формуле

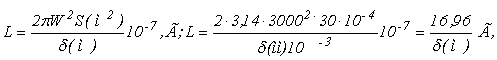
где Г –генри, размерность индуктивности L .

•  Находим величину индуктивного сопротивления обмотки датчика

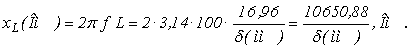
•  Параметры мостовой схемы определяют из условия

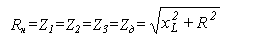
При минимальном зазоре d =1 мм и максимальной мощности на выходе сбалансированного моста( U н =0 ) имеем:

L=16,96/1,0=16,96Г;
x L =10650,88/1,0=10,651 кОм.

5. На основании схем для режимов “ хх ” и “ кз ” (см. стр. 177) имеем

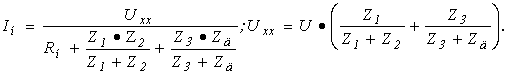
6. При определении коэффициента чувствительности датчика k д полагаем его активное сопротивление равным нулю

R д =0

Численные значения к д возможно найти аналитически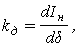 либо, построив кривую, графически .

7. Результаты расчета сведены в таблицу

Таблица 17.5

Зависимость I н от d

17.2 Дифференциальные уравнения и передаточные функции звеньев

Передаточная функция гидравлического демпфера

Возьмем для иллюстрации в качестве звена системы автоматического регулирования гидравлический демпфер (рис.17.9).

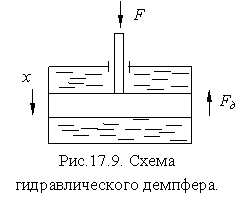
В качестве входной величины примем силу F , а выходной величины – перемещение поршня х . Влиянием массы подвижных частей поршня пренебрегаем. Найдем передаточную функцию этого звена.

Очевидно, что силе F , действующей на демпфер, будет противостоять 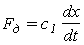сила демпфирования , где с 1 – коэффициент демпфирования. Он пропорциоален площади пропускного отверстия.

Имеем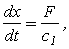

откуда на основе перехода к изображениям имеем

рх=кF,

где к=с -1 , и далее, так как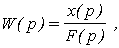

получаем: х=кF/p и

Теперь несколько усложним задачу и к поршню демпфера подсоединим возвратную пружину, также пренебрегая влиянием массы подвижных частей и принимая за входную величину силу воздействия F , а за выходную величину - перемещение точки М (рис.17.10).

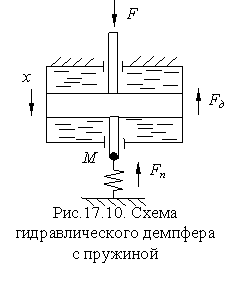
Прежде всего составим уравнения равновесия сил, действующих в системе

F = F д + F п ,

где 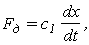а F п =с 2 х,

тогда

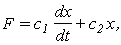
где с 1 - коэффициент демпфирования, с 2 - коэффициент упругости пружины.

Разделим уравнение на с 2 :

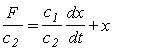
и произведем переход к изображению

к ? F=T 1 p x+x ,

где к=с 2 -1 ; Т 1 =с 1 /с 2 , или к ? F=(T 1 p+1)x .

Теперь нетрудно записать выражение для передаточной функции:

Дифференциальное уравнение движения поршня гидравлического демпфера с пружиной

Взяв за основу условие предыдущей задачи ,составим уравнение движения поршня. Построим схему поршня с цилиндром и пружиной (рис.17.11).

Так же как и ранее составим уравнение равновесия сил

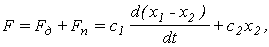
где х 1 -х 2 - перемещение поршня относительно цилиндра;

х 2 - перемещение точки М .

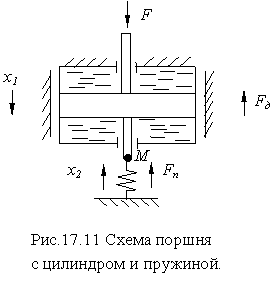
Запишем теперь это уравнение так

разделим на с 1 и получим

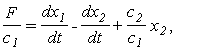
или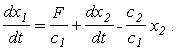

Перейдем от оригиналов к изображения

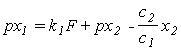
или рх 1 =к 1 F+к 2 ( t р - 1)х 2 , (*)

где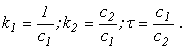

17.3. Синтез и анализ динамики систем автоматического регулирования 

В практике эксплуатации сельскохозяйственных машин очень часто помимо создания новых систем автоматического регулирования необходимо совершенствовать и уже работающие. Потому студенты должны иметь некоторые практические навыки по синтезу и анализу динамики САР. Для этого необходимо решить следующие задачи:

•  выбрать критерий оптимальности динамики САР;

•  определить динамические параметры объекта регулирования;

•  рассчитать оптимальные динамические характеристики регулятора;

•  составить структурную схему и найти уравнение динамики САР;

•  произвести оценку устойчивости работы САР;

•  проверить качество регулирования.

Чтобы решить поставленную задачу, необходимо знать:

• переходную характеристику объекта регулирования (она снимается экспериментально или имеется её аналитическое выражение);

•  характер возмущающего воздействия со стороны регулирующе- го органа (приведенного к входу объекта регулирования) и его величину;

•  требования к качеству регулирования.

Рассмотрим поэтапно решение этой задачи.

Выбор критерия динамики САР

Критерии оптимальности динамики любой САР представляют собой наиболее важные требования, предъявляемые к качеству регули- рования. В качестве критериев чаще всего используют следующие:

•  отсутствие регулирования ;

•  20% - ное перерегулирование;

•  минимум интегральной квадратичной оценки регулирования;

•  минимум времени регулирования.

Перечисленные критерии позволяют получить САР с соответствующими переходными процессами по возмущающему воздействию или по задающему воздействию.

На рис.17.12 показаны переходные процессы соответственно каждому из критериев, где а -без перерегулирования; б - с 20%-ным перерегулированием; в- с минимальной интегральной квадратичной ошибкой; г - с минимальным временем регалирования; 1-по возмуще- нию; 2-по задающему воздействию.

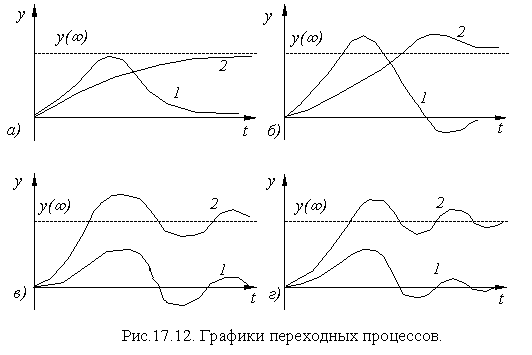
Применяя в качестве критериев оптимальности динамики САР критерий отсутствия перерегулирования или минимума времени регулирования, мы добиваемся наибольшей устойчивости, но здесь возникают большие динамические ошибки.

Для критерия минимальной интегральной квадратичной ошибки регулирования мы получаем минимальные потери, возникающие в процессе регулирования, но необходимо в этом случае сметь точную и надежную информацию о свойствах объекта регулирования и регуляторе. Следует быть очень осторожным, т.к. в САР, рассчитанной с использованием этого критерия переходной процесс затухает слабо и возможен переход системы под воздействием из устойчивого состояния в неустойчивое.

Определение динамических параметров объекта регулирования

К динамическим характеристикам объекта регулирования относятся: к - коэффициент передачи; Т - постоянная времени объекта;

t - постоянная запаздывания .

Постоянная времени объекта Т может быть охарактеризована как временная характеристика, показывающая как, за какое время выходной сигнал достигнет определенного значения, а постоянная запаздывания t показывает с какой временной задержкой от момента приложения входного сигнала начинает интенсивно изменятся выходная ве- личина.

Существует много методов определения динамических характеристик объекта регулирования : по его теоретическим выражениям, по экспериментальным переходным, импульсным, частотным или спектральным характеристикам, но наиболее часто применяемым на практике является метод определения динамических характеристик объекта регулирования по его экспериментальной переходной характеристике. Это наиболее простой метод с точки зрения экспериментального снятия переходной характеристики и расчета динамических характеристик объекта. Однако при существенных преимуществах снятая экспериментально переходная характеристика недостаточно точна на начальном участке в силу следующих причин: не всегда высокая чувствительность измери- тельной аппаратуры, сильное влияние шумов при малых значениях входного и выходного сигналов, значительные отклонения регулируемой величины в ходе эксперимента.

При использовании данного метода для определения динамических характеристик объекта следует руководствоваться табл. 17.7.

Таблица 17.7

Примечание: М - точка перегиба; U - регулирующее воздействие; 1( t - t ) – единичная функция с запаздыванием; Т 0 – постоянная времени; t 0 – время запаздывания; e 0 – скорость разгона; k 0 - коэффициент передачи.

Расчет оптимальных динамических характеристик регулятора

Расчет оптимальных динамических характеристик регулятора может быть произведен по отношению времени запаздывания к постоянной времени объекта, по амплитудно-фазовым или логарифмическим частотным характеристикам объекта, а также путем моделирования на ЭВМ и другими методами.

Наиболее употребляемым методом является первый метод – расчет оптимальных динамических характеристик регулятора по отношению времени запаздывания к постоянной времени объекта. Этот метод дает возможность определить основные динамические характеристики: тип регулятора и закон регулирования, передаточную функцию и динамические параметры настройки регулятора (табл. 17.8).

Порядок расчета следующий. По динамическим параметрам объекта регулирования (у нас это объект первого порядка с запаздыванием) находим отношение 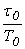для объекта с самовыравниванием или 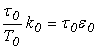для объекта без самовыравнивания. Далее рассчитываем отношение t p / t o , где t p - требуемое время регулирования.

Затем по таблице 17.9 для выбранного типа критерия оптимально- стидинамики САР выбираем типы регулятора с подходящим быстродействием.

При выборе типа регулятора нужно учитывать следующие рекомендации.

Наибольшим быстродействием обладает П - регулятор. Пример- но такое же (несколько меньше) быстродействие имеет ПИД регулятор. Примерно в два раза меньше, чем у первых двух, имеет ПИ - регулятор, а быстродействие И и РПС - регуляторов (РПС - релейный постоянной скорости) соответственно еще меньше. После этого из отобранных регуляторов выбирают такой, который соответствует требуемой точности регулирования, характеру возмущения и наиболее прост.

Таблица 17.8

Примечание :П - пропорциональный; И – интегральный регулятор;ПИ – пропор-ционально-интегральный; ПИД - пропорционально-интегрально-дифференциальный; РД - релейный двухпозиционный; РПС - релейный постоянной скорости; U - регулирующее воздействие; х - отклонение регулируемой величины от заданного значения (рассогласование); k р - коэффициент передачи регулятора; Т И - время изодрома; Т д - время предварения; U m - полный ход регулирующего органа в %; D - полузона возврата; d - полузона нечувствительности; U m /T им - скорость перемещения регулирующего органа; Т им - время полного хода регулирующего органа.

Таблица 17.9

При этом учитываются следующие особенности:

- П - регулятор не может устранить статическую ошибку регулирования (имеется в виду статическая ошибка регулирования, превы- шающая полузону нечувствительности регулятора). Ее величина пропоциональна возмущению, воздействующему на объект. Поэтому П – регулятор рекомендуется использовать при малых возмущениях.

- РД - (релейный двухпозиционный) регулятор следует применять при малых возмущениях, допуская наличие незатухающих колеба- ний регулируемой величины. Этот регулятор также является достаточно простым.

- И, ПИ, РПС - регуляторы следует применять для случаев плавного изменения прикладываемого к объекту возмущения. Причем И и РПС - регуляторы применяют только для объектов с самовыравниванием. Эти регуляторы сложнее, чем П и РД - регуляторы.

- ПИД - регулятор имеет смысл применять при резких и частых возмущениях, но это наиболее сложный регулятор.

Теперь для выбранного типа регулятора записываем реализуемый им закон регулирования (см. табл. 17.8), его передаточную функцию и подлежащие определению динамические параметры настройки регуля- тора. Такая методика и приведенные формулы позволяют рассчитать динамические параметры настройки регулятора при воздействии возмущения со стороны регулирующего органа, т.е. когда возмущение заменено на эквивалентное ему перемещение регулирующего органа. Следует отметить, что если динамические характеристики объекта по каналам воздействия возмущения и регулирования будут сильно отличаться друг от друга, то мы получим значения динамических параметров настройки регулятора с большими погрешностями.

Далее по приведенным в таблице 17.9 формулам для выбранного типа регулятора и критерия оптимальности САР (табл. 17.10) рассчиты- ваем динамические параметры настройки регулятора.

Таблица 17.10

Окончание табл.17.10.

Примечания:

В случае, когда динамические характеристики объекта по каналам воздействия возмущения и регулирования будут сильно различаться между собой, это приведет к существенным погрешностям в определении динамических параметров настройки регулятора.

Для РД - регулятора следует задаться возможными значением регулирующего воздействия U м , которое больше величины возмущения z , потом из приведенного неравенства (примеч. 1), устанавливающего точность регулирования, определить максимальную величину полузоны возврата D В , при которой это неравенство выполняется. Далее, подставив полученную величину D В в уравнение для расчета периода автоколеба- ний Т а (примеч.2), вычислить его значение. Если найденное значение периода автоколебаний не удовлетворяет предъявляемым к нему требованиям, то нужно уменьшить U м таким образом, чтобы оно оставалось больше величины z , и повторить проведенные вычисления. При уменьшении величины U м происходит увеличение периода автоколебаний Т а , при уменьшении D В-снижение амплитуды и периода автоколебаний.

В случае РПС - регулятора сначала вычисляют величину полузоны нечувствительности D н , имея в виду, что с ее уменьшением точность и время регулирования возрастают. Потом согласно выбранному критерию оптимальности настройки САР находят скорость перемещения регулирующего органа U m /Т им , а по ней вычисляют величину времени полного хода регулирующего органа Т им . При этом, если окажется, что технически обеспечить такую величину Т им невозможно, то следует выбрать другое значение D н и провести расчет еще раз.

Если не удастся технически реализовать рассчитанные динамические параметры настройки регуляторов вследствие их малых значений, то в контур регулирования перед исполнительным механизмом включа- ется ступенчатый импульсный прерыватель. В этом случае следует до-полнительно рассчитать такие динамические параметры настройки: период подачи импульсов Т и , и длительность одного импульса t и , которые связаны таким соотношением

, (*)

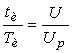где 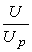- отношение оптимального регулирующего воздействия к р еа- лизуемому.

Для П, И, ПИ и ПИД регуляторов

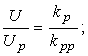
для РД - регулятора

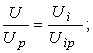
для РДС - регулятора

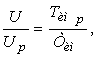
где к рр , U мр и Т имр реализуемые значения величин к р , U м и Т им соответственно.

При расчете Т ц и t n для РПС регулятора нужно учитывать, что перемещение регулирующего органа за время Т ц не должно вызывать изменение регулируемой величины, превышающее величину зоны нечувствительности 2 D н . Поэтому в этом случае сначала рассчитывают величину Т и

где U м - полный ход регулирующего органа, а потом еже из формулы (*) находят значение t n .

Следует особо обратить внимание, что значения Т и и t и нельзя выбирать произвольно. Их следует выбирать из ряда реализуемых значений. Например, для ступенчатого импульсного прерывателя СИП-01:

Т и (с)=15; 30; 60; 120

t и (с)=1; 2; 3;...; 7 или 8 ;9;...; 14; 23; 24;...; 29;...; 53; 54;...; 59

и 113; 114;...; 119.

При этом различие между рассчитанными и реализуемыми зна- чениями Т и и t и не должны превышать точность расчета основных дина-мических параметров настройки регуляторов, которая лежит в пределах до 15%.

И в заключении расчета следует уточнить значения основных динамических параметров настройки регулятора согласно выражению(*).

Наиболее распространенными методами представления динами- ческих свойств САР являются графический и аналитический.

Первый метод - составление структурной схемы САР, второй - составление уравнений динамики.

Как известно структурная схема САР - то условное графиче- ское изображение ее в виде цепи, определенным образом соединенных звеньев и их передаточных функций. На рис.17.13 показана структурная схема САР с ПИ-регулятором в объекте первого порядка с запаздыванием и самовыравниванием, где е - t р - запаздывающее звено; к р / Т и р – интегрирующее звено; к о /Т о р+1 - апериодическое звено первого порядка.

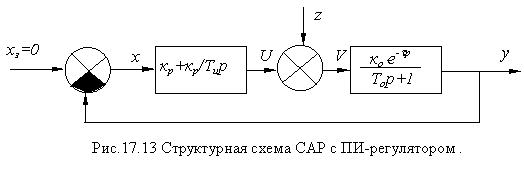
Эта схема составлена на основании принципа регулирования по отклонению. По этому принципу были разработаны вышерассмотренные методы расчета динамических характеристик регулятора. Возможно построение и по другим принципам регулирования.

Уравнение динамики САР можно записывать в виде дифференциального уравнения в классической или операторной форме. Вторая форма считается наиболее предпочтительной из-за ее компактности и уравнение легко получить из структурной схемы.

Вот это уравнение:

[Т и Т о р 2 +Т и р+(Т и р+1)к р к о е - t р ]y=к о е - t р Т и р ? z;

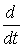заменить оператор р на , а y и z -на временные переменные y(t) и z(t).

Под устойчивостью САР понимается ее способность возвращаться установившееся положение после устранения внешних воздействий, нарушивших это состояние. Данное условие является необходимым, но не достаточным.

Для оценки устойчивости линейных САР используют корневые, частотные и некоторые другие методы. Эти методы позволяют разделить показатели устойчивости САР (например, степень устойчивости, показатель колебательности, запасы устойчивости по модулю и фазе). Здесь следует провести процедуру, описанную в п.7.2.

Для оценки устойчивости нелинейных САР следует применять иные методы, например, предложенные в работе [13].