Развёртку конуса вращения можно построить по его параметрам. Она представляет собой сектор круга, радиус которого равен длине образующей - R; длина ограничивающей сектор дуги равна длине окружности основания конуса, а центральный угол сектора равен

a = (r / R) 360°, где r - радиус основания.

Поскольку при развёртывании конической поверхности её аппроксимируют пирамидальной, то мы рассмотрим развёртку поверхности конуса общего вида с круговым основанием (рис. 318).

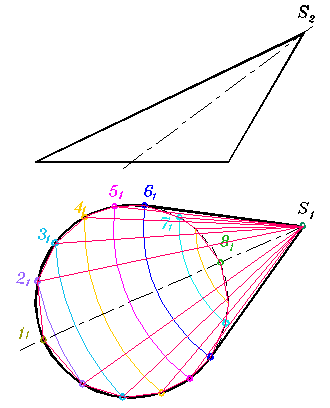
Рис. 318

Для закрепления изучаемого материала решите задачи: №59 и №61

Заменим коническую поверхность пирамидальной с возможно большим количеством граней (не менее 8-ми). На направляющей конуса выбирают ряд точек. Их удобно выбирать проведением дуги из горизонтальной проекции вершины, чтобы получить симметричную развёртку. Если красным цветом соединить точки деления направляющей между собой, то получится вписанный многоугольник. Если вершины полученного многоугольника соединить с вершиной конуса, получится вписанная пирамида (рис. 318 а), рёбра которой являются образующими. При построении вписанной гранной поверхности считаем грани вписанной пирамиды треугольниками, боковые стороны которых составляют образующие, а основанием является хорда окружности основания. Обычно не строят проекции вписанной пирамиды, просто имеют её в виду.

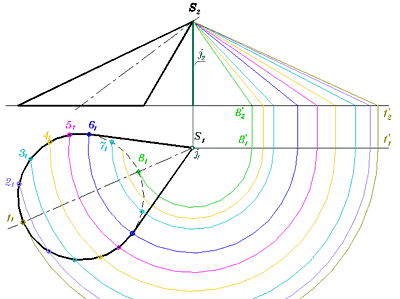
Рис. 318-а

Длину каждой образующей рекомендуется определять вращением вокруг горизонтально-проецирующей оси j, проходящей через вершину конической поверхности S (рис. 318 б). Как видим самая большая образующая - S-1- коричневая, самая маленькая S-8 - зелёная.

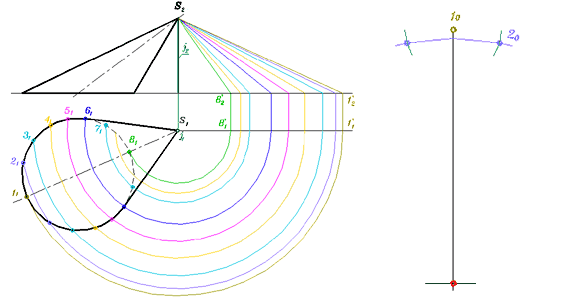
Рис. 318-б

Приступаем к построению самой развёртки. Для этого проведем произвольную вертикальную черту, и на ней отложим отрезок S⁰-1⁰ равный длине самой большой образующей S-1. Из точки S⁰ дугой отложим по обе стороны длину хорды 1₁-2₁. Из точки 1⁰ дугой радиусом S₂-2'₂ зафиксируем на развёртке точки 2⁰ и ей симметричную относительно S⁰-1⁰ (рис. 318 в).

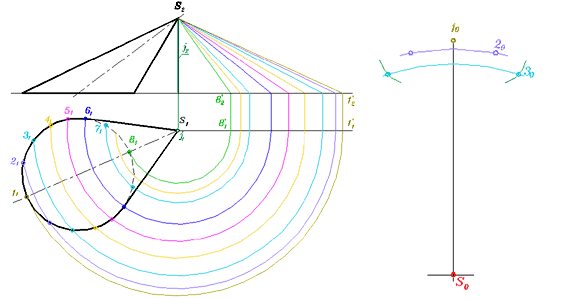
Рис. 318-в

Для построения точки 3⁰ и ей симметричной относительно S⁰-1⁰ измеряем длину хорды 2₁-3₁ и фиксируем её дугами из точки 2⁰ и ей симметричной относительно S⁰-1⁰. Из точки 2⁰ дугой радиусом S₂-3'₂ зафиксируем на развёртке точки 3⁰ и ей симметричную относительно S⁰-1⁰ на предыдущих дугах (рис. 318 г).

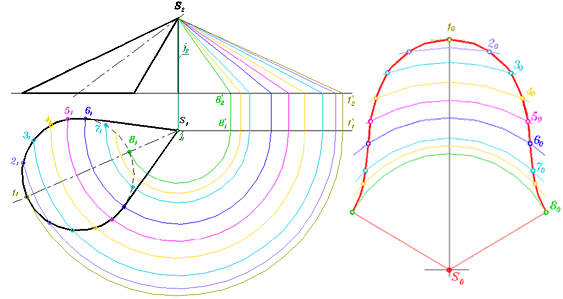
Рис. 318-г

Поступая так многократно закончим построение остальных точек.

Плавной кривой соединяем точки развёртки окружности основания. 8⁰-ю и ей симметричную точку соединяем с точкой S⁰. Это самая маленькая образующая данного конуса, по которой считаем разрезана поверхность конуса.

У плавной кривой, ограничивающей развёртку данного конуса,есть точкаа перегиба. Её положение соответствует точке касания горизонтальных проекций очерковых образующих горизонтальной проекции направляющей. В данном случае это соответствует 6-ой точке.

Построение развёртки мы могли бы начать с самой маленькой образующей. В этом случае развёртка выглядит несколько по иному (рис. 318-д).

Рис. 318-д

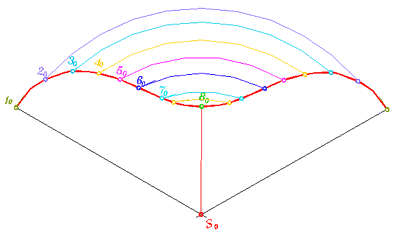
[Содержание] [Первая] [Назад] [Вперед]