|
МЕТРОЛОГИЧЕСКИЕ ОСНОВЫ И МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ОБРАБОТКИ ДАННЫХ ЭКСПЕРИМЕНТА
Планирование эксперимента
Под планированием эксперимента понимается постановка опытов по заранее составленной схеме, обладающей какими-то оптимальными свойствами /5,6/. При этом варьируются все исследуемые факторы одновременно; влияние остальных, в том числе и неизвестных факторов рандомизируется с помощью статических приемов. На всех этапах исследования активно используются математические методы, которые применяются не только для обработки результатов наблюдений, но и при анализе полученных зависимостей, при приятии решения , при формализации априорных данных и т.д.
При планировании эксперимента изучаемого объекта выбирают входные параметры Хi, воздействующие на него и выходные параметры У.
Входные параметры, отвечающие разным способам воздействия на объект, называются факторами и должны удовлетворять следующим требованиям: управляемость; однозначность; независимость факторов; совместимость с другими факторами; точность фиксации факторов должна быть высокой; выбранное множество факторов должно быть полным. Фиксированное значение фактора называется уровнем.
Выходной параметр является реакцией изучаемого объекта (процесса) на воздействие факторов и называется откликом. Если планирование эксперимента решает задачу оптимизации процесса, то в этом случае выходной параметр называется параметром оптимизации. Отклик должен удовлетворять следующим требованиям: быть количественным и выражаться одним числом; эффективным с точки достижения цели; универсальным; имеющим физический смысл; простым и легко вычисляемым; существующим для всех различных состояний.
Задача планирования эксперимента заключается в нахождении некоторой приближенной зависимости математического ожидания параметра оптимизации У от факторов Хi. (функции отклика). В общем случае представление неизвестной функции отклика удобно брать в виде полинома:
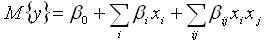 (5) (5)
где βi - коэффициенты регрессии, которые определяются из эксперимента.
Пользуясь результатами эксперимента, можно определить лишь выборочные коэффициенты регрессии b0, bi, bij, которые являются оценками для теоретических коэффициентов регрессии β0, βi, βij.. Тогда уравнение регрессии получаемое на основании результатов эксперимента имеет вид:
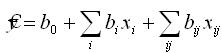 (6) (6)
где 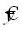 - теоретическая оценка математического ожидания отклика. - теоретическая оценка математического ожидания отклика.
Определив коэффициенты регрессии с помощью метода наименьших квадратов, получим представление о влиянии изучаемых факторов на процесс, о взаимодействии факторов и о направлении движения к оптимальной области.
Эксперимент, реализующий все возможные неповторяющиеся комбинации уровней независимых факторов, каждый из которых варьируется на двух уровнях (обычно на верхнем и нижнем), называется полным факторным экспериментом. Число этих комбинаций равно N=2k , где k – число варьируемых факторов. Полный факторный эксперимент оформляют в виде матрицы планирования (см. табл.,,, примера). При этом вводят следующие обозначения: (+1) – верхний уровень фактора (максимальное значение), (-1) – нижний уровень фактора (минимальное значение), 0 – основной уровень фактора.
С помощью методов регрессионного анализа устанавливают значимость оценки по t-критерию Стьюдента, сравнивая с критическим критерием tкр /8/:
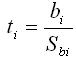 (7) (7)
где 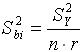 - дисперсия коэффициента регрессии bi; n- число различных вариантов опытов; r- число повторений опыта; - дисперсия коэффициента регрессии bi; n- число различных вариантов опытов; r- число повторений опыта; 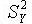 - дисперсия результирующего признака. Критическое значение критерия Стьюдента tкр находят по соответствующим статистическим таблицам при n(r-1) – степени свободы и заданном уровне значимости α. Если ti> tкр, то коэффициент bi признается значимым, в противном случае он статически незначим, т.е. βi =0. Определяют доверительный интервал длиной 2βbi по формуле: - дисперсия результирующего признака. Критическое значение критерия Стьюдента tкр находят по соответствующим статистическим таблицам при n(r-1) – степени свободы и заданном уровне значимости α. Если ti> tкр, то коэффициент bi признается значимым, в противном случае он статически незначим, т.е. βi =0. Определяют доверительный интервал длиной 2βbi по формуле:
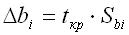 (8) (8)
При этом, следует учесть, что коэффициент регрессии значим, если его абсолютная величина больше половины длины доверительного интервала, иначе этот коэффициент незначим и его можно отбросить.
Необходимо проверить адекватность построенной модели с помощью критерия Фишера, путем выявления соотношения между дисперсией адекватности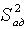 и дисперсии воспроизводимости и дисперсии воспроизводимости 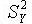 по формулам: по формулам:
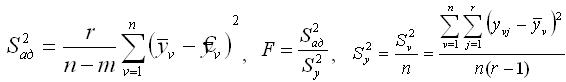 (9) (9)
Критическое значение критерия Фишера Fкр определяют по статистическим таблицам для степеней свободы: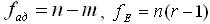 при заданном уровне значимости α. Если F <Fкр, то полученная модель адекватно представляет объект. при заданном уровне значимости α. Если F <Fкр, то полученная модель адекватно представляет объект.
Определение функции отклика с помощью планирования эксперимента состоит из следующих этапов:
1) планирование эксперимента путем построения матрицы планирования, которая задает условия опыта, а так же возможные условия взаимодействия;
2) Собственно эксперимент;
3) Построение математической модели ,связывающий основные факторы и изучаемый параметр. Расчет коэффициентов модели с помощью матрицы планирования.
4) Проверка воспроизводимости (однородности выборочных дисперсий);
5) Проверка статической значимости коэффициентов регрессии.
6) Проверка адекватности математической модели.
Рассмотрим применение планирования эксперимента на примере.
Пример. Разработать математическую модель формовочной смеси с учетом следующих параметров, определяющих ее качество: прочность в сыром виде У1; газопроницаемость У2; влажность У3. /1/. Основными факторами, определяющими качество смеси являются: содержание в ней глины Х1, количество вводимой в смесь влаги Х2; время перемешивания Х3. В качестве математической модели рекомендуется брать полином первой степени вида:
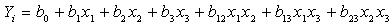
Решение. 1. Задаться основным уровнем шагом варьирования для каждого фактора.
2. Определить верхний и нижний уровень варьирования для каждого фактора. Результат оформить в виде таблицы 2.
Таблица 2
Показатель |
Основные факторы, % |
Глина, Х1 |
Вода, Х2 |
Время, Х3 |
Уровень:
Основной, (0) |
15 |
5 |
7,5 |
Верхний, (+1) |
20 |
5,8 |
10 |
Нижний, (-1) |
10 |
4,2 |
5 |
Шаг варьир. |
5 |
0,8 |
2,5 |
1. Построить матрицу планирования полного факторного эксперимента с учетом эффекта взаимодействия (таблица 3).
Таблица 3
№
опыта |
Основные факторы |
Эф-кт взаимодейст. |
Код
опыта |
Параметры смеси |
Х1 (а) |
Х2 (в) |
Х3 (с) |
Х1,2 |
Х1,3 |
Х23 |
У1 |
У2 |
У3 |
1 |
+ |
+ |
+ |
+ |
+ |
+ |
авс |
1,52 |
92 |
6,38 |
2 |
- |
+ |
+ |
- |
- |
+ |
вс |
0,52 |
163 |
5,48 |
3 |
+ |
- |
+ |
- |
+ |
- |
ас |
0,96 |
110 |
4,76 |
4 |
- |
- |
+ |
+ |
- |
- |
с |
0,68 |
142 |
3,4 |
5 |
+ |
+ |
- |
+ |
- |
- |
ав |
1,16 |
77 |
6,66 |
6 |
- |
+ |
- |
- |
+ |
- |
в |
0,32 |
152 |
5,78 |
7 |
+ |
- |
- |
- |
- |
+ |
а |
0,4 |
105 |
5,12 |
8 |
- |
- |
- |
+ |
+ |
+ |
(1) |
0,28 |
143 |
3,96 |
2. Провести эксперимент и занести результаты реализации плана эксперимента в таблицу 3
3. Записать уравнения (математическую модель) для изучаемых параметров:
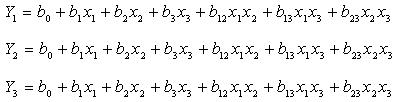
4. Определить с помощью таблицы планирования эксперимента коэффициенты математической модели по формулам:
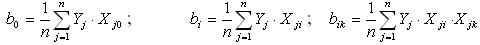
где Yj – изучаемый параметр (см. таблицу); Xij – основной фактор (см. таблицу).
Результаты расчета свести в таблицу 4.
Таблица 4
Параметр
смеси |
Коэффициент регрессии |
b0 |
b1 |
b2 |
b3 |
b12 |
b13 |
b23 |
У1 |
0.73 |
0.28 |
0.15 |
0.19 |
0.18 |
0.04 |
-0.05 |
У2 |
123 |
-27 |
-2 |
3.75 |
-9.5 |
1.25 |
2.75 |
У3 |
5.19 |
0.54 |
0.88 |
-0.19 |
-0.09 |
0.03 |
0.04 |
5. Записать математическую модель:
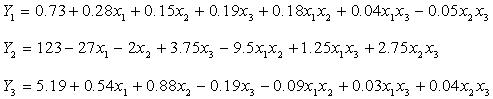
|










