|
МЕТРОЛОГИЧЕСКИЕ ОСНОВЫ И МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ОБРАБОТКИ ДАННЫХ ЭКСПЕРИМЕНТА
Регрессионный анализ.
Корреляционный анализ ставил задачей проанализировать структуру связей между рассматриваемыми переменными и измерить степень их взаимозависимости. После того как исследователь убедится в наличии статистически значимых связей, он приступает к выявлению и математическому описанию конкретного вида интересующих его зависимостей. Надлежащая статистическая обработка данных эксперимента приводит к теоретическому осмыслению результатов и к конечной цели экспериментального анализа – выявлению законов, явлений, позволяющих предсказывать ход интересующих нас процессов, а значит научиться управлять ими и находить оптимальное решение. С этой точки зрения важнейшей задачей анализа эксперимента является установление эмпирических зависимостей для исследуемых процессов. Всякую функцию, приближающую дискретные (табличные) данные, полученные при наблюдениях или эксперименте, называют эмпирической функцией (зависимостью).
Выше указанное и составляет содержимое регрессионного анализа.
Термин ”Regression” (лат.)- «отступление, возврат к чему – либо» связан с прикладной спецификой одного из первых конкретных примеров использования.
Основная задача регрессионного анализа – изучение зависимости между результативным признаком У и наблюдавшимся признаком Х, оценка функции регрессии. При этом:
1) У- независимые случайные величины, имеющие постоянную дисперсию;
2) Х- величины наблюдаемого признака (величина неслучайная).
Регрессионный анализ осуществляется в следующей последовательности:
- выбор и определение функции регрессии;
- проверка гипотезы об общем виде искомой функции;
- анализ содержательной сущности используемой зависимости.
Выбор и определение функции регрессии. Регрессионный анализ начинается с выбора класса функций, в рамках которых предполагается вести поиск наиболее подходящей аппроксимации.
Этап подбора функции регрессии является ключевым, и оттого, насколько удачно он будет реализован, решающим образом зависит точность воспроизведения неизвестной функции регрессии. Этот этап находится в самом невыгодном положении, т.к. не существует стандартных рекомендаций и методов, которые бы образовывали строгую теоретическую базу для этого этапа. Есть некоторые практические рекомендации, которые следует учитывать при решении этой проблемы:
1. Максимальное использование априорной информации о физической сущности аппроксимируемой зависимости.
2. Предварительный анализ геометрической структуры исходных данных.
3. Различные статистические приемы обработки исходных данных, позволяющие сделать выбор из нескольких вариантов.
Пример анализа априорной информации (т.е. до обращения к исходным статистическим данным):
- будет ли искомая функция монотонной или иметь экстремумы (один или более двух);
- следует ли ожидать асимптоты (например, температура нагрева опор по времени)
- какова природа воздействия предикаторных переменных на результат (аддитивная , мультипликативная ) ;
- требуется ли, чтобы график обязательно прошел через заданные точки линейных зависимостей, описывающих эти связи как в парном, так и в многомерном случае.
Определение эмпирической зависимости проходит в несколько стадий:
1 - подбор класса функций, в рамках которого будет вестись дальнейший анализ;
2 – определение (если это необходимо) наиболее информативных предсказываю-щих переменных;
3 - вычисление оценок для неизвестных параметров, участвующих в записи уравнения искомой зависимости;
4 - анализ точности полученного уравнения связи.
Наиболее распространенным в статистической практике являются параметрические регрессионные схемы, когда в качестве класса допустимых решений выбирается некоторое параметрическое семейство функций: линейные, степенные, алгоритмические полиномы.
После выбора вида функции регрессии дальнейшая работа сводится к наилучшему – в смысле выбранного критерия – подбору параметров выбранной функции, а это уже делается с помощью полностью формализованного алгоритма соответствующей оптимизационной задачи – процедуры статистического оценивания.
Рассмотрим несколько результатов эксперимента, когда управляемой переменной X соответствует какой-то отклик Y. Можно вычислить коэффициент корреляции и убедиться, что связь между Х и У есть и что она линейного типа.
Можно попытаться на глаз проложить эту линейную зависимость (рис.1). Чем мы руководствуемся при этом – интуитивно? В общем-то тем, что бы прямая прошла примерно в «гуще» точек, где-то «в середине». Ну а, как всё-таки строго найти правило прокладки прямой? Каков должен быть критерий близости (адекватности) при проведении линии регрессии через множество опытных точек.
Более строго: пусть значение исследуемого результирующего показателя У при данных фиксированных конкретных величинах X(1), X(2)….X(P) случайным образом флуктуирует вокруг некоторого неизвестного уровня описываемого функцией вида F(X(1),X(2),…X(P)).
Тогда Y=F(X(1) ,X(2)…X(P)) + ε(x(1) ,….,x(p)), где остаточная флуктационная компонента ε(x) определяет случайное отклонение значения У от уровня принятой функции F. Флуктуация может быть заложена как в природе процесса, описываемого функцией F, так и случайными ошибками измерения.
Функция F(X(1),X(2),…,X(P)) описывающая зависимость YСР(X) результирующего показателя от заданных фиксированных значений предсказывающих переменных называется функцией регрессии.
Функция F должна быть восстановлена так, чтобы флуктуационная компонента была, возможно, меньше, а для этого необходимо каким-то образом выразить этот флуктуационный остаток как функцию потерь (функция потерь Андрюса, функция Мешалкина, оценка Байеса и др).
Какую из них выбрать? Дело ли это вкуса или есть какие-то научные предпочтения? Если распределение У нормальное во всех сечениях x(i), то самой удачной оценкой функции потерь является функция ρ=∑u2i
Процедура минимизации функции min(ρ)=∑u2i называется методом наименьших квадратов (МНК), основные свойства которого:
- простой и изящный математический аппарат;
- метод приближает F(x) к несмещённой оценке математического ожидания в каждом сечении;
- метод минимизирует дисперсию в каждом сечении, т.е. даёт наименьшую по-грешность оценки прогноза.
Этот метод, разработка которого связана с именами Лежандра и Гаусса, стал очень заметной вехой в математике. С его аппаратом связано появление линейной алгебры (методы решения систем линейных уравнений, вся алгебра матриц и т.д.). Однако метод наименьших квадратов – это аппарат минимизации, и он не отвечает на основной вопрос: какова должна быть функция f(x), т.е. сама модель?
Рассмотрим более подробно этапы регрессионного анализа и применение МНК к определению коэффициентов функций.
I. Этап выбора функции регрессии. Здесь осуществляется выбор семейства функций, в рамках которого производится дальнейший поиск, состоящий в уточнении параметров модели выбранного семейства. Данная стадия регрессионного анализа является наиболее важной и одновременно наименее теоретически обоснованной. Наиболее распространенные вид регрессионной функций - алгебраические полиномы:
y=a0+ ∑aixi+ ∑ ∑aij xi xj+…..
Для переменных, связь которых хорошо подтверждается линейной корреляцией это полином первого порядка:
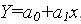
где a0 и a1 могут быть выражены через коэффициент корреляции и статические характеристики.
Для не столь очевидных совокупностей опытных данных следует исследовать полиномы повышающихся степеней, хотя наступает предел, когда повышение степени полинома перестаёт давать эффект. При степени полинома, близкой или равной количеству точек эксперимента интерполяционные свойства полинома делаются абсурдными. Что касается природных процессов, то, как правило, хватает полинома второго порядка. Вообще, контуры листьев, человеческого тела и тел животных и т.д. очерчены кривыми второго порядка.
На базе полиномиальной аппроксимации построено много остроумных вариаций, особенно в части множительной регрессии. Именно для полиномиальной аппроксимации характерно использование всей мощи аппарата линейной алгебры. Для неё этот аппарат и был создан. Изящество этого метода состоит в том, как обильная информация превращается в небольшое количество коэффициентов полинома.
Для определения коэффициентов функции алгебраического полинома можно использовать аппарат метода наименьших квадратов (МНК) и рассмотрим применение его на примере нахождения коэффициентов полинома второго порядка, где надо найти три неизвестных параметра а0, а1, а2:
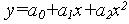
Пусть мы имеем n точек опыта, для которых составляем уравнения в виде полинома второго порядка (функция регрессия):
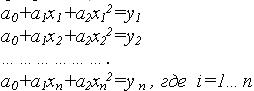
Суть МНК – это минимизация суммы квадратов отклонений (невязок) опытных данных от функции регрессии:
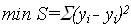
Функция S есть функция трёх переменных (а0, а1, а2) и для достижения её экстремума необходимо что бы её градиент был равен нулю: 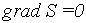
Или по компонентам: 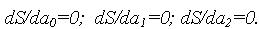
Развернём функцию S: 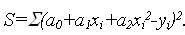
Тогда
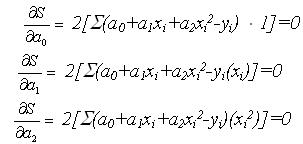
Сокращая на 2 и группируя члены с а0, а1 и а2 получаем:
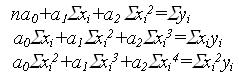
Решение этой системы линейных уравнений позволяет определить коэффициенты полинома а0,а1 и а2, обеспечивающих минимум невязок min S. Таким образом, информация по n точкам отобразилась в информацию по трём коэффициентам.
Вид зависимости (функция регрессии) обычно выбирают исходя из визуальной оценки характера расположения точек на поле корреляции, опыта предыдущих исследований, соображений профессионального характера, основанных на знании физической сущности процесса.
В общем случае зависимость между переменными У и Х выражается полиномом k-й степени:
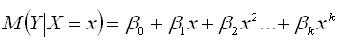 (1) (1)
где βi- коэффициент регрессии.
Если оценки коэффициентов регрессии βi обозначить как bi , то с помощью метода наименьших квадратов их можно найти из системы уравнений:
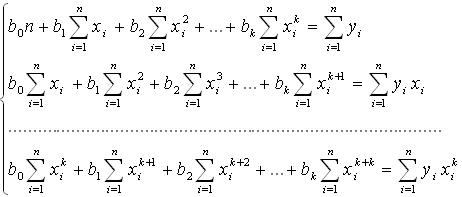 (2) (2)
Для линейной регрессии – уравнение имеет вид: 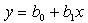 , а коэффициенты регрессии определяются из системы уравнений 2: , а коэффициенты регрессии определяются из системы уравнений 2:
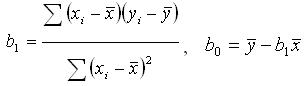 (3) (3)
где 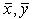 - среднее значение переменной Х и У. - среднее значение переменной Х и У.
Для нелинейной регрессии коэффициенты уравнения также определяются на основе сведения нелинейного уравнения к линейному, например:
1. Экспоненциальная функция 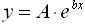 путем логарифмирования сводидтся к линейной путем логарифмирования сводидтся к линейной 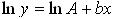 . Тогда с помощью метода наименьших квадратов (МНК), коэффициенты регрессионного уравнения определяются по формуле: . Тогда с помощью метода наименьших квадратов (МНК), коэффициенты регрессионного уравнения определяются по формуле:
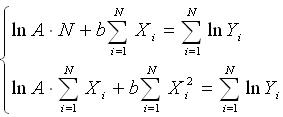
2. Показательная функция у=А*ВX подобным же образом сводится к линейной и тогда коэффициенты регрессионного уравнения можно определить по следующей зависимости:
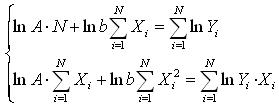
3. Степенная функция у=А*XВ, путем логарифмирования сводится к линейной и тогда с помощью МНК коэффициенты определяются с помощью системы уравнений:
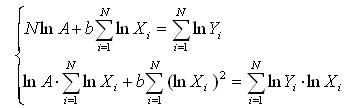
4. Гипербола 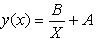 считается частным случаем степенной, поэтому для определения неизвестных параметров используем систему уравнений: считается частным случаем степенной, поэтому для определения неизвестных параметров используем систему уравнений:
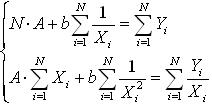
5. Логистическая кривая 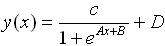 : :
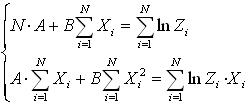 , где , где 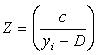
Коэффициенты регрессии обладают следующими свойствами:
1. Чем больше по абсолютному значению величина коэффициента регрессии bi, тем сильнее влияние его на выходной параметр в заданном интервале варьирования переменных.
2. Если bi>0, то увеличение переменной хi вызывает увеличение выходного параметра. При bi<0 увеличение хi приводит к уменьшению критерия оптимизации.
3. Если коэффициент регрессии типа bij значим, то действие переменной хi зависит от уровня, на котором находится другой фактор хj.
4. Вклад слагаемого bij хi хj в величину критерия оптимизации при bij>0 будет положительным, если оба фактора находятся на верхних или нижних уровнях. Вклад будет отрицательным, если факторы находятся на разных уров-нях. При bij<0 картина будет обратной.
Проверка гипотезы об общем виде искомой функции осуществляется с привлечением математико-статистических критериев: оценивается значимость и интервальная оценка коэффициентов регрессии, проводится сравнение дисперсии: дисперсии воспроизводимости процесса и дисперсии адекватности, т.е. рассеяния результатов относительно функции регрессии и т.д.
Анализ содержательной сущности используемой зависимости осуществляется после окончательного определения регрессионной модели и заключается в определении адекватности выбранной модели.
Среди фундаментальных идей, которыми необходимо руководствоваться при проведении регрессионного анализа следует выделить:
- идею компромисса между сложностью регрессионной модели и точностью её оценивания;
- идею поиска модели, наиболее устойчивой к варьированию состава выборочных данных, на основании которых она оценивается;
- идею проверки гипотез об общем виде функций регрессии на базе сравнения выборочных критериев адекватности и исследования статических свойств оценок методов.
|










