МЕТРОЛОГИЧЕСКИЕ ОСНОВЫ И МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ОБРАБОТКИ ДАННЫХ ЭКСПЕРИМЕНТА

        Анализ структуры и тесноты статической связи между исследуемыми переменными. (Корреляционный анализ).

       В исследованиях станков преобладают случаи, когда устанавливается степень зависимости случайного результирующего показателя У от неслучайных переменных Х (например, шероховатости от подачи). Реже устанавливается наличие степени тесноты связи между двумя случайными векторами: результирующим показателем У и предикаторной переменной Z, которая зависит от множества неконтролируемых факторов (например: точность детали от партии заготовки). Подобный анализ называется корреляционным. Оценка степени тесноты связи осуществляется с помощью коэффициента корреляции или корреляционного отношения.
       Условием проведения корреляционного анализа является то, что рассеяние результирующей переменной не должно противоречить нормальному закону распределения. Это требуется предварительно оценить по известным статистическим критериям, например: критерий Пирсона или критерий Смирнова-Мизеса.

       Пусть в эксперименте получены статистические данные, рассеяние которых не противоречит нормальному закону распределения и имеют явно линейную зависимость (рис.2,5):

       Запишем эти данные в виде таблицы.

       Такая таблица называется корреляционной. Для каждой переменной вычисляют:
       - математическое ожидание:

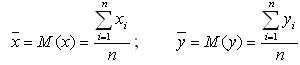
       - выборочную дисперсию:

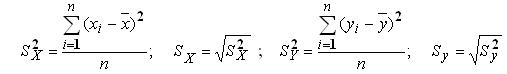
       Тогда теснота связи между переменными Х и У будет определяться выбороч-ным коэффициентом парной корреляции по формуле:

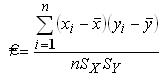
       Коэффициент парной корреляции обладает следующими свойствами:
1. Принимает значения в интервале (-1;+1).
2. Не зависит от выбора начала отсчета и единиц измерения.
3. Является измерителем тесноты только для линейной статистической связи между анализируемыми признаками.
4. Имеет четкий смысл только в случае нормальной распределенности исследуемых случайных величин.
5. Наличие ошибок измерения всегда ослабляет корреляционную связь.
6. Если коэффициент парной корреляции равен 1, то статической зависимости фактически нет - есть функциональная.
7. Если r>0, то это означает, что при увеличении входной переменной Х увеличивается выходная переменная У (рис.1); если r<0 , то при увеличении Х уменьшается У (рис.4); при r=0 переменные Х и У полностью взаимно независимые.
       Математическое ожидание (М(х), М(у)), выборочная дисперсия (SX, SY), коэффициент парной корреляции r, составляют те пять параметров, которые дают исчерпывающие сведения о стохастической зависимости случайных величин Х и У.
       Во всех остальных случаях (распределения Х и У отклоняются от нормального , одна из исследуемых величин не является случайной и т.д.) коэффициент парной корреляции r можно использовать лишь в качестве одной из возможных характеристик тесноты связи. При r=0 исследуемые величины могут оказаться связанными, поэтому в этом случае говорят, что исследуемые величины некоррелированы, и лишь после дополнительного анализа можно говорить об их независимости. Для этого необходимо проверить значимость коэффициента корреляции, т.е. установить достаточна ли его величина для обоснованного вывода об отсутствии корреляционной связи (так называемая нулевая гипотеза: Н₀: r=0). Нулевую гипотезу проверяют по критерию Стьюдента:

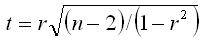
       где n- число степеней свободы. По статистическим таблицам определяют для заданного уровня значимости α и числу степеней свободы n-2 критическое значение критерия Стьюдента (t_кр). Если t_i > t_кр, то коэффициент корреляции признается значимым, в противном случае он статически незначим, т.е. r =0.
       И, наконец, если даже установлена тесная корреляционная зависимость между двумя исследуемыми величинами, из этого непосредственно не следует их причинная взаимообусловленность.

       На практике часто предпосылки корреляционного анализа нарушаются: один из признаков не является случайной величиной, признаки не имеют совместного нормального распределения или зависимость между ними явно нелинейная (рис.3). В этих случаях коэффициент корреляции теряет свой смысл как характеристика степени тесноты связи. Однако, статистическая зависимость между ними может существовать. Для изучения связей между признаками в этом случае существует общий показатель их зависимости – корреляционное отношение, основанное на показателе изменчивости - общей (или полной) дисперсии. Общая дисперсия-это дисперсия случайной величины относительно ее математического ожидания.
       Наиболее привлекательной в этом смысле является ситуация, в которой характер выборочных данных (их количество, «плотность», расположения на плоскости) допускает их группировку по оси выходной переменной У и возможности подсчета средних ординат внутри каждого интервала группирования. Введем следующие обозначения:
- число интервалов группирования k (по оси Х);
- число выборочных точек, попавших в i-тый интервал m_i (i=1,2,…k);
- средняя ордината mi точек в i-том интервале .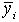
       Найдем дисперсию средних значений в интервалах группирования относительно генерального среднего:

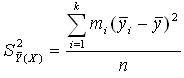       ,       где 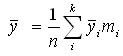- генеральное среднее.

       Общая выборочная дисперсия всех точек относительно генерального среднего:

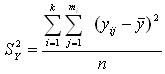
       Отношение дисперсии средних в интервалах 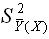к общей выборочной дисперсии около общего среднего :

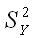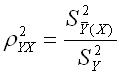
называется корреляционным отношением зависимой переменной У относительно независимой Х.
       Корреляционное отношение обладает следующими свойствами:
1. Корреляционное отношение всегда положительно.
2. ρУХ в общем случае не равно ρХУ.
3. При |ρ|=1 имеет место однозначная функциональная связь между Х и У. Справедливо и обратное отношение.
4. При ρ=0 средние в интервалах yi сохраняют постоянное значение, равное yi. Это значит, что точки эксперимента равномерно располагаются вокруг прямой параллельно оси Х.
5. Корреляционное отношение не может быть меньше абсолютного значения коэффициента корреляции. В случае линейной зависимости эти две характеристики связи совпадают. Это позволяет использовать разность 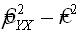как меру отклонения зависимости У=f(Х) от линейного вида.
6. Прочие замечания по поводу коэффициента корреляции и корреляционного отношения совпадают.

       Множественная корреляция. Основные понятия корреляционного анализа, выведенные для парной модели, можно распространить на многомерный случай. Однако для многомерной модели рассмотрение всех возможных парных коэффициентов недостаточно. Здесь необходимо учитывать многообразие связей между переменными, которые отражаются в частных и множественных коэффициентах корреляции. Пусть имеется многомерная нормальная совокупность m с переменными X₁, X₂, X_j, X_m. В этом случае взаимосвязь между переменными можно описать корреляционной матрицей, которая состоит из парных коэффициентов корреляции, вычисляемых по уже знакомой нам формуле с некоторыми особенностями:
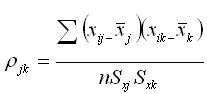, (j,k=1,2,…m), где j , k- порядковые номера признаков.
Сама корреляционная матрица имеет вид:

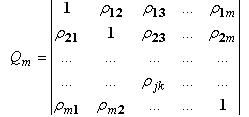
       Однако, одной корреляционной матрицей нельзя полностью описать зависимости между признаками, так как в случае многомерной корреляции зависимости между переменными более многообразны и сложны, чем в двумерном случае. Для этого вводится понятие частных коэффициентов корреляции при фиксируемых n признаках (n-го порядка). Например, можно изучать зависимость между Х₁ и Х₂ при фиксированном Х₃. В этом случае ρ₁₂ есть частный коэффициент корреляции первого порядка. Если зафиксировать все переменные, кроме каких-то двух, то получится частный коэффициент корреляции l-го порядка, где l=m-2.
       Частный коэффициент корреляции может быть легко найден из корреляционной матрицы - из нее вычеркивается все то, что не относится к рассматриваемому частному коэффициенту. Пусть корреляционная матрица из пяти признаков имеет вид:

       Допустим, нам надо найти частный коэффициент корреляции 2-порядка ρ_12-45 – зависимость Х₁ и Х₂ при фиксированных Х₄ и Х₅. Переменная Х₃ не участвует в рассмотрении. Поэтому вычеркиваем 3-ю строку и 3-й столбец. Остается подматрица четвертого порядка.
       В общем виде формула частного коэффициента корреляции l-го порядка имеет вид:

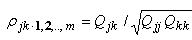
       где Q_jk - алгебраическое дополнение к элементу ρ_jk корреляционной матрицы Qm;
       Q_jj, Q_kk - соответственно алгебраические дополнения к элементам ρ_jj и ρ_кк корреляционной матрицы Q_m.
       Часто представляет интерес оценить связь одного из признаков со всеми остальными. Это можно сделать с помощью множественного коэффициента корреляции:

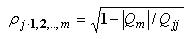
       где - определитель корреляционной матрицы, составленный из выборочных парных коэффициентов корреляции; Q_jj -алгебраическое дополнение к элементу ρ_jj Величина 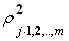называется множественным коэффициентом детерминации.
       Корреляционный анализ позволяет оценить тесноту связи различных переменных друг с другом.