МЕТРОЛОГИЧЕСКИЕ ОСНОВЫ И МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ОБРАБОТКИ ДАННЫХ ЭКСПЕРИМЕНТА

        Математические методы обработки результатов эксперимента. Ошибки измерения. Грубые ошибки.

       Никакое измерение не может быть выполнено абсолютно точно. Его резуль-тат всегда отягощен ошибкой. Измерения, которые были выполнены при градуировке или тарировке наших измерительных инструментов и приборов по сравне-нию с эталонами, также отягощены ошибками. Поэтому измерения с помощью та-ких инструментов нельзя сделать с ошибкой меньшей, чем ошибка присущая самому измерительному устройству.
       Часто стараются произвести измерения с максимально достижимой точностью, т. е. сделать ошибку измерения по возможности малой. Здесь необходимо учесть, что чем точнее мы хотим измерить , тем труднее это сделать. Точность должна быть целесообразной: не надо делать книжную полку, изготовляя доски для нее с точностью до 0,001 мм.
       Вас уже учили, что ошибки измерений делятся на случайные и систематические. Случайные ошибки отражают объективную стохастичность реальных процессов. Систематические ошибки показывают смещение центра рассеяния измеряемой величины во времени ввиду медленно протекающих изменений условий измерения в самом приборе или вне его (температура воздуха, влажности и т.д.).
       В зависимости от способа выражения ошибок, они бывают абсолютные и относительные.
       Вероятностные оценки ошибок основаны на том, что мы воспринимаем каждую реализацию измерения как случайную величину и считаем, что рассеяние измеряемой величины с учетом рассеяния сигнала в измерительном тракте не проти-воречит нормальному закону распределения случайной величины.
       За значение измеряемой величины принимается математическое ожидание, рассчитывается дисперсия и среднеквадратичная ошибка и дается диапазон ожидаемых значений с тем или иным уровнем значимости:

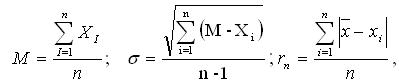
       где n –число измерений; Х_i – результат i-го измерения; М- математическое ожидание; σ -дисперсия; r_n – диапазон ожидаемых значений. В процессе измерения могут возникнуть грубые погрешности или промахи: сбои аппаратуры, ошибки считывания показания прибора человеком и т.д.
       При наличии подозрительных результатов (резко выделяющихся в максимум или минимум) следует, прежде всего, провести непосредственный анализ измерений, тщательную проверку неизменности условий всех экспериментов и т.д. Статистические методы выявления грубых ошибок (критерий Фишера, табличный метод и др.) следует применять лишь в случаях, когда прочие возможные методы определения ошибок исчерпаны. Например, если х₁, х₂,… х_n – взаимно независимые величины (результаты эксперимента), подчиняющиеся нормальному закону, то можно использовать для поиска грубых ошибок в эксперименте статический табличный метод . Для этого определяются отклонения для максимальной величины и минимальной величины, далее по таблицам распределения статистики, по уровню значимости и количеству наблюдений находятся предельные значения отклонений .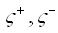
       Итак, мы получили совокупность достоверных статистических данных. Мы заранее должны уяснить для себя, что мы хотим с ними делать, т.е. какова конечная цель статистического исследования зависимости? От этого ответа зависит план дальнейший исследований, выбор общей структуры математической модели, интерпретация получаемых статистических характеристик и т.д. Выделим три основных типа конечных прикладных целей подобных исследований, расположив их по глубине проникновения в содержательную сущность анализируемой задачи:
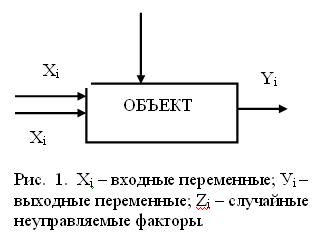
       1. Установление самого факта наличия (или отсутствия) статистической зависимости между входными (управляемыми, регулируемыми) переменными (предикаторами) Х и выходными переменными (отклик) У, характеризующими поведение или результат (эффективность) функционирования (рис.1 )

       2. Прогноз (восстановление) неизвестных значений У исследуемых показателей по заданным значениям Х предикаторных переменных .
       3. Установление функциональной зависимости между исследуемыми признаками; выявление причинных связей между входными переменными Х и результирующими показателями У. Здесь мы уже претендуем на проникновение в физику явлений – в механизм преобразования Х в У.