Лабораторная работа №2

«Метод Форель»

Цель: изучить метод распознавания Форель, определить его особенности и отличия от методов распознавания, основанных на построении гиперплоскости и гиперсферы.

Теория:
Метод "ФОРЕЛЬ" относится к аналитическим методам. В методе используется критерий, оценивающий плотность распределений образов в объеме, ограниченном сферой фиксированного радиуса. При переходе от шага к шагу центр этой сферы движется в сторону увеличения плотности точек – образов (рисунок 3). Сфера стабилизируется в определенном положении, когда плотность точек внутри ее становится максимальной, и любое перемещение сферы ведет к ухудшению ситуации. Точки-образы, попадающие внутрь стабилизировавшейся сферы, образуют класс N1. Процесс повторяется с любой точки из оставшихся и завершается новой стабилизацией сферы, внутри которой находится класс N2 и так далее. Количество классов, получаемых при использовании метода, связано с величиной радиуса сферы.

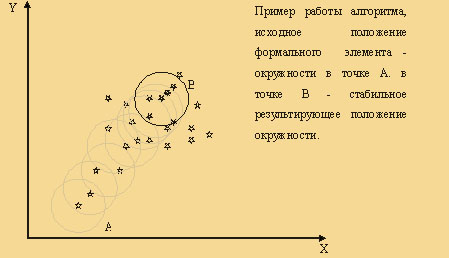
Рисунок 3. Процесс перемещения формального элемента (сферы) по множеству объектов.[5]

Алгоритм. Задается радиус сферы R.

1-й шаг.
Строится сфера радиуса R с центром в любой точке так, чтобы внутрь среды попала хотя бы одна точка - образ Z_I. Определяется центр сферы. Этот центр назовем C⁽¹⁾.

2-й шаг.
Определяются точки - образы ZI⁽¹⁾, для которых | Z_I(1) - CI⁽¹⁾ | <R т.е. эти точки попадают внутрь сферы.

3-й шаг.
Вычисляется центр тяжести таких ZI⁽¹⁾.
Если внутрь сферы попало k точек, то координаты центра тяжести

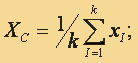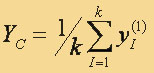
Этот центр тяжести назовем С⁽²⁾

4-й шаг.
Строится сфера радиуса R с центром в точке С⁽²⁾. Определяются точки ZI⁽²⁾, для которых | ZI⁽²⁾ - CI⁽²⁾ | <R.

5-й шаг.
Вычисляется центр тяжести таких ZI⁽²⁾; этот центр тяжести назовем С⁽³⁾ и так далее.
Процесс "движения" среды, т.е. переход от С^(k) к С^(k+1) останавливается тогда, когда расстояние | С^(k) - С^(k+1) | < . Сфера с центром в С^(k+1) представляет собой таксон S1.

6-й шаг.
Точки - образы 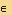S1 из рассмотрения исключаются. В качестве начальной берётся любая точка - образ из оставшихся, и процесс продолжается с шага 1.

7-й шаг.
Последовательность таксонов S1, S2, ...., является последовательностью классов P1, P2, ..., соответствующих радиусу сферы = R.

Задание:

Входные данные:
        • Задается мерность пространства – N (максимальное значение 10).
        • Файл с координатами точек и их номерами (максимальное число точек - 10).

Разработать программное средство, реализующее следующие функции:
        1. считать координаты точек из файла
        2. задать начальную точку для метода «Форель»
        3. предусмотреть возможность задания радиуса пользователем или радиус рассчитывается аналогичным образом, как для гиперсферы в первой лабораторной работе, только нужно реализовать возможность выбор среднего, минимального или максимального расстояния между точками,
        4. выполнить деление точек на классы методом Форель
        5. вывести на экран или в файл номера точек и к какому классу они принадлежат.

Содержание отчета

1. Титульный лист
2. Постановка задачи
3. Графическое описание алгоритма решения задачи (например: в виде блок – схемы)
4. Результаты
        • Вставить скриншот интерфейса программы
        • Рассмотреть работу программы на множестве из 10 точек в двумерном пространстве (изобразить точки на координатной плоскости).
        • Привести результаты разбиения точек на классы.
        • Рассмотреть различные варианты задания радиуса (максимального, среднего и минимального) и заданного пользователем. Привести результаты и сравнить их.
5. Фрагменты кода