Лабораторная работа №1
«Методы распознавания образов, основанные на построении разделяющей гиперплоскости и гиперсферы»
Цель: изучить методы распознавания образов, основанные на построении разделяющей гиперплоскости и гиперсферы.
Теория:
Построение разделяющей гиперплоскости используется для определения принадлежности объекта к тому или иному классу образов. Рассмотрим этапы построения разделяющей гиперплоскости.
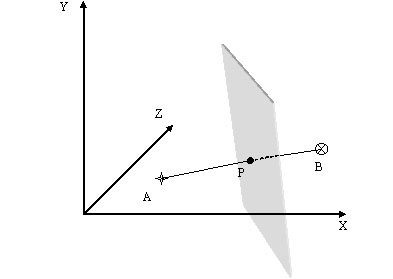
Рисунок 1. Построение разделяющей гиперплоскости.
На рисунке 1 схематически изображен процесс построения разделяющей гиперплоскости. Нам известны координаты двух точек(объектов): A,B. Которые представлены на рисунке в виде звездочки (точка А), и в виде кружочка (точка В). Необходимо построить разделяющую гиперплоскость, которая отделяла бы образы «похожие» на А, от образов «похожих» на В.
Для построения, нам необходимо провести между точками А и В, соединяющую их линию. На середине этой линии отложим точку Р, через которую будет проходить разделяющая гиперплоскость. Теперь, зная координаты точки Р, а также имея вектор АВ, построить плоскость, проходящую через точку Р, и перпендикулярную вектору АВ. Теперь чтобы принять решение о принадлежности образа к тому или иному классу, нужно определить расстояние от этого образа до гиперплоскости, кроме того, знак полученного расстояния будет говорить о положении образа с одной или другой стороны от гиперплоскости.
Разделяющая гиперплоскость не может быть построена без базисных точек. В качестве базисных точек могут быть выбраны:
- наугад взятые точки , по одной из множества А и множества В;
- точки, выбранные из А и В с учетом определенных обстоятельств (например, имеющие минимальные расстояния между собой);
- точки, выбранные на основании каких-либо статистических характеристик.
Пусть нам даны множества А и В, каждое из которых состоит из 5 элементов (рисунок 2):
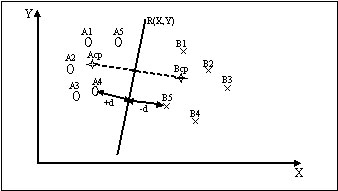
Рисунок 2. Разделение классов А и В гиперплоскостью
В качестве базисных точек выберем точки, координаты которых являются средними арифметическими значениями соответствующие координат точек каждого класса.
В качестве разделяющей классы А и В гиперплоскости выберем следующую плоскость:
R(х,у) = 2(Асред- Всред) * Р + | Bсред |2 - |Aсред|2 = 0, это векторное уравнение
Отметим, что все расстояния точек Ai от гиперплоскости отрицательны:
Все расстояния точек Вi от разделяющей гиперплоскости положительны
Следовательно, R(x,y) разделяет множества А и В и если добавить новый элемент в В, то такое расстояние будет положительно.
Метод гиперсфера аналогичен методу построения гиперплоскости, только разделение заключается в следующем: точки которые попадают внутрь гиперсферы относятся к одному классу, а за ее пределы – ко второму.
Гиперсфера описывается следующей формулой:
(x1 - O1)2 + (x2 - O2)2 + ... + (xn - On)2 = R2, где (О1, О2, …,Оn) – координаты центра сферы, R – радиус гиперсферы, (Х1, Х2, …,Хn) – координаты точки.
Для определения, куда попала точка с координатами (Х1, Х2, …,Хn) в сферу или за ее пределы, преобразуем формулу к следующему виду:
(x1 - O1)2 + (x2 - O2)2 + ... + (xn - On)2 - R2 = 0
Если в результате вычисления формулы получается отрицательное значение, то точка попадает в сферу, если равно нулю – на границу сферы, иначе – за ее пределы.
Задание:
Входные данные:
• Задается мерность пространства – N (максимальное значение 10).
• Файл с координатами точек и их номерами (максимальное число точек - 10).
Разработать программное средство, реализующее следующие функции:
1. считать номера и координаты точек из файла
2. возможность выбора метода распознавания: гиперплоскость или гиперсфера.
Для гиперплоскости:
• выбрать две базовые точки. Предусмотреть следующие варианты выбора: случайным образом, должны задаваться пользователем и выбрать две точки с наименьшим расстоянием между собой из всех возможных вариантов (нужно рассмотреть все возможные пары точек и определить расстояние между ними по формуле
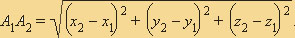
• разбить точки на два класса;
• вывести на экран или в файл: номера точек и в какой класс они попали;
• для каждого класса найти координаты средней точки в каждом классе по следующей формуле:
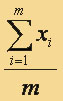
где xi – i – координата каждой точки в классе, m – количество точек в классе.
• далее строим гиперплоскость, в которой в качестве базовых точек берутся средние точки каждого класса. Производим разделение всех точек на основе построенной гиперплоскости.
• Сравнить результаты деления на классы после первого построения гиперплоскости и после второго.
Для гиперсферы:
• выбрать центр гиперсферы. Предусмотреть следующие варианты: случайном образом из множества точек или задается номер точки пользователем
• радиус сферы должен вычисляться двумя способами: задается пользователем или вычисляется следующим образом:
• находим расстояния Ri между центром гиперсферы и с каждой из оставшихся точек по формуле 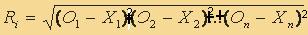 , где (О1, О2, …,Оn) – координаты центра сферы, а (Х1, Х2, …,Хn) – координаты точки.
• находим среднее расстояние 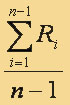 , где n – общее количество точек. Это среднее расстояние и будет радиусом.
• Строим гиперсферу и производим разделение всех точек на два класса.
• Вывести на экран или в файл: номера точек и в какой класс попали.
Содержание отчета
1. Титульный лист
2. Постановка задачи
3. Графическое описание алгоритма решения задачи (например: в виде блок – схемы)
4. Результаты
a. Вставить скриншот интерфейса программы
b. Рассмотреть работу программы на множестве из 10 точек в двумерном пространстве (изобразить точки на координатной плоскости).
c. Привести результаты разбиения точек после двух построений гиперплоскости и гиперсферы.
d. Рассмотреть различные варианты задания базовых точек и вычисления радиуса гиперсферы.
e. Привести результаты и сравнить их.
5. Фрагменты кода
Примечание
Точки обязательно нумеровать цифрами или буквами.
|
