Предположим, деталь в условиях эксплуатации при симметричном цикле нагружения с амплитудой проработала циклов. Согласно рисунку 5.1 запас усталостной прочности по числу циклов можно охарактеризовать отношение , где N₁ – число циклов, соответствующее разрушению детали, т.к точка 1 находится на кривой усталости. Условие прочности при этом можно записать в следующем виде: /N₁ 1.

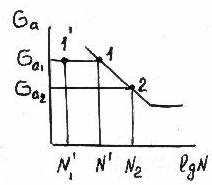
Рис. 5.1 Диаграмма выносливости

Если деталь в условиях эксплуатации отработала циклов с напряжением , а затем циклов с напряжением , то запас прочности можно представить как:

(5.1)

При большом количестве режимов нагружения условие прочности будет иметь вид:

(5.2)

Если теперь из уравнения кривой усталости (3.2) найти число циклов до разрушения и подставить его в (5.2), то получим:

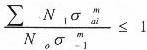(5.3)

Численность этого выражения умножим и разделим на N₀ – суммарное число циклов до разрушения детали, которое называется ресурсом детали. В общем случае под ресурсом понимается время работы детали до выхода из строя (в нашем случае до установленного разрушения). Отношение N_i / N₀ = P_c, назовём вероятностью работы детали с амплитудой напряжений , тогда формула (5.3) будет иметь вид:

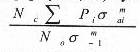= 1 (5.4)

Из этой формулы можно определить ресурс детали:

(5.5)

Мы получили, таким образом, формулу для расчёта ресурса детали, выраженного в числах циклов нагружения, нагруженной переменными нагрузками с различными амплитудами. Если воспользоваться теперь результатами статистической обработки графиков случайного нагружения (см. параграф 2), то знаменатель формулы (5.5) можно вычислить, зная параметры блока погружения, как показано на рисунке 2.2 и полагая, что N_c = λ * N₆, где λ – число блоков нагружения; N₆ – число циклов нагрузки в блоке (за километр пробега, сезон работы и т.д.).

Теперь можно найти ресурс, выраженный в числе блоков нагружения:

(5.6)

Как мы установили, характеристики сопротивления усталости и режимы погружения являются случайными величинами и для каждой детали рассматриваемой партии будут различными. Очевидно, что нас интересует такой ресурс, при котором не будет происходить усталостных разрушений, или эти разрушения сводятся к минимуму (например, разрушится 5% от всей партии деталей).

Многочисленные эксперименты и опыт эксплуатации показывает, что ресурс деталей при усталостных разрушениях, как случайная величина, имеет логарифмически нормальное распределение со средним значением:

(5.7)

и средним квадратичным отклонением логарифма ресурса:

, (5.8)

где - среднее значение амплитуды каждой ступени блока нагружения;

- коэффициенты вариации предела выносливости и амплитуд напряжений в блоке нагружения.

По формулам (5.7) и (5.8) можно построить график функции распределения ресурса по формуле:

, (5.9)

где U_p – квантиль нормального распределения, находится по таблицам математической статистики в зависимости от задаваемой вероятности разрушения P / 5 /.

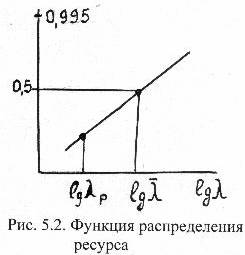
На рисунке 5.2 показан такой график, построенный / 6, стр.211 – 219 /.

< В начало >

< Содержание >