Глава 2. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ

ПОПЕРЕЧНЫХ СЕЧЕНИЙ БРУСА

При расчете бруса на растяжение-сжатие необходимо знать площадь его поперечного сечения, в расчетах на изгиб и кручение – более сложные геометрические характеристики.

2.1. Статические моменты площади, осевые, центробежные

и полярные моменты инерции. Их свойства

Для произвольной фигуры (рис. 2.1,а) площадью F, в пределах которой выделена элементарная площадка dF с координатами x, y и , геометрические характеристики можно классифицировать следующим образом:

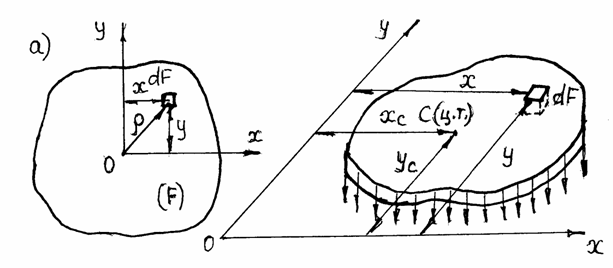
Рис. 2.1. Геометрические характеристики и центр тяжести плоского сечения

Статические моменты площади (используются для определения положения центра тяжести)

, , (м³); (2.1)

Осевые (экваториальные) моменты инерции (используются в расчетах на изгиб)

, , (м⁴); (2.2)

, (м⁴); (2.3)

Полярный момент инерции

, (м⁴); (2.4)

Радиусы инерции

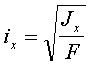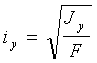, , (м); (2.5)

Их основные свойства:

J_x, J_y, J_p - величины всегда положительные,

S_x, S_y, J_xy - могут быть положительными, отрицательными и равными нулю.

Геометрические характеристики сечения относительно каких-либо осей равны сумме соответствующих величин всех ее частей относительно тех же осей.

Из рис. 2.1,а видно, что r²=x²+y² и J_r=ò_F(x²+y²)dF=ò_Fx²dF+ò_Fy²dF . Учитывая (2.2.), получим

J_r = J_y + J_{x .} (2.6)

2.2. Центр тяжести сечения

Для пластины постоянной толщины (рис. 2.1,б), силу тяжести которой примем равной площади сечения F, интегралы (2.1) можно рассматривать как суммы моментов сил тяжести относительно осей х, у, которые по теореме Вариньона о моменте равнодействующей можно записать:

S_x = ò_F y dF = y_c F; S_y = ò_F x dF = x_с F (2.7)

Отсюда найдем координаты центра тяжести сечения

, , (2.8)

а для сложной фигуры, которую можно разбить на простые

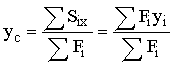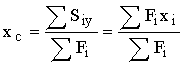, , (2.9)

где F_i, y_i, х_i - площадь и координаты центра тяжести простой фигуры.

Оси, проходящие через центр тяжести сечения, называются центральными. Относительно любых центральных осей статические моменты площади сечения равны нулю (в этом случае в формулах (2.7) y_c =0, х_с=0).

Центр тяжести фигуры, имеющей ось симметрии, находится на этой оси.

ПРИМЕР 2.1. Найти положение центра тяжести (рис.2.2).

РЕШЕНИЕ:

Центр тяжести полукруга находится на оси симметрии «у». Выделим элементарную площадку dF, с помощью двух полуокружностей радиусами r и r+dr, а также с помощью двух лучей, наклоненных к оси х под углами j и dj. Статический момент площади относительно оси х , где , , , тогда 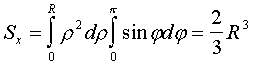, или , т.е. .

Отсюда

. (2.10)

2.3. Зависимость между моментами инерции,

относительно параллельных прямых

Пусть известны моменты инерции фигуры относительно осей х, у (рис.2.3). Требуется определить моменты инерции относительно осей х₁, у₁, параллельных осям х, у. Координаты любой точки в новой системе координат х₂оу₁ можно вычислить через координаты в старых осях. х₂=х+b; у₁=у+а.

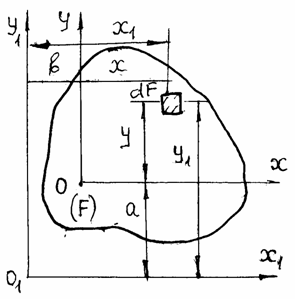
Рис.2.3. Моменты инерции для параллельных осей

Подставляя эти значения в формулы (2.2) и (2.3), раскрываем скобки и, интегрируя почленно, получаем

Jх₁ = ò_F у₁² dF = ò_F (у + а)² dF = ò_F y² dF +а² ò_F dF +2а ò_F y dF,

Jу₁ = ò_F х₁² dF = ò_F (х + b)² dF = ò_F х² dF +b² ò_F dF +2b ò_F х dF,

Jх₁у₁ = ò_F х₁у₁ dF=ò_F(х + b)(у + а) dF= ò_F хуdF +аb ò_F хdF +аòхdF +bò_F уdF,

Учитывая формулы (2.1), (2.2) и (2.3), можно записать

J_x1 = J_x + а²F + 2 а S_x,

J_у1 = J_у + b²F + 2 b S_у, (2.11)

J_х1у1 =J_ху + аbF +а S_у + bS_x,

Если оси х и у - центральные, то S_х = 0 и S_у = 0. Тогда получим формулы перехода от центральных осей х,у к нецентральным х₁, у₁

J_x1 = J_x + а²F,

J_у1 = J_у + b²F, (2.12)

J_х1у1 =J_ху + аbF.

При переходе от осей нецентральных х₁, у₁ к центральным формулы (2.12) примут вид

J_x1 = J_x - а²F,

J_у1 = J_у – b²F, (2.13)

J_х1у1 =J_ху - аbF.

Из формул (2.12) и (2.13) видно, что их всех моментов инерции относительно ряда параллельных осей центральные моменты инерции всегда будут наименьшими.

2.4. Моменты инерции простейших фигур

Рассмотрим параллелограмм и прямоугольник (рис. 2.4).

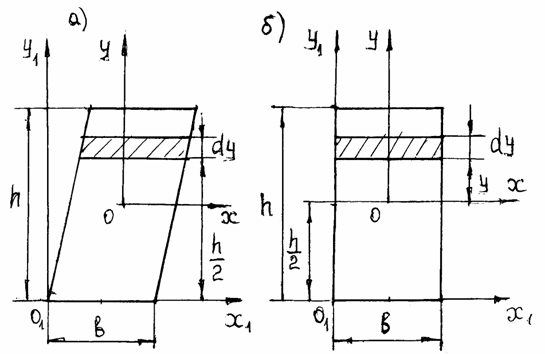
Рис.2.4. Моменты инерции для параллелограмма и прямоугольника

Для рассматриваемых фигур (см. рис.2.4, а, б) dF=bdy

,

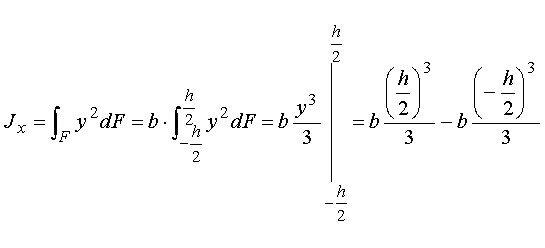или

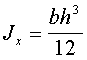. (2.14)

Для прямоугольника:

, (2.15)

Пользуясь формулами перехода от центральных осей к нецентральным (2.12), найдем

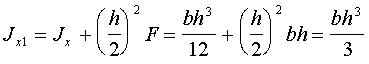. (2.16)

Аналогично (для прямоугольника)

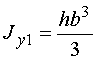. (2.17)

Рассмотрим треугольник (рис.2.5). Здесь dF=b(y)dy. При этом . Следовательно,

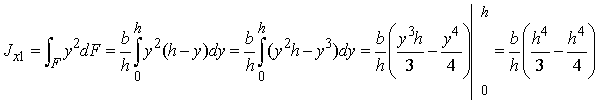
Произведя вычисления, получим

. (2.18)

Относительно оси х, проходящей через центр тяжести треугольника

, или (2.19)

Рассмотрим круг (рис. 2.6). В этом случае .

Полярный момент инерции:

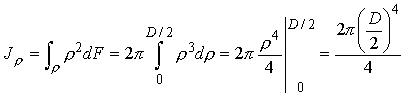, или 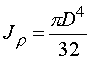(2.20)

Моменты инерции круга относительно осей х, у легко найти на основании выражения (2.6) J_r=J_y+J_x. В силу симметрии круга J_x=J_y, следовательно

J_x=J_y= J_r, или J_x=J_y= . (2.21)

Рассмотрим полукруг (рис. 2.7), центр тяжести которого находится в точке О. Момент инерции полукруга относительно диаметральной оси у₁

. (2.22).

Момент инерции полукруга относительно оси «у» можно определить, пользуясь формулами перехода от нецентральных осей к центральным (2.13).

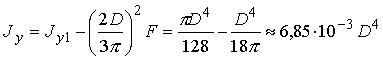. (2.23).

Рассмотрим кольцо (рис.2.8). Полярный момент инерции

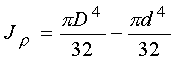, или , (2.24)

где .

Осевые моменты инерции

, или 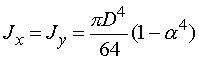. (2.25)

2.5. Зависимости между моментами инерции

при повороте координатных осей

Пусть известны моменты инерции фигуры относительно координатных осей х, у (рис. 2.9) J_x, J_y, J_xy.

Повернем оси х, у на угол «a» против часовой стрелки, считая угол поворота осей в этом направлении положительным. Найдем теперь моменты инерции сечения относительно повернутых осей х₁, у₁. Координаты произвольной площадки dF в новых осях (х₁, у₁) выражаются через координаты х, у прежней системы следующим образом:

; (2.26)

Подставим эти значения в выражения для момента инерции и проинтегрируем почленно.

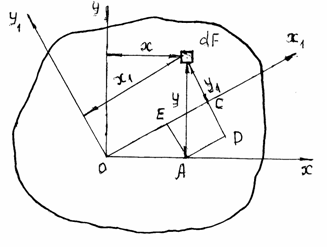
Рис.2.9. Моменты инерции при повороте осей

;

;

,

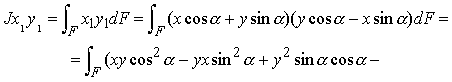
или учитывая (2.2) и (2.3), получим:

, (2.27)

, (2.28)

, (2.29)

Складывая почленно выражения (2.27) и (2.28) и учитывая (2.6), получим:

, (2.30)

т.е. при повороте осей сумма моментов инерции не изменяется и равна полярному моменту относительно начала координат.

При повороте осей на угол a=90⁰

Jx₁=Jy; Jy₁=Jx; Jx₁y₁=-Jxy.

2.6. Главные оси инерции. Главные моменты инерции

Исследуем функцию моментов инерции Jx₁ (2.27) на экстремум:

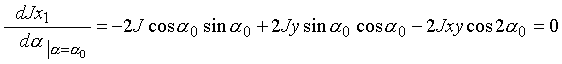
или

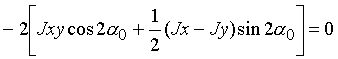(2.31)

т.е. (с учетом (2.29))

или . (2.32)

Таким образом, для осей, относительно которых осевые моменты инерции принимают экстремальные (max и min) значения, центробежный момент инерции равен нулю. Такие оси называются главными.

Итак, оси, относительно которых центробежный момент инерции равен нулю, а осевые моменты инерции принимают экстремальные значения называются главными осями. Осевые моменты инерции относительно главных осей называются главными моментами инерции.

Если главные оси проходят через центр тяжести сечения, то такие оси называются главными центральными осями, а осевые моменты инерции относительно этих осей - главными центральными моментами инерции.

Из уравнения (2.31) получаем формулу для определения направления главных осей инерции U, V (рис. 2.10).

. (2.33)

Значения главных моментов инерции можно получить из формул (2.27) и (2.28), приняв a=a_0.

(2.34)

(2.35)

учитывая, что

, ,

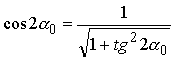а также формулу (2.33), получим для главных моментов инерции:

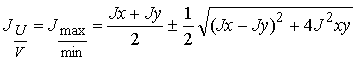. (2.36)

Если сечение имеет ось симметрии (рис. 2.11), то центробежный момент инерции правой половины равен центробежному моменту инерции левой половины . (см. рис.2.11), но с противоположным знаком.

Следовательно, для всей фигуры и оси «х» и «у» являются главными осями. Таким образом, ось симметрии и любая ей перпендикулярная ось являются главными осями.

ПРИМЕР 2.2. Определить главные центральные моменты инерции сечения (рис. 2.12).

РЕШЕНИЕ:

Центр тяжести сечения находится на оси симметрии «у». Центры тяжести элементов фигуры О₁ и О₂ (полукруга и прямоугольника) показаны на рисунке (рис. 2.12). Проведем предварительные оси х и у.

Координаты центров тяжести фигуры в выбранных осях х₁=0; , х₂=0; у₂=0.

Площади элементов фигур: ; .

Координаты центра тяжести «С» всего сечения в осях «х» и «у» : х_с=0,

.

Проведем центральные оси х_с и у_с (см. рис.2.12). Эти оси будут главными центральными осями всего сечения, так как ось у_с - является осью симметрии сечения. Определим момент инерции элементов сечения относительно собственных центральных осей. Для полукруга:

; .

Для треугольника:

Главные центральные моменты инерции:

.

.

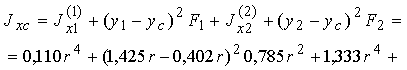
ПРИМЕР 2.3. Определить главные центральные моменты инерции уголка (рис. 2.13).

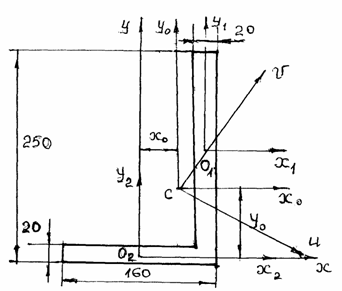
Рис.2.13. Моменты инерции уголка

РЕШЕНИЕ:

Разбиваем уголок на 2 прямоугольника (см. рис. 2.13). Проведем предварительные оси х, у через центр тяжести второго элемента фигуры О₂.

Координаты центра тяжести:

мм;

мм.

Проведем через центр тяжести С центральные оси х_с, у_с. С помощью формул (2.12) получим:

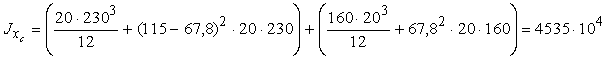мм⁴

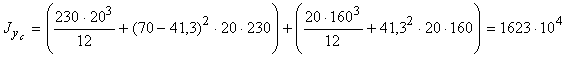мм⁴

мм⁴.

По формуле (2.33) определяем угол наклона главных осей U,V к осям х_с, у_с.

Проведем оси U,V, поворачивая оси х_с, у_с на угол a₀= -22⁰34^/ (по часовой стрелке).

Главные центральные моменты инерции определяются по формуле (2.36):

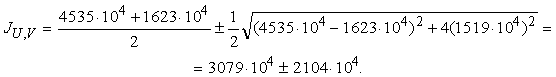
Следовательно: J_U=5183 мм⁴; J_V=975×10⁴ мм⁴.

2.7. Контрольные вопросы к главе 2

2.7.1. Что такое статические моменты площади, осевые, центральный и полярный моменты инерции, радиусы инерции и в каких единицах они измеряются? Чему равен статический момент площади относительно центральной оси? Чему равна сумма осевых моментов инерции сечения относительно двух взаимно-перпендикулярных осей?

2.7.2. Как определяются координаты центра тяжести простых и сложных сечений? Как отражаются на знаке центробежного момента инерции сечения изменения положительных направлений одной или обеих координатных осей? Что такое главные и главные центральные моменты инерции? В каких случаях можно без вычисления установить положение главных осей.

2.7.3. Выведите формулы для определения осевых моментов инерции прямоугольника относительно оси, совпадающей с одной из его сторон и относительно центральной оси, параллельной одной из его сторон.

2.7.4. Выведите формулы для определения осевых моментов инерции треугольника, относительно оси, проходящей через основание и относительно центральной оси, параллельной основанию.

2.7.5. Выведите формулу для определения осевого и полярного моментов инерции для круга и кольца.

2.7.6. Выведите формулу зависимости между осевыми и центральными моментами инерции сечения для параллельных осей. Относительно каких из параллельных осей осевые моменты инерции принимают наименьшее значение?

2.7.7. Выведите формулы, выражающие изменение осевых и центральных моментов инерции при повороте осей.

2.7.8. Выведите формулы для определения положения главных осей инерции и величин главных моментов инерции.

< В начало >

< Содержание >