Глава 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ

1.1.Основная задача сопротивления материалов

Основной задачей сопротивления материалов является определение минимальных размеров деталей сооружений и машин, обеспечивающих их необходимые прочность, жесткость и устойчивость.

При этом подразумевается, что:

прочность - способность твердого тела выдерживать проложенную нагрузку, не разрушались и, как правило, не получая остаточных деформаций;

жесткость - способность элемента конструкции воспринимать нагрузку без возникновения недопустимо больших деформаций;

устойчивость - свойство системы сохранять свое первоначальное состояние под действием внешней нагрузки. Так, например, прямолинейный стержень под действием центрально приложенной силы Р ( рис. 1.1) может изогнуться, т.е. потерять устойчивость прямолинейной формы равновесия.

Сопротивление материалов является одним из разделов механики, а именно, механики деформируемых твердых тел и опирается на основные положения теоретической механики, физики, материаловедения и др.

Основная задача сопротивления материалов решается путем введения упрощающих гипотез, позволяющих получить сравнительно простые расчетные формулы и алгоритмы, которые проверяются и дополняются экспериментальными исследованиями, а также методами теории упругости, рассматривающей аналогичные задачи в более точной постановке. На общих положениях сопротивления материалов основываются другие разделы науки о прочности, такие как детали машин, строительная механика сооружений, самолета, корабля; теория прочности сварных конструкций и т.д. Сопротивление материалов является составной частью науки о прочности, которая ведет свое начало еще со времен Галилея, бурно развивалась и пополнялась новыми знаниями, разделами и направлениями.

1.2. Реальный объект и расчетная схема

Каждый инженерный расчет начинается с идеализации исследуемого объекта. На этом этапе рассматривается реальная конструкция и выделяются те ее особенности, которые являются наиболее существенными.

Реальный объект, освобожденный от несущественных особенностей, называется расчетной схемой.

Так, например, при расчете канатов лифта учитывается вес лифта с грузом, инерционные силы, вес канатов, а нагрузки от аэродинамического сопротивления, измерения барометрического давления при подъеме лифта, как несущественные, не учитываются.

1.3. Основные гипотезы о материале.

Выбор расчетной схемы начинается со схематизации свойств материала путем введения ряда гипотез.

Гипотеза сплошности материала: материал полностью и равномерно, заполняет объем тела. Наличие пустот, трещин, атомистическая структура материала во внимание не принимаются.

Гипотеза об однородности и изотропности: материал имеет одинаковые свойства во всех точках тела и по всем направлениям. Металлы, стекло, смолы считаются изотропными, а дерево, бумага, ткани и т.д. являются анизотропными, т.е. имеют различные свойства по различным направлениям.

Гипотеза об идеальной упругости: в известных пределах нагружения, многие материалы считаются идеально упругими, так как после снятия нагрузки деформации в них практически исчезают.

1.4. Формы элементов конструкции

Элементы реальных конструкций имеют самую разнообразную форму, но каждый из них можно рассматривать либо как брус (рис. 1.2,а), либо оболочку (рис. 1.2,б), или пластину (рис. 1.2,в), либо как массив (рис. 1.2,г).

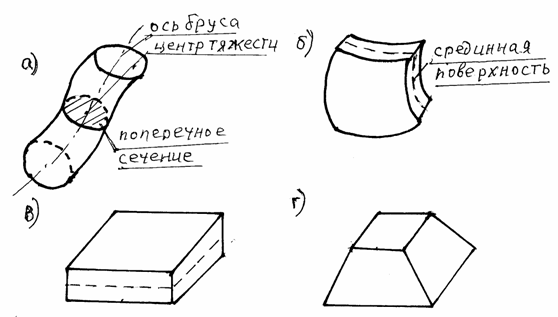
Рис. 1.2. Формы элементов конструкций

Брусом называется тело (рис.1.2,а), одно из размеров которого (длина) намного больше других. Его можно представить как тело, полученное движением плоской фигуры (поперечного сечения бруса), центр тяжести которой перемещается вдоль оси бруса.

Оболочкой называется тело (рис.1.2,б), одни из размеров которого (толщина) намного меньше других.

Поверхность, проходящая посредине толщины, называется срединной поверхностью.

Пластиной называется оболочка (рис.1.2,в), у которой срединная поверхность является плоскостью.

Массивом называется тело (рис.1.2,г), у которого размеры во всех направлениях одного порядка.

1.5. Опорные устройства и опорные реакции

Опорные устройства классифицируются по числу связей, накладываемых на перемещения опорных точек (узлов) тела.

Шарнирно-неподвижная опора (рис. 1.3,а) накладывает две связи и имеет две реакции этих связей Z_А и У_А.

Шарнирно-подвижная опора (рис. 1.3,б) накладывает одну связь и имеет одну реакцию У_А.

В жесткой заделке (трехсвязная опора) ( рис. 1.3,в) возникают три реакции Z_А, У_А и М_А.

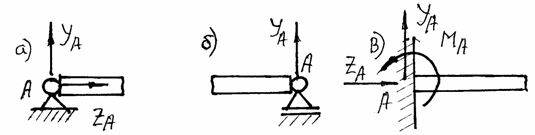
Рис.1.3. Типы опор

1.6. Внешние силы

Внешние силы могут быть объемными (собственный вес, центробежные силы и т.д.) и поверхностными (давление тел друг на друга, давление снега, ветра, воды и т.д.). Характеризуются они интенсивностью нагрузки, измеряются для объемных нагрузок в ^н/_м³, для поверхностных в ^н/_м²,

Если площадь распределения поверхностной нагрузки мала по сравнению с размерами тела, ее заменяют сосредоточенной силой Р, приложенной в точке ( рис. 1.4,а). Измеряется сосредоточенная сила в Н. В ряде случаев внешняя нагрузка может быть приведена к сосредоточенной паре сил (моменту) М (рис. 1.4,б) и измеряется в Н×м. Иногда внешняя нагрузка приводится к распределенной по длине (рис. 1.4,в), интенсивность которой «q» измеряется в ^н/_м.

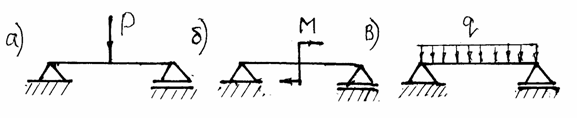
Рис.1.4. Типы нагрузок

По характеру изменения во времени нагрузки могут быть статическими, медленно возрастающими от нуля до конечного значения. Ускорения частиц материала и инерционные силы при этом будут настолько малы, что ими в расчетах можно пренебречь. Динамические нагрузки, быстро изменяются во времени и вызывают значительные ускорения частиц материала и сил инерции, которые необходимо учитывать в расчетах (например, ударные нагрузки).

Повторно-переменные – это нагрузки, которые многократно изменяются во времени по какому-либо закону.

1.7. Внутренние силы. Метод сечений.

Внутренние силовые факторы. Виды нагружений

Под действием внешней нагрузки в нагруженном теле возникают силы взаимодействия между отдельными частями тела, которые называются внутренними силами. При достижении определенного уровня (величины сил сцепления между частицами материала) внутренние силы могут вызвать разрушение материала.

Для определения внутренних сил используется метод сечений, сущность которого заключается в следующем.

Рассекаем нагруженное уравновешенными силами тело на две части сечением I-I, в котором необходимо определить внутренние силы ( рис. 1.5,а)

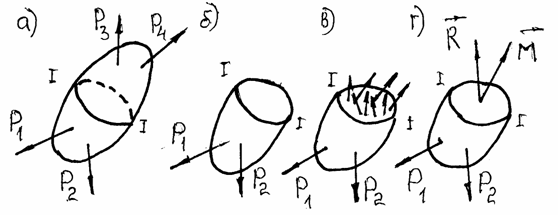
Отбрасываем одну часть тела (рис. 1.5,б).

Заменяем действие отброшенной части внутренними силами, приложенными в сечении I-I ( рис. 1.5,в).

Уравновешиваем оставленную часть, составляя уравнения равновесия. В результате получим главный вектор и главный момент системы внутренних сил (рис. 1.5,г), приложенных в центре тяжести сечения.

Выбираем систему координат x, y, z (рис. 1.6). Раскладывая главный вектор и главный момент на оси x, y и z, получаем шесть составляющих;

N- продольная (нормальная) сила;

Q_x, Q_y - поперечные (перерезывающие) силы;

М_Х, М_У - изгибающие моменты;

М_К - крутящий момент.

Эти шесть составляющих называются внутренними силовыми факторами, которые могут быть определены из шести уравнений равновесия, составленных для оставленной части тела.

Те или иные внутренние силовые факторы возникают при определенных видах нагружения. В частности: при кручении возникают крутящие моменты М_к, при растяжении (сжатии) возникают продольные силы N; при чистом изгибе возникают изгибающие моменты М_х и М_у; при поперечном изгибе, кроме изгибающих моментов, возникают поперечные силы Q_х и Q_у; при сдвиге (срезе) возникают поперечные силы.

Многие детали машин и элементы конструкций работают в условиях одновременного воздействия различных видов нагружения (например: изгиб с кручением, растяжение с изгибом и т.д.).

1.8. Напряжения. Понятие о напряженном состоянии

Мерой внутренних сил является интенсивность их распределения, которая называется напряжением.

Пусть DR - равнодействующая внутренних сил, возникающих на малой площадке DF, выделенной в окрестности точки А поверхности сечения (рис.1.7).

Уменьшая размеры площадки DF до нуля (стягивая ее в точку А), получим в пределе полное напряжение в точке А.

(1.1)

Измеряются напряжения в Мпа (кгс/см²).

Проведем в плоскости сечения координатные оси x, y, а по нормали к сечению ось «z» (рис. 1.8). Находя составляющие вектора полного напряжения P вдоль осей x, y, z, получим: - нормальное напряжение (параллельно оси z); и - касательные напряжения, лежащие в плоскости сечения с нормалью z и параллельные соответствующим осям X и Y.

Выделим в окрестности точки А элементарную (бесконечно малую) площадку dF (см. рис. 1.8). Тогда между напряжениями и внутренними силовыми факторами можно установить следующие зависимости:

(1.2)

.

Если через точки А проводить секущие площадки, напряжения на этих площадках, вообще говоря, будут различными, но: совокупность всех напряжений, возникающих на различных площадках, проходящих через одну и ту же точку не изменяется и называется напряженным состоянием в точке.

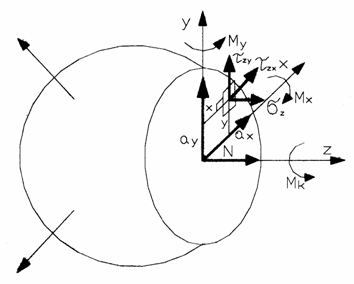
Рис. 1.8. Нормальные и касательные напряжения

1.9. Деформации. Деформированное состояние в точке

Рассмотрим малый отрезок АВ, длина которого «S» (рис.1.9). Под действием нагрузки точки А и В займут положение А₁ и В₁, а длина отрезка станет равной S+DS.

Уменьшая длину отрезка АВ до нуля, (стягивая его в точку А), получим линейную деформацию в точке А по направлению АВ.

. (1.3)

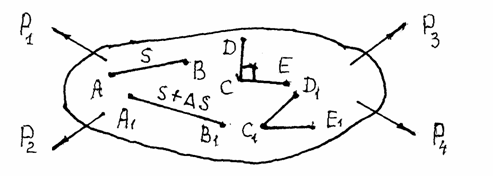
Рис.1.9. Линейные и угловые деформации

В координатных осях x, y, z линейная деформация обозначается e_x, e_y, e_z.

Рассмотрим в недеформированном теле прямой угол ДСЕ (см. рис. 1.9), который после деформации изменяется и станет равным углу Д₁С₁Е₁. Уменьшая длину отрезков СД и СЕ до нуля получим предел разности углов ДСЕ и Д₁С₁Е₁.

g_ДСЕ = Lim|LДСЕ - LД₁С₁Е₁|, (1.4.)

ДС ® 0

ЕС ® 0

который называется угловой деформацией или углом сдвига в точке С в плоскости ДСЕ. В координатных плоскостях угловая деформация обозначается g_xy, g_yz, g_zx. В зависимости от направления в пространстве отрезков АВ, СД и СЕ линейные и угловые деформации в точке будут различные, но: совокупность линейных и угловых деформаций по различным направлениям и плоскостям не изменяется и называется деформированным состоянием в точке.

1.10. Закон Гука. Принцип неизменности начальных размеров.

Принцип независимости действия сил

В 1676 г. Р. Гуком экспериментально было установлено, что в большинстве случаев перемещения пропорциональны приложенным силам.

В настоящее время закон Гука предполагает линейную зависимость между напряжениями и деформациями.

У большинства реальных конструкций перемещения и деформации настолько малы, что ими можно пренебречь при определении реакций, внутренних силовых факторов, напряжений и т.д.

В этом случае говорят, что система подчиняется принципу неизменности начальных размеров. Например, для конструкции, представленной на рис.1.10, при составлении уравнении равновесия для определения усилий в стержнях 1 и 2 можно не учитывать перемещение точки А и изменение положения стержней.

Если материал подчиняется закону Гука, а система принципу неизменности начальных размеров, то такая система называется линейно-деформируемой и для этой системы перемещения пропорциональны приложенным силам. Если материал системы не подчиняется закону Гука, то такая система физически нелинейна. Если система не подчиняется принципу неизменности начальных размеров, то такая система геометрически нелинейна.

Линейно-деформированные системы подчиняются принципу независимости действия сил (принципу суперпозиций), согласно которому действие суммы сил равно сумме действий каждой силы в отдельности. Другими словами, если на систему действуют силы Р₁, Р₁...Р_п, то реакции, внутренние силовые факторы, напряжения и т.д. можно определить, или одновременно прикладывая эти силы, или прикладывая их отдельно в любой последовательности и складывая затем полученные результаты.

1.11. Контрольные вопросы к главе 1

1.11.1. В чем состоит основная задача сопротивления материалов? Что такое прочность, жесткость, устойчивость? Основные гипотезы о материале. Что называется брусом, пластиной, оболочкой, массивом? Что такое расчетная схема? По каким причинам и как классифицируются нагрузки?

1.11.2. В чем сущность метода сечений? Какие внутренние силовые факторы могут возникать в поперечных сечениях бруса и какие виды нагружений с ним связанны?

1.11.3. Что называется полным, нормальным и касательным напряжением? Какова их размерность? Что такое напряженное состояние в точке?

1.11.4. Какие деформации называются линейными и какие угловыми? Что такое деформированное состояние в точке?

1.11.5. В чем заключается закон Гука, принцип неизменности начальных размеров и принцип независимости действия сил? Что такое линейно-деформируемые системы и какие системы называются нелинейными?

< В начало >

< Содержание >