Пример 1. Выполнение типового контрольного задания (см. раздел 1) для заданной генерирующей матрицы G.

А) Известно, что генерирующая матрица имеет размер (k x n), где k – число строк матрицы, а n – число столбцов. Скорость кода вычисляется как отношение значения k к значению n. Следовательно, длина n кода равна 4, размерность кода k равна 2, а скорость кода равна 2/4=1/2.

В) Для вычисления количества кодовых слов воспользуемся тем фактом, что двоичный (n,k)-код С любому двоичному вектору длины k ставит в соответствие одно кодовое слово длины n. Следовательно количество кодовых слов кода С совпадает с числом всех возможных двоичных векторов длины k; число таких векторов определяется как 2^k. В рассматриваемом примере число кодовых слов равно 2²=4.

C) Преобразуем матрицу G в систематический вид . Для чего переставим второй и четвертый столбцы:

таким образом, проверочная подматрица равна

Отметим, что в данном случае выполняется соотношение Р=Р^Т. Коды, у которых выполняется такое соотношение, называются самодуальными. Согласно формуле 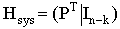запишем проверочную матрицу

D) Информационными словами u являются все возможные двоичные слова длины k=2. Кодовые слова v вычислим, используя формулу v=u?G. Отметим, что в зависимости от того, в систематическом или несистематическом виде использовать порождающую матрицу, одному и тому же информационному слово могут соответствовать различные кодовые слова. Несмотря на это полученные коды будут изоморфными.

E) Организуем таблицу размером 5 столбцов и 4 строки. Выполним шаг А процедуры построения декодирующая таблицы. А именно, запишем в заголовок таблицы все информационные слова, а в первую строку соответствующие им кодовые слова. Для выполнения этих действий воспользуемся результатами, полученными при выполнении задания D.

Для j=1 находим произвольное слово e₁IV₂ минимального веса Хемминга, не являющееся кодовым и не включенное в предыдущие строки таблицы. Пусть e₁=1000, вычисляем синдром этого вектора по формуле s=eH^T

Запишем полученный синдром s₁=11 в первый столбец второй строки. В остальных ячейках этой строки запишем суммы кодовых слов из первой строки и вектора ошибок e₁=1000.

Увеличиваем j на единицу. Для j=2 находим произвольное слово e₂IV₂ минимального веса Хемминга, не являющееся кодовым и не включенное в предыдущие строки таблицы. Пусть e₂=0100, вычисляем синдром этого вектора

Запишем полученный синдром s₂=10 в первый столбец третьей строки. В остальных ячейках этой строки запишем суммы кодовых слов из первой строки и вектора ошибок e₂=0100.

Увеличиваем j на единицу. Для j=3 находим произвольное слово e₃IV₂ минимального веса Хемминга, не являющееся кодовым и не включенное в предыдущие строки таблицы. Пусть e₃=0001, вычисляем синдром этого вектора

Запишем полученный синдром s₃=01 в первый столбец четвертой строки. В остальных ячейках этой строки запишем суммы кодовых слов из первой строки и вектора ошибок e₃=0001.

Увеличиваем j и заканчиваем построение таблицы, так как для j=4 не выполняется условие j<2^n-k.

У рассматриваемого кода 4 смежных класса, лидерами которых являются: e₀=0000, e₁=1000, e₂=0100, e₃=0001.

При построении таблицы в качестве вектора ошибок не был выбран вектор e=0010. Причина этого заключается в том, что синдром этого вектора совпадает с синдромом вектора e₂=0100, что в свою очередь происходит из-за того, что данный код является кодом с неравной защитой от ошибок, то есть число исправляемых ошибок зависит от местоположения ошибок.

F) Пусть в канал было передано кодовое слово с=0110, а из канала принято слово r=0010. Рассчитаем синдром для принятого вектора и декодируем его, используя стандартную таблицу.

По декодирующей таблице находим, что синдром s=10 находится в третьей строке. В этой же строке отыскиваем вектор r=0010. В первой строке этого же столбца находится переданное кодовое слово с=0110. Одиночная ошибка в слове исправлена. Этот факт выглядит странно, так как минимальное расстояние рассматриваемого кода равно 2, а, следовательно, исправление однократных ошибок не гарантируется. Объяснение этого факта заключается в том, что, как уже отмечалось, данный код является кодом с неравной защитой от ошибок.

G) Для вычисления способностей кода по исправлению и обнаружению ошибок вычислим минимальное расстояние Хемминга для этого кода, как минимум Хемминговых весов ненулевых кодовых слов кода С (см. раздел 2.7). Веса Хемминга кодовых слов: wt_h(0110)=2, wt_h(1011)=3, wt_h(1101)=2. Минимальное расстояние Хемминга: d_min=min{2, 3, 2}=2. Используя формулу из раздела 2.8, вычисляем, что рассматриваемый код гарантировано обнаруживает 1 ошибку, а исправляет 0 ошибок.

Пример 2. Выполнение типового контрольного задания (см. раздел 1) для заданной проверочной матрицы H.

A. Проверочная матрица Н имеет размер (n-k)? n. Следовательно, длина кода n=7, размерность кода k=n-(n-k)=7-3=4, скорость кода равна 4/7.

B. Число кодовых слов определяется как 2^k=2⁴=16.

C. Приведем матрицу H к систематическому виду. Переставим местами столбцы 2 и 6, 3 и 7.

Правые четыре столбца матрицы H_sys представляют собой транспонированную проверочную подматрицу Р. Выпишем матрицу Р:

Согласно формуле 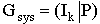запишем порождающую матрицу в систематическом виде

D. Информационными словами u являются все возможные двоичные слова длины k=4. Кодовые слова v вычислим, используя формулу v=u?G и используя матрицу G_sys.

E. Стандартная декодирующая таблица этого кода должна содержать 2^n?k=2^7?4=8 строк и 2^k+1=2⁴+1=17 столбцов. Для удобства разделим эту таблицу по ширине на две части (табл. 1), которые заполним согласно процедуре построения из раздела 2.4.

У рассматриваемого кода 8 смежных классов, лидерами которых являются: e₀=0000000, e₁=0000001, e₂=0000010, e₃=0000100, e₄=0001000, e₅=0010000, e₆=0100000, e₇=1000000.

F) Пусть в канал было передано кодовое слово с=0011001 (соответствующее информационному слову u=0011), а из канала принято слово r=1011001 (содержащее один ошибочный символ). Синдромом для r является вектор s:

В табл. 1 синдрому s=(011) соответствует строка 5, двигаясь по этой строке, отыскиваем полученный из канала вектор r=1011001 и находим соответствующее этому вектору информационное слово u=0011. Вывод: декодирование успешно.

Пусть теперь в канал было передано кодовое слово с=0011001 (соответствующее информационному слову u=0011), а из канала принято слово r=1011011 (два ошибочных символа). Вычислим синдром s:

В табл. 1 синдрому s=(111) соответствует строка 2, двигаясь по этой строке, отыскиваем полученный из канала вектор r=1011011 и находим соответствующее этому вектору кодовое слово u=1011. Вывод: декодирование неудачно.

G) Минимальное расстояние Хемминга этого кода найдем как минимум Хемминговых весов d_min=min{ wt_h(0001111)=4, wt_h(0010110)=3, wt_h(0011001)=3, wt_h(0100101)=3, wt_h(0101010)=3, wt_h(0110011)=4, wt_h(0111100)=4, wt_h(1000011)=3, wt_h(1001100)=3, wt_h(1010101)=4, wt_h(1011010)=4, wt_h(1100110)=4, wt_h(1101001)=4, wt_h(1110000)=3, wt_h(1111111)=8}=3. Следовательно, рассматриваемый код гарантировано обнаруживает две, а исправляет 1 ошибку.

Таблица 1. Часть 1

Таблица 1. Часть 2